Paper:
A Path-Following Feedback Control Law of a Five-Axle, Three-Steering Coupled-Vehicle System
Hiroaki Yamaguchi*, Ryota Kameyama*,**, and Atsushi Kawakami*
*Department of Integrated Information Technology, College of Science and Engineering, Aoyama Gakuin University, 5-10-1 Fuchinobe, Chuo-ku, Sagamihara-shi, Kanagawa 252-5258, Japan
**Rolling Stock Electrical Systems Design Department, Mito Rail Systems Product Division, Rail Systems Company, Hitachi, Ltd., 1070 Ichige, Hitachinaka-shi, Ibaraki 312-8506, Japan
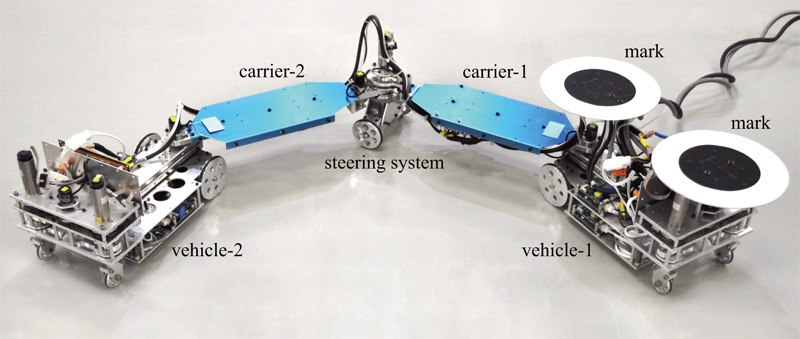 Experimental coupled-vehicle system
Experimental coupled-vehicle system- [1] Z. P. Jiang and H. Nijmeijer, “A Recursive Technique for Tracking Control of Nonholonomic Systems in Chained Form,” IEEE Trans. on Automatic Control, Vol.44, No.2, pp. 265-279, 1999.
- [2] F. Lamiraux, S. Sekhavat, and J. P. Laumond, “Motion Planning and Control for Hilare Pulling a Trailer,” IEEE Trans. on Robotics and Automation, Vol.15, No.4, pp. 640-652, 1999.
- [3] J.-P. Laumond, “Controllability of a Multibody Mobile Robot,” IEEE Trans. on Robotics and Automation, Vol.9, No.6, pp. 755-763, 1993.
- [4] W. Li, T. Tsubouchi, and S. Yuta, “Manipulative Difficulty of a Mobile Robot Pushing and Towing Multiple Trailers,” Advanced Robotics, Vo.14, No.3, pp. 169-183, 2000.
- [5] P. Rouchon, M. Fliess, J. Levine, and P. Martin, “Flatness, Motion Planning and Trailer Systems,” Proc. of the 32nd IEEE Conf. on Decision and Control, Vol.3, pp. 2700-2705, 1993.
- [6] M. Sampei, T. Tamura, T. Kobayashi, and N. Shibui, “Arbitrary Path Tracking Control of Articulated Vehicles Using Nonlinear Control Theory,” IEEE Trans. on Control Systems Technology, Vol.3, No.1, pp. 125-131, 1995.
- [7] C. Samson, “Control of Chained Systems: Application to Path Following and Time-varying Point-Stabilization of Mobile Robots,” IEEE Trans. on Automatic Control, Vol.40, No.1, pp. 64-77, 1995.
- [8] S. Sekhavat and J.-P. Laumond, “Topological Property for Collision-Free Nonholonomic Motion Planning: The Case of Sinusoidal Inputs for Chained Form Systems,” IEEE Trans. on Robotics and Automation, Vol.14, No.5, pp. 671-680, 1998.
- [9] Y. Sklyarenko, F. Schreiber, andW. Schumacher, “Maneuvering Assistant for Truck and Trailer Combinations with Arbitrary Trailer Hitching,” Proc. of the 2013 IEEE Int. Conf. on Mechatronics, pp. 774-779, 2013.
- [10] O. J. Sordalen, “Conversion of the Kinematics of a Car with N Trailers into a Chained Form,” Proc. of the 1993 IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 382-387, 1993.
- [11] O. J. Sordalen and K. Y. Wichlund, “Exponential Stabilization of a Car with N Trailers,” Proc. of the 32nd IEEE Conf. on Decision and Control, Vol.2, pp. 978-983, 1993.
- [12] D. M. Tilbury, R. M. Murray, and S. S. Sastry, “Trajectory Generation for the N-trailer Problem Using Goursat Normal Form,” IEEE Trans. on Automatic Control, Vol.40, No.5, pp. 802-819, 1995.
- [13] C. Altafini, “Some Properties of the General N-Trailer,” Int. J. of Control, Vol.74, No.4, pp.409-424, 2001.
- [14] C. Altafini, “Path Following with Reduced Off-Tracking for MultibodyWheeled Vehicles,” IEEE Trans. on Control Systems Technology, Vol.11, No.4, pp. 598-605, 2003.
- [15] P. Bolzern, R. M. DeSantis, A. Locatelli, and D.Masciocchi, “Path-Tracking for Articulated Vehicles with Off-Axle Hitching,” IEEE Trans. on Control Systems Technology, Vol.6, No.4, pp. 515-523, 1998.
- [16] L. G. Bushnell, “An Obstacle Avoidance Algorithm for a Car Pulling Trailers with Off-axle Hitching,” Proc. of the 34th IEEE Conf. on Decision and Control, Vol.4, pp. 3837-3842, 1995.
- [17] R. M. Desantis, J. M. Bourgeot, J. N. Todeschi, and R. Hurteau, “Path-tracking for Tractor-trailers with Hitching of Both the Onaxle and the Off-axle Kind,” Proc. of the 2002 IEEE Int. Symposium on Intelligent Control, pp. 206-211, 2002.
- [18] F. Lamiraux, D. Bonnafous and O. Lefebvre, “Reactive Path Deformation for Nonholonomic Mobile Robots,” IEEE Trans. on Robotics, Vol.20, No.6, pp. 967-977, 2004.
- [19] D. A. Lizarraga, P.Morin, and C. Samson, “Chained Form Approximation of a Driftless System. Application to the Exponential Stabilization of the General N-Trailer System,” Int. J. of Control, Vo.74, No.16, pp. 1612-1629, 2001.
- [20] K. Matsushita and T. Murakami, “Nonholonomic Equivalent Disturbance Based Backward Motion Control of Tractor-Trailer with Virtual Steering,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 280-287, 2008.
- [21] P. Morin and C. Samson, “Feedback Control of the General Twotrailers System with the Transverse Function Approach,” Proc. of the 51st IEEE Conf. on Decision and Control (CDC 2012), pp. 1003-1010, 2012.
- [22] M. Vendittelli, G. Oriolo, and J.-P. Laumond, “Steering Nonholonomic Systems via Nilpotent Approximations: the General Twotrailer System,” Proc. of the 1999 IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 823-829, 1999.
- [23] M. Vendittelli and G. Oriolo, “Stabilization of the General Twotrailer System,” Proc. of the 2000 IEEE Int. Conf. on Robotics and Automation, Vol.2, pp. 1817-1823, 2000.
- [24] L. G. Bushnell, D. M. Tilbury, and S. S. Sastry, “Steering Three-Input Nonholonomic Systems: The Fire Truck Example,” Int. J. of Robotics Research, Vol.14, No.4, pp. 366-381, 1995.
- [25] F. Lamiraux, J.-P. Laumond, C. Van Geem, D. Boutonnet, and G. Raust, “Trailer Truck Trajectory Optimization: The Transportation of Components for the Airbus A380,” IEEE Robotics and Automation Magazine, Vol.12, No.1, pp. 14-21, 2005.
- [26] Y. Nakamura, H. Ezaki, Y. Tan, and W. Chung, “Design of Steering Mechanism and Control of Nonholonomic Trailer Systems,” IEEE Trans. on Robotics and Automation, Vol.17, No.3, pp. 367-374, 2001.
- [27] D. M. Tilbury, O. J. Sordalen, L. G. Bushnell, and S. S. Sastry, “A multisteering Trailer System: Conversion into Chained Form Using Dynamic Feedback,” IEEE Trans. on Robotics and Automation, Vol.11, No.6, pp. 807-818, 1995.
- [28] D. M. Tilbury and S. S. Sastry, “The Multi-Steering N-Trailer System: A Case Study of Goursat Normal Forms and Prolongations,” Int. J. of Robust and Nonlinear Control, Vol.5, No.4, pp. 343-364, 1995.
- [29] H. Yamaguchi and T. Arai, “A Path Following Feedback Control Method for a Cooperative Transportation System with Two Car-Like Mobile Robots,” Trans. of the Society of Instrument and Control Engineers, Vol.39, No.6, pp. 575-584, 2003 (in Japanese).
- [30] H. Yamaguchi, M. Mori, and A. Kawakami, “A Path Following Feedback Control Method Using Parametric Curves for a Cooperative Transportation System with Two Car-Like Mobile Robots,” Proc. of the 7th IFAC Symposium on Intelligent Autonomous Vehicles, pp. 163-168, 2010.
- [31] H. Yamaguchi, M. Mori, and A. Kawakami, “Control of a Five-Axle, Three-Steering Coupled-Vehicle System,” Trans. of the Society of Instrument and Control Engineers, Vol.46, No.6, pp. 317-326, 2010 (in Japanese).
- [32] H. Yamaguchi, M. Mori, and A. Kawakami, “Control of a Five-Axle, Three-Steering Coupled-Vehicle System and Its Experimental Verification,” Proc. of the 18th IFACWorld Congress, Vol.18, No.1, pp. 12976-12984, 2011.
- [33] A. Isidori, “Nonlinear Control Systems,” New York: Springer-Verlag, Second Edition, 1989.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.