Paper:
3-1 Piecewise NCP Function for New Nonmonotone QP-Free Infeasible Method
Ailan Liu*,** and Dingguo Pu*,***
*Department of Mathematics, Tongji University, No.1239, Siping Road, Shanghai 200092, China
**School of Mathematics and Physics, Shanghai University of Electric Power, No.2588, Changyang Road, Yangpu District, Shanghai, China
***School of Mathematics and Statistics, Henan University of Science and Technology, No.263, Kaiyuan Road, Luoyang 471023, China
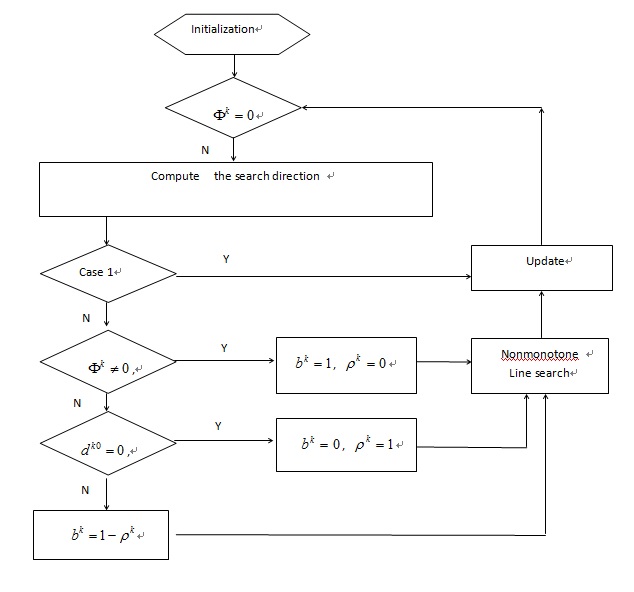 Algorithm flow chart
Algorithm flow chart- [1] M. Yokozuka and O. Matsumoto, “A reasonable path planning via path energy minimization,” J. of Robotics and Mechatronics, Vol.26, No.2, pp. 236-244, 2014.
- [2] C. H. Kim, H. Tsujino, and S. Sugano, “Rapid short-time path planning for phase space,” J. of Robotics and Mechatronics, Vol.23, No.2, pp. 271-280. 2011.
- [3] P. Di, J. Huang, S. Nakagawa et al., “Optimized motion control of an intelligent cane robot for easing muscular fatigue in the elderly during walking,” J. of Robotics and Mechatronics, Vol.25, No.6, pp. 1070-1077. 2013.
- [4] N. I. M. Gould and P. L. Toint, “Nonlinear programming without a penalty function and a filter,” Math. Program., Vol.122, pp. 155-196, 2010.
- [5] X. W. Liu and Y. X. Yuan, “A sequential quadratic programming method a penalty function and a filter for equality constrained nonlinear programming,” SIAM J. on Optimization, Vol.21, No.2, pp. 545-571, 2011.
- [6] D. G. Pu, A. L. Liu, Y. L. Shang et al., “QP-free infeasible method without a penalty function and a filter,” Operations Research Trans., Vol.17, No.1, pp. 106-116, 2013.
- [7] Y. Zhou and D. G. Pu, “Piecewise linear NCP function for QP-free feasible method,” J. Appl. Math., Vol.21, No.3, pp. 289-301, 2006.
- [8] H. D. Qi and L. Q. Qi, “A new QP-free, globally convergent, locally superlinearly convergent algorithm for inequality constrained optimization,” SIAM J Optim, Vol.11, pp. 113-132, 2000.
- [9] L. Q. Qi and Y. F. Yang, “A globally and superlinearly convergent QP-free for nonlinear constrained optimization,” J. Optim. Theory Appl., Vol.113, pp. 297-323, 2002.
- [10] Z. B. Zhu and J. B. Jin, “An improved feasible QP-free algorithm for inequality constrained optimization,” Acta. Math. Sinica, Vol.28, No.12, pp. 2475-2488, 2012.
- [11] E. R. Panier, A. L. Tits, and J. N. Herskovits, “A QP-free, globally, locally superlinear convergent method for the inequality constrained optimization problems,” SIAM J. Control Optim., Vol.36, pp. 788-811, 1988.
- [12] M. Ulbrich and S. Ulbrich, “Non-monotone trust region methods for nonlinear equality constrained optimization without a penalty function,” Math Program, Vol.95, pp. 103-135, 2003.
- [13] W. Hock and K. Schittkowski, “Test examples for nonlinear programming codesLecture Notes in Economics and Mathematical Systems,” Vol.187, Springer-Verlag, Berlin Heidelberg New York, 1981.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.