Top > JRM > A Path-Following Feedback Control Law of a Five-Axle, Three-St ...

single-rb.php

JRM Vol.26 No.5 pp. 551-565
doi: 10.20965/jrm.2014.p0551
(2014)

Paper:

Views over last 60 days: 1,056

A Path-Following Feedback Control Law of a Five-Axle, Three-Steering Coupled-Vehicle System

Hiroaki Yamaguchi*, Ryota Kameyama*,**, and Atsushi Kawakami*

*Department of Integrated Information Technology, College of Science and Engineering, Aoyama Gakuin University, 5-10-1 Fuchinobe, Chuo-ku, Sagamihara-shi, Kanagawa 252-5258, Japan

**Rolling Stock Electrical Systems Design Department, Mito Rail Systems Product Division, Rail Systems Company, Hitachi, Ltd., 1070 Ichige, Hitachinaka-shi, Ibaraki 312-8506, Japan

Received:
September 27, 2013
Accepted:
June 6, 2014
Published:
October 20, 2014
Creative Commons License
Keywords:
nonholonomic system, chained form, coupled-vehicle system, path-following, Lyapunov’s second method
Abstract
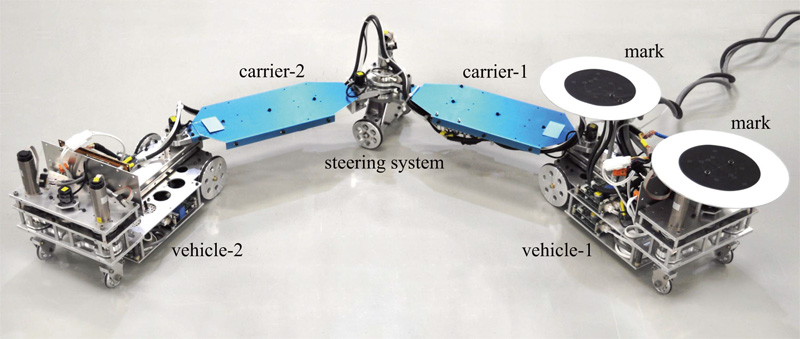Experimental coupled-vehicle system
This paper presents a new path-following feedback control law of a five-axle, three-steering coupledvehicle system which enables specifying the movements and rotations of its two carriers quantitatively, according to the operating environment. The kinematical equations of the coupled-vehicle system are first converted into time differential equations in a threechain, single-generator chained form. The time differential equations in the chained form are secondly converted into new differential equations with a new variable. The new control law enables the relative orientation between the two carriers to be constant in either a straight-bed carrier configuration or a V-bed carrier configuration, and simultaneously enables the orientations of these carriers functioning as a single carrier relative to the direction of the tangent of the path to be changed quantitatively, according to the locations of obstacles for avoiding collision with them. Asymptotic stability of the new control law is guaranteed by the linear control theory and the Lyapunov’s second method. Especially, the form of the new differential equations facilitates the design of the Lyapunov functions. The validity of the new control law is verified by an experimental five-axle, three-steering coupledvehicle system.
Cite this article as:
H. Yamaguchi, R. Kameyama, and A. Kawakami, “A Path-Following Feedback Control Law of a Five-Axle, Three-Steering Coupled-Vehicle System,” J. Robot. Mechatron., Vol.26 No.5, pp. 551-565, 2014.
Data files:
References
  1. [1] Z. P. Jiang and H. Nijmeijer, “A Recursive Technique for Tracking Control of Nonholonomic Systems in Chained Form,” IEEE Trans. on Automatic Control, Vol.44, No.2, pp. 265-279, 1999.
  2. [2] F. Lamiraux, S. Sekhavat, and J. P. Laumond, “Motion Planning and Control for Hilare Pulling a Trailer,” IEEE Trans. on Robotics and Automation, Vol.15, No.4, pp. 640-652, 1999.
  3. [3] J.-P. Laumond, “Controllability of a Multibody Mobile Robot,” IEEE Trans. on Robotics and Automation, Vol.9, No.6, pp. 755-763, 1993.
  4. [4] W. Li, T. Tsubouchi, and S. Yuta, “Manipulative Difficulty of a Mobile Robot Pushing and Towing Multiple Trailers,” Advanced Robotics, Vo.14, No.3, pp. 169-183, 2000.
  5. [5] P. Rouchon, M. Fliess, J. Levine, and P. Martin, “Flatness, Motion Planning and Trailer Systems,” Proc. of the 32nd IEEE Conf. on Decision and Control, Vol.3, pp. 2700-2705, 1993.
  6. [6] M. Sampei, T. Tamura, T. Kobayashi, and N. Shibui, “Arbitrary Path Tracking Control of Articulated Vehicles Using Nonlinear Control Theory,” IEEE Trans. on Control Systems Technology, Vol.3, No.1, pp. 125-131, 1995.
  7. [7] C. Samson, “Control of Chained Systems: Application to Path Following and Time-varying Point-Stabilization of Mobile Robots,” IEEE Trans. on Automatic Control, Vol.40, No.1, pp. 64-77, 1995.
  8. [8] S. Sekhavat and J.-P. Laumond, “Topological Property for Collision-Free Nonholonomic Motion Planning: The Case of Sinusoidal Inputs for Chained Form Systems,” IEEE Trans. on Robotics and Automation, Vol.14, No.5, pp. 671-680, 1998.
  9. [9] Y. Sklyarenko, F. Schreiber, andW. Schumacher, “Maneuvering Assistant for Truck and Trailer Combinations with Arbitrary Trailer Hitching,” Proc. of the 2013 IEEE Int. Conf. on Mechatronics, pp. 774-779, 2013.
  10. [10] O. J. Sordalen, “Conversion of the Kinematics of a Car with N Trailers into a Chained Form,” Proc. of the 1993 IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 382-387, 1993.
  11. [11] O. J. Sordalen and K. Y. Wichlund, “Exponential Stabilization of a Car with N Trailers,” Proc. of the 32nd IEEE Conf. on Decision and Control, Vol.2, pp. 978-983, 1993.
  12. [12] D. M. Tilbury, R. M. Murray, and S. S. Sastry, “Trajectory Generation for the N-trailer Problem Using Goursat Normal Form,” IEEE Trans. on Automatic Control, Vol.40, No.5, pp. 802-819, 1995.
  13. [13] C. Altafini, “Some Properties of the General N-Trailer,” Int. J. of Control, Vol.74, No.4, pp.409-424, 2001.
  14. [14] C. Altafini, “Path Following with Reduced Off-Tracking for MultibodyWheeled Vehicles,” IEEE Trans. on Control Systems Technology, Vol.11, No.4, pp. 598-605, 2003.
  15. [15] P. Bolzern, R. M. DeSantis, A. Locatelli, and D.Masciocchi, “Path-Tracking for Articulated Vehicles with Off-Axle Hitching,” IEEE Trans. on Control Systems Technology, Vol.6, No.4, pp. 515-523, 1998.
  16. [16] L. G. Bushnell, “An Obstacle Avoidance Algorithm for a Car Pulling Trailers with Off-axle Hitching,” Proc. of the 34th IEEE Conf. on Decision and Control, Vol.4, pp. 3837-3842, 1995.
  17. [17] R. M. Desantis, J. M. Bourgeot, J. N. Todeschi, and R. Hurteau, “Path-tracking for Tractor-trailers with Hitching of Both the Onaxle and the Off-axle Kind,” Proc. of the 2002 IEEE Int. Symposium on Intelligent Control, pp. 206-211, 2002.
  18. [18] F. Lamiraux, D. Bonnafous and O. Lefebvre, “Reactive Path Deformation for Nonholonomic Mobile Robots,” IEEE Trans. on Robotics, Vol.20, No.6, pp. 967-977, 2004.
  19. [19] D. A. Lizarraga, P.Morin, and C. Samson, “Chained Form Approximation of a Driftless System. Application to the Exponential Stabilization of the General N-Trailer System,” Int. J. of Control, Vo.74, No.16, pp. 1612-1629, 2001.
  20. [20] K. Matsushita and T. Murakami, “Nonholonomic Equivalent Disturbance Based Backward Motion Control of Tractor-Trailer with Virtual Steering,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 280-287, 2008.
  21. [21] P. Morin and C. Samson, “Feedback Control of the General Twotrailers System with the Transverse Function Approach,” Proc. of the 51st IEEE Conf. on Decision and Control (CDC 2012), pp. 1003-1010, 2012.
  22. [22] M. Vendittelli, G. Oriolo, and J.-P. Laumond, “Steering Nonholonomic Systems via Nilpotent Approximations: the General Twotrailer System,” Proc. of the 1999 IEEE Int. Conf. on Robotics and Automation, Vol.1, pp. 823-829, 1999.
  23. [23] M. Vendittelli and G. Oriolo, “Stabilization of the General Twotrailer System,” Proc. of the 2000 IEEE Int. Conf. on Robotics and Automation, Vol.2, pp. 1817-1823, 2000.
  24. [24] L. G. Bushnell, D. M. Tilbury, and S. S. Sastry, “Steering Three-Input Nonholonomic Systems: The Fire Truck Example,” Int. J. of Robotics Research, Vol.14, No.4, pp. 366-381, 1995.
  25. [25] F. Lamiraux, J.-P. Laumond, C. Van Geem, D. Boutonnet, and G. Raust, “Trailer Truck Trajectory Optimization: The Transportation of Components for the Airbus A380,” IEEE Robotics and Automation Magazine, Vol.12, No.1, pp. 14-21, 2005.
  26. [26] Y. Nakamura, H. Ezaki, Y. Tan, and W. Chung, “Design of Steering Mechanism and Control of Nonholonomic Trailer Systems,” IEEE Trans. on Robotics and Automation, Vol.17, No.3, pp. 367-374, 2001.
  27. [27] D. M. Tilbury, O. J. Sordalen, L. G. Bushnell, and S. S. Sastry, “A multisteering Trailer System: Conversion into Chained Form Using Dynamic Feedback,” IEEE Trans. on Robotics and Automation, Vol.11, No.6, pp. 807-818, 1995.
  28. [28] D. M. Tilbury and S. S. Sastry, “The Multi-Steering N-Trailer System: A Case Study of Goursat Normal Forms and Prolongations,” Int. J. of Robust and Nonlinear Control, Vol.5, No.4, pp. 343-364, 1995.
  29. [29] H. Yamaguchi and T. Arai, “A Path Following Feedback Control Method for a Cooperative Transportation System with Two Car-Like Mobile Robots,” Trans. of the Society of Instrument and Control Engineers, Vol.39, No.6, pp. 575-584, 2003 (in Japanese).
  30. [30] H. Yamaguchi, M. Mori, and A. Kawakami, “A Path Following Feedback Control Method Using Parametric Curves for a Cooperative Transportation System with Two Car-Like Mobile Robots,” Proc. of the 7th IFAC Symposium on Intelligent Autonomous Vehicles, pp. 163-168, 2010.
  31. [31] H. Yamaguchi, M. Mori, and A. Kawakami, “Control of a Five-Axle, Three-Steering Coupled-Vehicle System,” Trans. of the Society of Instrument and Control Engineers, Vol.46, No.6, pp. 317-326, 2010 (in Japanese).
  32. [32] H. Yamaguchi, M. Mori, and A. Kawakami, “Control of a Five-Axle, Three-Steering Coupled-Vehicle System and Its Experimental Verification,” Proc. of the 18th IFACWorld Congress, Vol.18, No.1, pp. 12976-12984, 2011.
  33. [33] A. Isidori, “Nonlinear Control Systems,” New York: Springer-Verlag, Second Edition, 1989.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Apr. 18, 2024