Paper:
Fuzzy Clustering Method for Spherical Data Based on q-Divergence
Masayuki Higashi, Tadafumi Kondo, and Yuchi Kanzawa
Shibaura Institute of Technology
3-7-5 Toyosu, Koto, Tokyo 135-8548, Japan
This study presents a fuzzy clustering algorithm for classifying spherical data based on q-divergence. First, it is shown that a conventional method for vectorial data is equivalent to the regularization of another conventional method using q-divergence. Next, based on the knowledge that q-divergence is a generalization of Kullback-Leibler (KL)-divergence and that there is a conventional fuzzy clustering method for classifying spherical data based on KL-divergence, a fuzzy clustering algorithm for spherical data is derived based on q-divergence. This algorithm uses an optimization problem built by extending KL-divergence in the conventional method to q-divergence. Finally, some numerical experiments are conducted to verify the proposed methods.
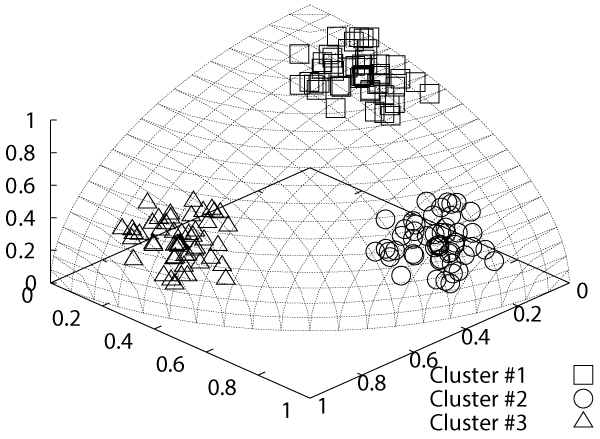
Fuzzy clustering for spherical data
- [1] J. B. MacQueen, “Some Methods for Classification and Analysis of Multivariate Observations,” Proc. 5th Berkeley Symp. on Math. Stat. and Prob., pp. 281-297, 1967.
- [2] J. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, New York, 1981.
- [3] S. Miyamoto and M. Mukaidono, “Fuzzy c-Means as a Regularization and Maximum Entropy Approach,” Proc. 7th Int. Fuzzy Systems Association World Congress (IFSA’97), Vol.2, pp. 86-92, 1997.
- [4] S. Miyamoto and N. Kurosawa, “Controlling Cluster Volume Sizes in Fuzzy c-means Clustering,” Proc. SCIS&ISIS2004, pp. 1-4, 2004.
- [5] H. Ichihashi, K. Honda, and N. Tani, “Gaussian Mixture PDF Approximation and Fuzzy c-means Clustering with Entropy Regularization,” Proc. 4th Asian Fuzzy System Symp., pp. 217-221, 2000.
- [6] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering,” Springer, 2008.
- [7] I. S. Dhillon and D. S. Modha, “Concept Decompositions for Large Sparse Text Data Using Clustering,” Machine Learning, Vol.42, pp. 143-175, 2001.
- [8] S. Miyamoto and K. Mizutani, “Fuzzy Multiset Model and Methods of Nonlinear Document Clustering for Information Retrieval,” Lecture Notes in Computer Science (LNCS), Vol.3131, pp. 273-283, 2004.
- [9] H. Chernoff, “A Measure of Asymptotic Efficiency for Tests of a Hypothesis Based on a Sum of Observations,” Ann. Math. Statist., Vol.23, pp. 493-507, 1952.
- [10] S. Miyamoto and K. Umayahara, “Methods in Hard and Fuzzy Clustering,” Z.-Q. Liu and S. Miyamoto (Eds.), Soft Computing and Human-Centered Machines, Springer-Verlag, Tokyo, 2000.
- [11] Lise’s Inquisitive Students, Machine Learning Research Group @UMD, http://www.cs.umd.edu/sen/lbc-proj/LBC.html [accessed February 10, 2017]
- [12] V. Tunali, PRETO Data Mining Research, http://www.dataminingresearch.com/ [accessed February 7, 2017]
- [13] G. Karypis, Karypis Lab, CLUTO – Software for Clustering High-Dimensional Datasets, http://glaros.dtc.umn.edu/ [accessed February 8, 2017]
- [14] Text REtrieval Conf. (TREC), http://trec.nist.gov [accessed February 10, 2017]
- [15] TREC: Text REtrieval Conf. Relevance Judgments, http://trec.nist.gov/data/qrels_eng/index.html [accessed February 8, 2017]
- [16] D. Boley, M. Gini, R. Gross, E. H. Han, K. Hastings, G. Karypis, V. Kumar, B. Mobasher, and J. Moore, “Partitioning-based clustering for web document categorization,” Decision Support Systems, Vol.27, No.3, pp. 329-341, 1999.
- [17] D. D. Lewis, Reuters-21578 text categorization test collection distribution 1.0, http://www.daviddlewis.com/resources/testcollections/reuters21578/ [accessed February 15, 2017]
- [18] W. Hersh, C. Buckley, T. J. Leone, and D. Hickam, “OHSUMED: an interactive retrieval evaluation and new large test collection for research,” Proc. SIGIR94, pp. 192-201, 1994.
- [19] L. Hubert and P. Arabie, “Comparing Partitions,” J. of Classification, Vol.2, pp. 193-218, 1985.
- [20] R. Krishnapuram and J. M. Keller, “A Possibilistic Approach to Clustering,” IEEE Trans. Fuzzy Syst., Vol.1, pp. 98-110, 1993.
- [21] Y. Kanzawa, “On Possibilistic Clustering Methods Based on Shannon/Tsallis-Entropy for Spherical Data and Categorical Multivariate Data,” Lecture Notes in Artificial Intelligence, Vol.9321, pp. 115-128, 2015.
- [22] A. Cichocki and S. Amari, “Families of Alpha- Beta- and Gamma- Divergences: Flexible and Robust Measures of Similarities,” Entropy, Vol.12, pp. 1532-1568, 2010.
- [23] A. Cichocki, S. Cruces, and S. Amari, “Generalized Alpha-Beta Divergences and Their Application to Robust Nonnegative Matrix Factorization,” Entropy, Vol.13, pp. 134-170, 2011.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.