Paper:
Kernel Fuzzy c-Regression Based on Least Absolute Deviation with Modified Huber Function
Yusuke Oi* and Yasunori Endo**
*Department of Risk Engineering, Graduate School of Systems and Information Engineering, University of Tsukuba
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan
**Faculty of Engineering, Information and Systems, University of Tsukuba
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan
The fuzzy c-regression models are useful for datasets with various correlations. To deal with nonlinear datasets, a kernel fuzzy c-regression (KFCR) method was previously proposed. However, this method is weak for outliers because its objective function is based on the least square principle. We introduce the least absolute deviation (LAD) method with a modified Huber function into the KFCR (LAD-KFCR) to overcome the abovementioned problem. We verify the usefulness of the proposed LAD-KFCR method through numerical examples.
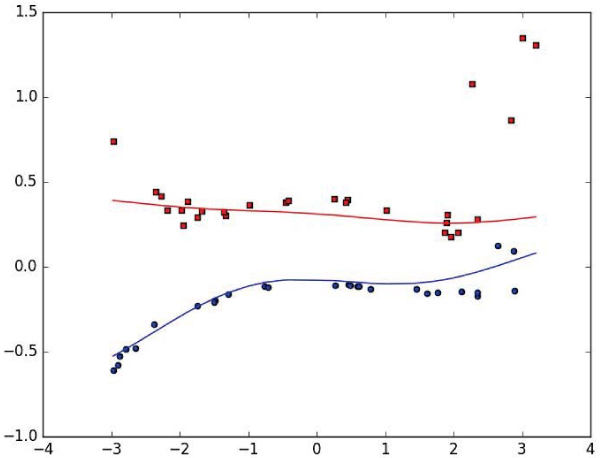
A result by the proposed method
- [1] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Springer, 1981.
- [2] R. J. Hathaway and J. C. Bezdek, “Switching Regression Models and Fuzzy Clustering,” IEEE Trans. on Fuzzy Systems, Vol.1, Issue 3, pp. 195-204, 1993.
- [3] T. Higuchi and S. Miyamoto, “Fuzzy c-Regression Models Combined with Support Vector Regression,” Proc. of 2014 IEEE Int. Conf. on Fuzzy System (FUZZ-IEEE 2014), pp. 2489-2493, 2014.
- [4] H. Tang, S. Miyamoto, and Y. Endo, “Semi-Supervised Sequential Kernel Regression Models with Penalty Functions,” J. Adv. Comput. Intell. Intell. Inform., Vol.19, No.1, pp. 51-57, 2015.
- [5] Y. Endo, K. Kurihara, S. Miyamoto, and Y. Hamasuna, “Hard and Fuzzy c-Regression Models for Data with Tolerance in Independent Dependent Variables,” Proc. of 2010 IEEE Int. Conf. on Fuzzy System (FUZZ-IEEE 2010), pp. 1842-1849, 2010.
- [6] S. Miyamoto and K. Arai, “Different Sequential Clustering Algorithms and Sequential Regression Models,” Proc. of 2009 IEEE Int. Conf. on Fuzzy System (FUZZ-IEEE 2009), pp. 1107-1112, 2009.
- [7] J. C. Dunn, “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters,” J. of Cybernetics, pp. 32-57, 1973.
- [8] K. Wang, J. Zhang, Y. Chen, and P. Zhong, “Least Absolute Deviation Support Vector Regression,” Mathematical Problems in Engineering, Vol.2014, Article ID 169575, 2014.
- [9] V. Vapnik, “The Nature of Statistical Learning Theory,” Springer, 2000.
- [10] L. Hubert and P. Arabie, “Comparing Partitions,” J. of Classification, Vol.2, Issue 1, pp. 193-218, 1985.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.