Top > JRM > Variable-Corner Robotic Surfaces with Minimal Area and Their K ...

single-rb.php

JRM Vol.37 No.1 pp. 143-152
doi: 10.20965/jrm.2025.p0143
(2025)

Paper:

Views over last 60 days: 57

Variable-Corner Robotic Surfaces with Minimal Area and Their Kinematics

Masaru Miyajima, Takuya Umedachi ORCID Icon, and Noriyasu Iwamoto ORCID Icon

Faculty of Textile Science and Technology, Shinshu University
3-15-1 Tokida, Ueda, Nagano 386-8567, Japan

Received:
August 2, 2024
Accepted:
November 8, 2024
Published:
February 20, 2025
Creative Commons License
Keywords:
robotic surfaces, soft robots, kinematics, minimal surface
Abstract

Actuators and robots capable of representing surfaces can take various forms, depending on the types of actuators used and their arrangements. In traditional robotic surfaces, the corners on the boundary in the undeformed state remain unchanged, indicating that the number and position of the boundary corners do not vary during deformation. This paper introduces a ring-shaped actuator with three types of bending elements combined with a soap film, demonstrating the existence of robotic surfaces in which the number of boundary corners can change through actuation. We also propose forward and inverse kinematics applicable to such robotic surfaces and present simulation results. These findings suggest that inverse kinematics can be achieved in soft robots constructed with prestressed silicone rubber or fabric, including membrane-like components, stretched over a frame.

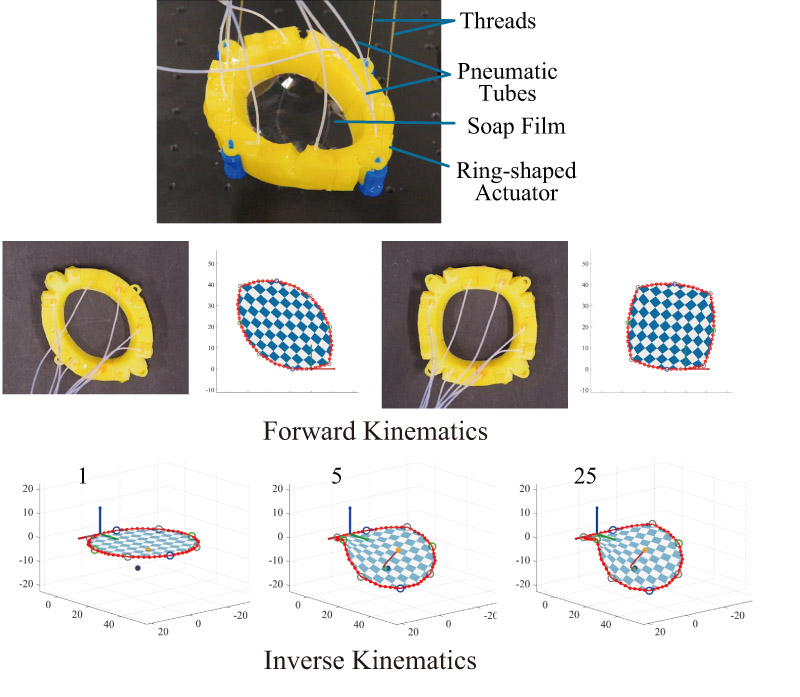
Variable-corner robotic surface and its forward and inverse kinematics

Variable-corner robotic surface and its forward and inverse kinematics

Cite this article as:
M. Miyajima, T. Umedachi, and N. Iwamoto, “Variable-Corner Robotic Surfaces with Minimal Area and Their Kinematics,” J. Robot. Mechatron., Vol.37 No.1, pp. 143-152, 2025.
Data files:
References
  1. [1] M. Cianchetti, T. Ranzani, G. Gerboni, I. De Falco, C. Laschi, and A. Menciassi, “STIFF-FLOP surgical manipulator: Mechanical design and experimental characterization of the single module,” 2013 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 3576-3581, 2013. https://doi.org/10.1109/IROS.2013.6696866
  2. [2] F. Renda, M. Giorelli, M. Calisti, M. Cianchetti, and C. Laschi, “Dynamic model of a multibending soft robot arm driven by cables,” IEEE Trans. on Robotics, Vol.30, Issue 5, pp. 1109-1122, 2014. https://doi.org/10.1109/TRO.2014.2325992
  3. [3] P. E. Dupont, J. Lock, B. Itkowitz, and E. Butler, “Design and control of concentric-tube robots,” IEEE Trans. on Robotics, Vol.26, Issue 2, pp. 209-225, 2009. https://doi.org/10.1109/TRO.2009.2035740
  4. [4] T. Nakamura, “Fluid-Driven Soft Actuators for Soft Robots,” J. Robot. Mechatron., Vol.36, No.2, pp. 251-259, 2024. https://doi.org/10.20965/jrm.2024.p0251
  5. [5] K. Tadakuma, M. Kawakami, and H. Furukawa, “From a Deployable Soft Mechanism Inspired by a Nemertea Proboscis to a Robotic Blood Vessel Mechanism,” J. Robot. Mechatron., Vol.34, No.2, pp. 234-239, 2022. https://doi.org/10.20965/jrm.2022.p0234
  6. [6] R. J. Webster III and B. A. Jones, “Design and kinematic modeling of constant curvature continuum robots: A review,” The Int. J. of Robotics Research, Vol.29, Issue 13, pp. 1661-1683, 2010. https://doi.org/10.1177/0278364910368147
  7. [7] S. Follmer, D. Leithinger, A. Olwal, N. Cheng, and H. Ishii, “Jamming User Interfaces: Programmable Particle Stiffness and Sensing for Malleable and Shape-Changing Devices,” Proc. of the 25th Annual ACM Symp. on User Interface Software and Technology (UIST ’12), pp. 519-528, 2012. https://doi.org/10.1145/2380116.2380181
  8. [8] A. A. Stanley and A. M. Okamura, “Controllable surface haptics via particle jamming and pneumatics,” IEEE Trans. on Haptics, Vol.8, Issue 1, pp. 20-30, 2015. https://doi.org/10.1109/TOH.2015.2391093
  9. [9] A. A. Stanley, K. Hata, and A. M. Okamura, “Closed-loop shape control of a haptic jamming deformable surface,” 2016 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 2718-2724, 2016. https://doi.org/10.1109/ICRA.2016.7487433
  10. [10] A. A. Stanley and A. M. Okamura, “Deformable model-based methods for shape control of a haptic jamming surface,” IEEE Trans. on Visualization and Computer Graphics, Vol.23, Issue 2, pp. 1029-1041, 2016. https://doi.org/10.1109/TVCG.2016.2525788
  11. [11] H. Habibi, C. Yang, I. S. Godage, R. Kang, I. D. Walker, and D. T. Branson III, “A lumped-mass model for large deformation continuum surfaces actuated by continuum robotic arms,” J. of Mechanisms and Robotics, Vol.12, Issue 1, Article No.011014, 2020. https://doi.org/10.1115/1.4045037
  12. [12] Y. Funabora, “Prototype of a fabric actuator with multiple thin artificial muscles for wearable assistive devices,” 2017 IEEE/SICE Int. Symp. on System Integration (SII), pp. 356-361, 2017. https://doi.org/10.1109/SII.2017.8279238
  13. [13] E. Steltz, A. Mozeika, N. Rodenberg, E. Brown, and H. M. Jaeger, “JSEL: Jamming skin enabled locomotion,” 2009 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 5672-5677, 2009. https://doi.org/10.1109/IROS.2009.5354790
  14. [14] C. Freeman, M. Maynard, and V. Vikas, “Topology and Morphology Design of Spherically Reconfigurable Homogeneous Modular Soft Robots,” Soft Robotics, Vol.10, No.1, pp. 52-65, 2023. https://doi.org/10.1089/soro.2021.0125
  15. [15] H. Kimura, M. Kataoka, and N. Inou, “Hermetically-Sealed Flexible Mobile Robot “MOLOOP” for Narrow Terrain Exploration,” J. Robot. Mechatron., Vol.34, No.2, pp. 361-372, 2022. https://doi.org/10.20965/jrm.2022.p0361
  16. [16] U. Pinkall and K. Polthier, “Computing discrete minimal surfaces and their conjugates,” Experimental Mathematics, Vol.2, No.1, pp. 15-36, 1993.
  17. [17] G. Dziuk and J. Hutchinson, “The Discrete Plateau Problem: Algorithm and Numerics,” Mathematics of Computation, Vol.68, No.225, pp. 1-23, 1999.
  18. [18] F. Ilievski, A. D. Mazzeo, R. F. Shepherd, X. Chen, and G. M. Whitesides, “Soft robotics for chemists,” Angewandte Chemie Int. Editiion, Vol.50, Issue 8, pp. 1890-1895, 2011. https://doi.org/10.1002/anie.201006464
  19. [19] M. Botsch, L. Kobbelt, M. Pauly, P. Alliez, and B. Lévy, “Polygon Mesh Processing,” CRC Press, 2010.
  20. [20] U. Pinkall and K. Polthier, “Computing discrete minimal surfaces and their conjugates,” Experimental Mathematics, Vol.2, Issue 1, pp. 15-36, 1993. https://doi.org/10.1080/10586458.1993.10504266
  21. [21] M. Meyer, M. Desbrun, P. Schröder, and A. H. Barr, “Discrete Differential-Geometry Operators for Triangulated 2-Manifolds,” H.-C. Hege and K. Polthier (Eds.), “Visualization and Mathematics III,” pp. 35-57, Springer, 2003. https://doi.org/10.1007/978-3-662-05105-4_2
  22. [22] M. P. do Carmo, “Differential Geometry of Curves and Surfaces: Revised and Updated Second Edition,” Dover Publications, 2016.
  23. [23] S. J. Callens, N. Tümer, and A. A. Zadpoor, “Hyperbolic origami-inspired folding of triply periodic minimal surface structures,” Applied Materials Today, Vol.15, pp. 453-461, 2019. https://doi.org/10.1016/j.apmt.2019.03.007
  24. [24] N. Iwamoto, “Geometric Modeling and Estimation of Robotic Fin Shape with Bending Actuators and Passive Elements,” Sensors and Materials, Vol.35, No.9, pp. 3125-3135, 2023. https://doi.org/10.18494/SAM4387

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Mar. 04, 2025