Paper:
Control of Multiple McKibben Pneumatic Actuators Using Small Solenoid Valves and Dynamic Quantizer
Yasuhiro Sugimoto*
 , Keisuke Naniwa**
, Keisuke Naniwa**
 , Daisuke Nakanishi***
, Daisuke Nakanishi***
 , and Koichi Osuka*
, and Koichi Osuka*

*Osaka University
2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
**Hokkaido University of Science
7-Jo, 15-4-1 Maeda, Teine, Sapporo, Hokkaido 006-8585, Japan
***National Institute of Technology, Matsue College
14-4 Nishi-ikuma, Matsue, Shimane 690-8518, Japan
McKibben pneumatic actuators (MPAs) are soft actuators that exert tension by inflating a rubber tube with compressed air. Although electropneumatic regulators can control air pressure, their cost and size limit their applications. This study employs a dynamic quantizer to control an MPA using a small solenoid valve that can only open or close, as opposed to an electropneumatic regulator. A dynamic quantizer is a type of quantizer that converts continuous signals into discrete signals. Our previous study confirmed that the tension or length control of MPA can be achieved using a dynamic quantizer. As MPA exerts force only in the direction of contraction, multiple MPAs must be combined when using them as robot actuators. This study demonstrates that control using a dynamic quantizer is feasible, even when multiple MPAs are employed. We focused on a pendulum driven by two MPAs to achieve angle-tracking control using a dynamic-quantizer-based control method. The results of numerical simulations and experimental tests confirm that the angle of the pendulum can be controlled using MPAs with a dynamic quantizer.
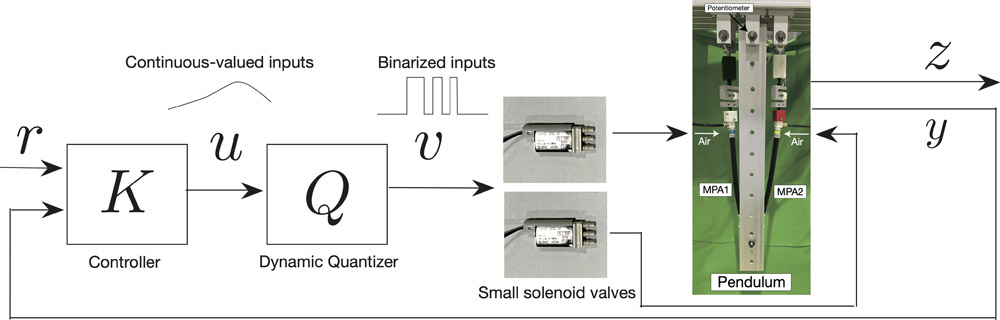
Control via small valves & dynamic quantizer
- [1] M. Agerholm and A. Lord, “The Artificial Muscle of Mckibben,” The Lancet, Vol.277, No.7178, pp. 660-661, 1961.
- [2] M. M. Gavrilović and M. R. Marić, “Positional servo-mechanism activated by artificial muscles,” Medical & Biological Engineering, Vol.7, No.1, pp. 77-82, 1969. https://doi.org/10.1007/BF02474672
- [3] A. A. M. Faudzi, G. Endo, S. Kurumaya, and K. Suzumori, “Long-Legged Hexapod Giacometti Robot Using Thin Soft McKibben Actuator,” IEEE Robotics and Automation Letters, Vol.3, No.1, pp. 100-107, 2018. https://doi.org/10.1109/LRA.2017.2734244
- [4] R. Niiyama, A. Nagakubo, and Y. Kuniyoshi, “Mowgli: A Bipedal Jumping and Landing Robot with an Artificial Musculoskeletal System,” Proc. 2007 IEEE Int. Conf. on Robotics and Automation, pp. 2546-2551, 2007. https://doi.org/10.1109/ROBOT.2007.363848
- [5] T. Takuma and K. Hosoda, “Controlling the Walking Period of a Pneumatic Muscle Walker,” The Int. J. of Robotics Research, Vol.25, No.9, pp. 861-866, 2006. https://doi.org/10.1177/0278364906069187
- [6] B. Tondu, S. Ippolito, J. Guiochet, and A. Daidie, “A Seven-degrees-of-freedom Robot-arm Driven by Pneumatic Artificial Muscles for Humanoid Robots,” The Int. J. of Robotics Research, Vol.24, No.4, pp. 257-274, 2005. https://doi.org/10.1177/0278364905052437
- [7] M. Wisse and J. von Frankenhyyzen, “Design and Construction of MIKE; A 2-D Autonomous Biped Based on Passive Dynamic Walking,” H. Kimura, K. Tsuchiya, A. Ishiguro, and H. Witte (Eds.), “Adaptive Motion of Animals and Machines,” pp. 143-154, 2006. https://doi.org/10.1007/4-431-31381-8_13
- [8] G. Andrikopoulos, G. Nikolakopoulos, and S. Manesis, “Pneumatic artificial muscles: A switching model predictive control approach,” Control Engineering Practice, Vol.21, No.12, pp. 1653-1664, 2013. https://doi.org/10.1016/j.conengprac.2013.09.003
- [9] G. Andrikopoulos, G. Nikolakopoulos, and S. Manesis, “Advanced nonlinear PID-based antagonistic control for pneumatic muscle actuators,” IEEE Trans. on Industrial Electronics, Vol.61, No.12, pp. 6926-6937, 2014. https://doi.org/10.1109/TIE.2014.2316255
- [10] Y. Cao and J. Huang, “Neural-network-based nonlinear model predictive tracking control of a pneumatic muscle actuator-driven exoskeleton,” IEEE/CAA J. of Automatica Sinica, Vol.7, No.6, pp. 1478-1488, 2020. https://doi.org/10.1109/JAS.2020.1003351
- [11] R. M. Robinson, C. S. Kothera, R. M. Sanner, and N. M. Wereley, “Nonlinear Control of Robotic Manipulators Driven by Pneumatic Artificial Muscles,” IEEE/ASME Trans. on Mechatronics, Vol.21, No.1, pp. 55-68, 2016. https://doi.org/10.1109/TMECH.2015.2483520
- [12] T. Shin, T. Ibayashi, and K. Kogiso, “Detailed Dynamic Model of Antagonistic PAM System and Its Experimental Validation: Sensorless Angle and Torque Control with UKF,” IEEE/ASME Trans. on Mechatronics, Vol.27, No.3, pp. 1715-1726, 2022. https://doi.org/10.1109/TMECH.2021.3086218
- [13] J. Cao, S. Q. Xie, and R. Das, “MIMO Sliding Mode Controller for Gait Exoskeleton Driven by Pneumatic Muscles,” IEEE Trans. on Control Systems Technology, Vol.26, No.1, pp. 274-281, 2018. https://doi.org/10.1109/TCST.2017.2654424
- [14] B. Ugurlu, P. Forni, C. Doppmann, E. Sariyildiz, and J. Morimoto, “Stable Control of Force, Position, and Stiffness for Robot Joints Powered via Pneumatic Muscles,” IEEE Trans. on Industrial Informatics, Vol.15, No.12, pp. 6270-6279, 2019. https://doi.org/10.1109/TII.2019.2916228
- [15] T. Shin and K. Kogiso, “Sensorless angle and stiffness control of antagonistic PAM actuator using reference set,” Advanced Robotics, Vol.36, No.9, pp. 423-437, 2022. https://doi.org/10.1080/01691864.2022.2046502
- [16] V. T. Jouppila, S. A. Gadsden, G. M. Bone, A. U. Ellman, and S. R. Habibi, “Sliding mode control of a pneumatic muscle actuator system with a PWM strategy,” Int. J. of Fluid Power, Vol.15, No.1, pp. 19-31, 2014. https://doi.org/10.1080/14399776.2014.893707
- [17] S. Hodgson, M. Tavakoli, M. T. Pham, and A. Leleve, “Nonlinear Discontinuous Dynamics Averaging and PWM-Based Sliding Control of Solenoid-Valve Pneumatic Actuators,” IEEE/ASME Trans. on Mechatronics, Vol.20, No.2, pp. 876-888, 2015. https://doi.org/10.1109/TMECH.2014.2326601
- [18] E. H. Skorina, M. Luo, S. Ozel, F. Chen, W. Tao, and C. D. Onal, “Feedforward augmented sliding mode motion control of antagonistic soft pneumatic actuators,” 2015 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 2544-2549, 2015. https://doi.org/10.1109/ICRA.2015.7139540
- [19] R. van Ham, B. Verrelst, F. Daerden, and D. Lefeber, “Pressure Control with On-Off Valves of Pleated Pneumatic Artificial Muscles in a Modular One-Dimensional Rotational Joint,” Int. Conf. on Humanoid Robots, 2003.
- [20] S. Jien, S. Hirai, Y. Ogawa, M. Ito, and K. Honda, “Pressure control valve for McKibben artificial muscle actuators with miniaturized unconstrained pneumatic on/off valves,” 2009 IEEE/ASME Int. Conf. on Advanced Intelligent Mechatronics, pp. 1383-1388, 2009. https://doi.org/10.1109/AIM.2009.5229882
- [21] S. Azuma and T. Sugie, “Optimal dynamic quantizers for discrete-valued input control,” Automatica, Vol.44, No.2, pp. 396-406, 2008. https://doi.org/10.1016/j.automatica.2007.06.012
- [22] Y. Minami, S. Azuma, and T. Sugie, “An optimal dynamic quantizer for feedback control with discrete-valued signal constraints,” 2007 Proc. of the IEEE Conf. on Decision and Control, pp. 2259-2264, 2007. https://doi.org/10.1109/CDC.2007.4434167
- [23] Y. Sugimoto, K. Naniwa, D. Nakanishi, and K. Osuka, “Tension Control of a McKibben Pneumatic Actuator Using a Dynamic Quantizer,” J. Robot. Mechatron., Vol.35, No.4, pp. 1038-1046, 2023. https://doi.org/10.20965/jrm.2023.p1038
- [24] Y. Sugimoto, K. Naniwa, D. Nakanishi, and K. Osuka, “Length control of a McKibben pneumatic actuator using a dynamic quantizer,” ROBOMECH J., Vol.11, Article No.8, 2024. https://doi.org/10.1186/s40648-024-00276-0
- [25] G. K. Klute, J. M. Czerniecki, and B. Hannaford, “Artificial Muscles: Actuators for Biorobotic Systems,” The Int. J. of Robotics Research, Vol.21, No.4, pp. 295-309, 2002. https://doi.org/10.1177/027836402320556331
- [26] B. Tondu and P. Lopez, “Modeling and control of McKibben artificial muscle robot actuators,” IEEE Control Systems Magazine, Vol.20, No.2, pp. 15-38, 2000. https://doi.org/10.1109/37.833638
- [27] C.-P. Chou and B. Hannaford, “Measurement and modeling of McKibben pneumatic artificial muscles,” IEEE Trans. on Robotics and Automation, Vol.12, No.1, pp. 90-102, 1996. https://doi.org/10.1109/70.481753
- [28] Y. Sugimoto, K. Naniwa, K. Osuka, and Y. Sankai, “Static and dynamic properties of McKibben pneumatic actuator for self-stability of legged-robot motion,” Advanced Robotics, Vol.27, No.6, pp. 469-480, 2013. https://doi.org/10.1080/01691864.2013.763007
- [29] D. Nakanishi, Y. Sugimoto, H. Honda, and K. Osuka, “Measurement experiments and analysis for modeling of McKibben pneumatic actuator,” J. Robot. Mechatron., Vol.28, No.6, pp. 830-836, 2016. https://doi.org/10.20965/jrm.2016.p0830
- [30] T. Goto, Y. Sugimoto, D. Nakanishi, K. Naniwa, and K. Osuka, “Analysis of Autonomous Coordination Between Actuators in the Antagonist Musculoskeletal Model,” J. Robot. Mechatron., Vol.33, No.2, pp. 410-420, 2021. https://doi.org/10.20965/jrm.2021.p0410
- [31] S. Azuma, Y. Minami, and T. Sugie, “Optimal dynamic quantizers for feedback control with discrete-level actuators: Unified solution and experimental evaluation,” J. of Dynamic Systems, Measurement and Control, Vol.133, No.2, Article No.021005, 2011. https://doi.org/10.1115/1.4002952
- [32] S. Azuma and T. Sugie, “Synthesis of optimal dynamic quantizers for discrete-valued input control,” IEEE Trans. on Automatic Control, Vol.53, No.9, pp. 2064-2075, 2008. https://doi.org/10.1109/TAC.2008.929400
- [33] K. Sawada and S. Shin, “Synthesis of decentralized dynamic quantizer within invariant set analysis framework,” IFAC Proc. Volumes, Vol.44, No.1, pp. 11284-11289, 2011. https://doi.org/10.3182/20110828-6-IT-1002.01963
- [34] S. Azuma, R. Morita, Y. Minam, and T. Sugie, “A Software Tool for Control-Oriented Dynamic Quantizer Design and Experimental Evaluation,” Trans. of the Institute of Systems, Control and Information Engineers, Vol.21, No.12, pp. 408-416, 2008. https://doi.org/10.5687/iscie.21.408
- [35] R. Morita, S. Azuma, Y. Minami, and T. Sugie, “Graphical Design Software for Dynamic Quantizers in Control Systems,” SICE J. of Control, Measurement, and System Integration, Vol.4, No.5, pp. 372-379, 2011. https://doi.org/10.9746/jcmsi.4.372
- [36] K. Tanaka, Y. Minami, and M. Ishikawa, “NQLib: A Python library for noise-shaping quantizer synthesis,” SoftwareX, Vol.27, Article No.101792, 2024. https://doi.org/10.1016/j.softx.2024.101792
- [37] T. Goto, Y. Sugimoto, D. Nakanishi, K. Naniwa, and K. Osuka, “Analysis of mode bifurcation between McKibben pneumatic actuators in the antagonist musculoskeletal model,” Nonlinear Theory and Its Applications, IEICE, Vol.13, No.4, pp. 598-614, 2022. https://doi.org/10.1587/nolta.13.598
- [38] M. Ishikawa, I. Maruta, and T. Sugie, “Compensation of Actuator Nonlinearity Using Discrete-valued Input Control Based on Feedback Modulator,” Trans. of the Society of Instrument and Control Engineers, Vol.44, No.3, pp. 288-290, 2008. https://doi.org/10.9746/ve.sicetr1965.44.288
- [39] T. Ohgi and Y. Yokokohji, “Control of Hydraulic Actuator Systems Using Feedback Modulator,” J. Robot. Mechatron., Vol.20, No.5, pp. 695-708, 2008. https://doi.org/10.20965/jrm.2008.p0695
- [40] R. Takahashi, S. Azuma, and T. Hikihara, “Power Regulation With Predictive Dynamic Quantizer in Power Packet Dispatching System,” IEEE Trans. on Industrial Electronics, Vol.63, No.12, pp. 7653-7661, 2016. https://doi.org/10.1109/TIE.2016.2591898
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.