Paper:
Multiple Power Laws and Scaling Relation in Exploratory Locomotion of the Snail Tegula nigerrima
Katsushi Kagaya*
 , Tomoyuki Nakano**
, Tomoyuki Nakano**
 , and Ryo Nakayama***
, and Ryo Nakayama***
*Kitami Institute of Technology
165 Koen-cho, Kitami, Hokkaido 090-8507, Japan
**Seto Marine Biological Laboratory, Field Science Education and Research Center, Kyoto University
459 Shirahama, Nishimuro, Wakayama 649-2211, Japan
***Fisheries Research Institute, Aomori Prefectural Industrial Technology Research Center
10 Tsukidomari, Moura, Hiranai, Higashi-Tsugaru, Aomori 039-3381, Japan
One of the goals of soft robotics is to achieve spontaneous behaviors similar to real organisms. To gain insight into these behaviors, we examined the long (16-hour) spontaneous exploratory locomotion of Tegula nigerrima, an active foraging snail from an intertidal rocky shore. Specifically, we tested the critical brain hypothesis that the nervous system is inherently near a critical state that is self-organized to drive spontaneous animal behavior. The hypothesis was originally proposed for vertebrate species, but may also be applicable to other invertebrate species. We first investigated the power spectra of snail locomotion speed (N=39). The spectra exhibited 1/fα fluctuations, which are a signature of self-organized criticality. The α value was estimated to be approximately 0.9. We further examined whether the spatial and temporal quantities showed multiple power laws and scaling relations, which are rigorous criteria for criticality. Although these criteria were satisfied over a limited range and provided limited evidence of self-organization, multiple power laws and scaling relations were satisfied overall. These results support the generalizability of the critical brain hypothesis.
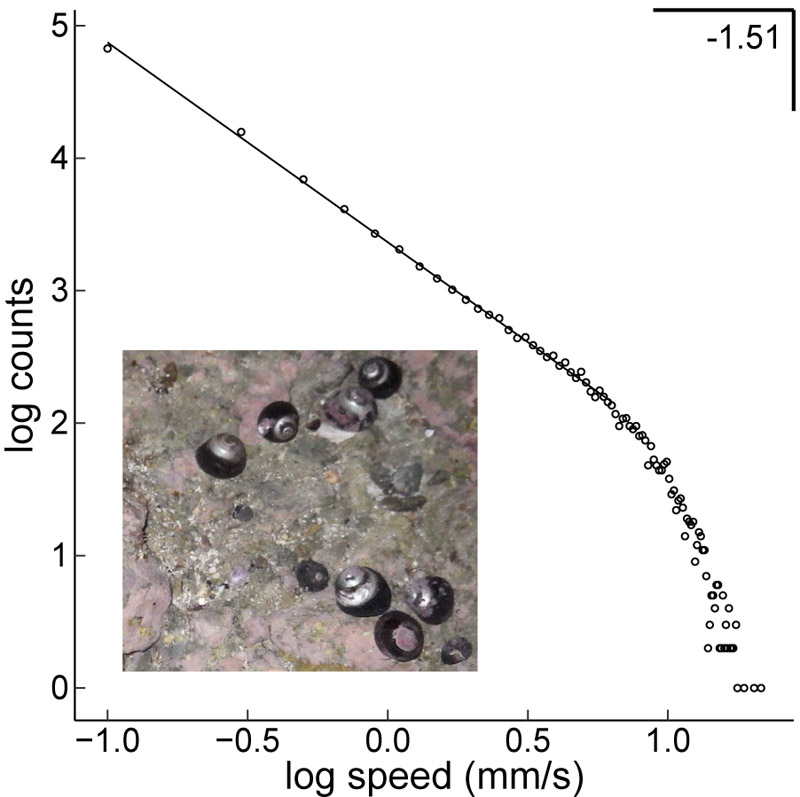
Spontaneous power-law snail exploration
- [1] R. Pfeifer, M. Lungarella, and F. Iida, “Self-organization, embodiment, and biologically inspired robotics,” Science, Vol.318, No.5853, pp. 1088-1093, 2007. https://doi.org/10.1126/science.1145803
- [2] K. Suzumori, “Overview of the Kakenhi Grant-in-Aid for Scientific Research on innovative areas: Science of soft robots,” J. Robot. Mechatron., Vol.34, No.2, pp. 195-201, 2022. https://doi.org/10.20965/jrm.2022.p0195
- [3] M. F. Shlesinger, G. M. Zaslavsky, and J. Klafter, “Strange kinetics,” Nature, Vol.363, No.6424, pp. 31-37, 1993. https://doi.org/10.1038/363031a0
- [4] D. W. Sims et al., “Scaling laws of marine predator search behaviour,” Nature, Vol.451, No.7182, pp. 1098-1102, 2008. https://doi.org/10.1038/nature06518
- [5] D. W. Sims et al., “Hierarchical random walks in trace fossils and the origin of optimal search behavior,” Proc. of the National Academy of Sciences, Vol.111, No.30, pp. 11073-11078, 2014. https://doi.org/10.1073/pnas.1405966111
- [6] A. M. Reynolds, “Current status and future directions of Lévy walk research,” Biology Open, Vol.7, No.1, Article No.bio030106, 2018. https://doi.org/10.1242/bio.030106
- [7] A. Maye, C. Hsieh, G. Sugihara, and B. Brembs, “Order in spontaneous behavior,” PLOS ONE, Vol.2, No.5, Article No.e443, 2007. https://doi.org/10.1371/journal.pone.0000443
- [8] M. S. Abe, “Functional advantages of Lévy walks emerging near a critical point,” Proc. of the National Academy of Sciences, Vol.117, No.39, pp. 24336-24344, 2020. https://doi.org/10.1073/pnas.2001548117
- [9] J. O’Byrne and K. Jerbi, “How critical is brain criticality?,” Trends in Neurosciences, Vol.45, No.11, pp. 820-837, 2022. https://doi.org/10.1016/j.tins.2022.08.007
- [10] P. Bak, C. Tang, and K. Wiesenfeld, “Self-organized criticality: An explanation of the 1/f noise,” Physical Review Letters, Vol.59, No.4, pp. 381-384, 1987. https://doi.org/10.1103/PhysRevLett.59.381
- [11] P. Bak, C. Tang, and K. Wiesenfeld, “Self-organized criticality,” Physical Review A, Vol.38, No.1, pp. 364-374, 1988. https://doi.org/10.1103/PhysRevA.38.364
- [12] P. Bak, K. Chen, and M. Creutz, “Self-organized criticality in the ‘Game of Life’,” Nature, Vol.342, No.6251, pp. 780-782, 1989. https://doi.org/10.1038/342780a0
- [13] R. Nakayama, T. Nakano, and Y. Yusa, “Seasonal utilization patterns of two snail hosts by the epizoic limpet Lottia tenuisculpta (Gastropoda: Patellogastropoda),” J. of Experimental Marine Biology and Ecology, Vols.530-531, Article No.151402, 2020. https://doi.org/10.1016/j.jembe.2020.151402
- [14] H. J. Jensen, “Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems,” Cambridge University Press, 1998.
- [15] J. P. Sethna, K. A. Dahmen, and C. R. Myers, “Crackling noise,” Nature, Vol.410, No.6825, pp. 242-250, 2001. https://doi.org/10.1038/35065675
- [16] O. Yamanaka and R. Takeuchi, “UMATracker: An intuitive image-based tracking platform,” J. of Experimental Biology, Vol.221, No.16, Article No.jeb182469, 2018. https://doi.org/10.1242/jeb.182469
- [17] J. B. Mallinson et al., “Avalanches and criticality in self-organized nanoscale networks,” Science Advances, Vol.5, No.11, Article No.eaaw8438, 2019. https://doi.org/10.1126/sciadv.aaw8438
- [18] D. W. Sims, N. E. Humphries, N. Hu, V. Medan, and J. Berni, “Optimal searching behaviour generated intrinsically by the central pattern generator for locomotion,” eLife, Vol.8, Article No.e50316, 2019. https://doi.org/10.7554/eLife.50316
- [19] J. M. Beggs and D. Plenz, “Neuronal avalanches in neocortical circuits,” J. of Neuroscience, Vol.23, No.35, pp. 11167-11177, 2003. https://doi.org/10.1523/JNEUROSCI.23-35-11167.2003
- [20] D. Plenz et al., “Self-organized criticality in the brain,” Frontiers in Physics, Vol.9, Article No.639389, 2021. https://doi.org/10.3389/fphy.2021.639389
- [21] A. Schurger, P. B. Hu, J. Pak, and A. L. Roskies, “What is the readiness potential?,” Trends in Cognitive Sciences, Vol.25, No.7, pp. 558-570, 2021. https://doi.org/10.1016/j.tics.2021.04.001
- [22] A. Schurger, J. D. Sitt, and S. Dehaene, “An accumulator model for spontaneous neural activity prior to self-initiated movement,” Proc. of the National Academy of Sciences, Vol.109, No.42, pp. E2904-E2913, 2012. https://doi.org/10.1073/pnas.1210467109
- [23] K. Kagaya and M. Takahata, “Readiness discharge for spontaneous initiation of walking in crayfish,” J. of Neuroscience, Vol.30, No.4, pp. 1348-1362, 2010. https://doi.org/10.1523/JNEUROSCI.4885-09.2010
- [24] K. Kagaya and M. Takahata, “Sequential synaptic excitation and inhibition shape readiness discharge for voluntary behavior,” Science, Vol.332, No.6027, pp. 365-368, 2011. https://doi.org/10.1126/science.1202244
- [25] K. Kagaya, T. Kubota, and K. Nakajima, “Self-organized criticality for dendritic readiness potential,” arXiv:2209.09075, 2022. https://doi.org/10.48550/arXiv.2209.09075
- [26] H. Murakami, M. S. Abe, and Y. Nishiyama, “Toward comparative collective behavior to discover fundamental mechanisms underlying behavior in human crowds and nonhuman animal groups,” J. Robot. Mechatron., Vol.35, No.4, pp. 922-930, 2023. https://doi.org/10.20965/jrm.2023.p0922
- [27] T. Ogawa and T. Nakamura, “Path tracking method for traveling-wave-type omnidirectional mobile robot (TORoIII),” J. Robot. Mechatron., Vol.24, No.2, pp. 340-346, 2012. https://doi.org/10.20965/jrm.2012.p0340
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.