Paper:
Landing Guidance Control Combining Powered Descending with Nonlinear Optimization and Vertical Descending with Model Prediction
Yusuke Nakatsuka, Satoshi Satoh
 , and Katsuhiko Yamada
, and Katsuhiko Yamada
Graduate School of Engineering, Osaka University
2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
In this study, we propose a landing guidance control method for the Moon using two control methods. The landing of a spacecraft on the Moon is divided into two phases: the powered descending phase and the vertical descending phase. The powered descending phase aims to optimize the entire trajectory to satisfy the termination constraint, instead of allowing for a relatively long control period. This phase performs feedback control using trajectory updates via nonlinear optimization. The vertical-descending phase aims to achieve accurate control over a short control period. This phase applies nonlinear model predictive control for fast optimization on finite time intervals. First, the landing of a spacecraft on the Moon is modeled as a two-body problem of the Moon and spacecraft, and equations of motion are derived. Subsequently, we formulated an optimization problem for each phase and developed the proposed landing guidance method by combining the two control methods. Furthermore, numerical simulations based on the derived equations of motion were performed to confirm the effectiveness of the proposed method and to compare its performance with another optimization method, the successive convexification (SCvx) algorithm.
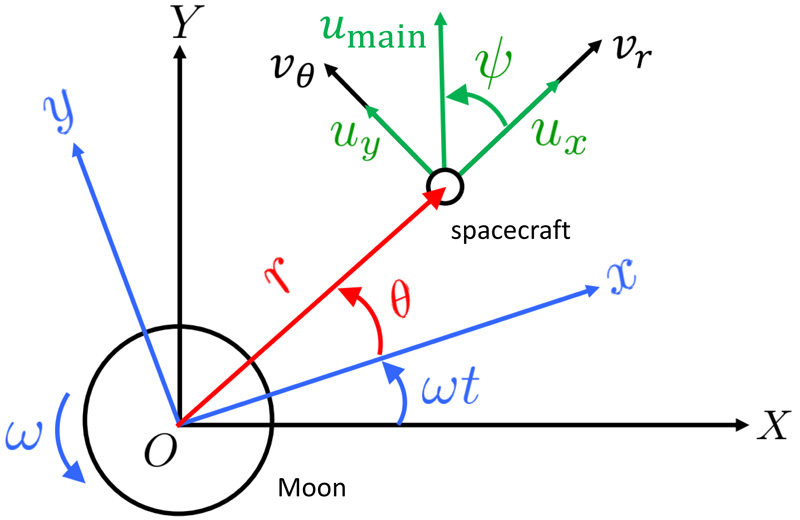
Coordinate setting
- [1] S. Sakai and K. Kushiki, “Overview on a small lunar lander project SLIM,” Proc. 64th Space Sciences and Technology Conf., 2020.
- [2] H. Shimoji, H. Saito, Y. Shimizu, Y. Shibasaki, K. Shuto, K. Sawayama, A. Chiba, Y. Munemoto, T. Matsuda, T. Niwa, K. Nakamura, Y. Tanaka, J. Kono, D. Watabe, Y. Mukumoto, Y. Hamafuku, Y. Oikawa, J. Otsubo, A. Sugihara, F. Komagata, M. Oba, Y. Aoki, S. Sakai, K. Kushiki, S. Sawai, and S. Fukuda, “System design and development test of SLIM,” Proc. 64th Space Sciences and Technology Conf., 2020.
- [3] G. Fujii, K. Michigami, H. Tani, K. Kawatsu, Y. Daimon, K. Kushiki, S. Sawai, and S. Sakai, “The SLIM propulsion system combustion test results and reflection on system design,” Proc. 64th Space Sciences and Technology Conf., 2020.
- [4] M. Kato, S. Sasaki, Y. Takizawa, and the Kaguya project team, “The Kaguya mission overview,” Space Science Reviews, Vol.154, pp. 3-19, 2010. https://doi.org/10.1007/s11214-010-9678-3
- [5] S. Ueda, T. Ito, and S. Sakai, “Resilience enhancement of lunar landing trajectory control using reinforcement learning,” Trans. the Society of Instrument and Control Engineers, Vol.58, No.3, pp. 194-201, 2022. https://doi.org/10.9746/sicetr.58.194
- [6] A. Scorsoglio, A. D’Ambrosio, L. Ghilardi, B. Gaudet, F. Curti, and R. Furfaro, “Image-based deep reinforcement meta-learning for autonomous lunar landing,” J. Spacecraft and Rockets, Vol.59, No.1, pp. 153-165, 2022. https://doi.org/10.2514/1.A35072
- [7] L. Sun, G. Sun, and J. Jiang, “Adaptive guidance and control of uncertain lunar landers in terminal landing phases,” Mechanical Systems and Signal Processing, Vol.142, Article No.106763, 2020. https://doi.org/10.1016/j.ymssp.2020.106763
- [8] I. M. Mehedi and T. Kubota, “A trajectory generation scheme for precise and safe lunar landing,” J. Space Engineering, Vol.4, No.1, pp. 1-13, 2011. https://doi.org/10.1299/spacee.4.1
- [9] S. Ueda, T. Ito, and S. Sakai, “A study on guidance technique for precise lunnar landing,” Proc. 31st Int. Symp. Space Technology and Science, 2017.
- [10] X. L. Liu, G. R. Duan, and K. L. Teo, “Optimal soft landing control for moon lander,” Automatica, Vol.44, No.4, pp. 1097-1103, 2008. https://doi.org/10.1016/j.automatica.2007.08.021
- [11] T. Otsuka, “Practical Applications of Control by Real-Time Optimization,” Corona Publishing Co., Ltd., 2015.
- [12] T. Higuchi, S. Ueno, and Y. Kimura, “Optimal trajectory of powered descending phase with coasting for smart lander for investigating moon,” Proc. 60th Space Sciences and Technology Conf., 2016.
- [13] Y. Mao, M. Szmuk, and B. Açıkmeşe, “Successive convexification of non-convex optimal control problems and its convergence properties,” IEEE 55th Conf. on Decision and Control, 2016. https://doi.org/10.1109/CDC.2016.7798816
- [14] M. Szmuk and B. Açıkmeşe, “Successive convexification for 6-dof mars rocket powered landing with free-final-time,” AIAA Guidance, Navigation, and Control Conf., 2018. https://doi.org/10.2514/6.2018-0617
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.