Paper:
Design of a Hierarchical-Type Control System Based on Smart MBD Approach and its Application to Hydraulic Excavator
Shin Wakitani*
 , Mikiya Sako*, Toru Yamamoto*
, Mikiya Sako*, Toru Yamamoto*
 , Yohei Ohno**, Hiromu Kishi**, Natsuki Yumoto**, and Kazushige Koiwai**
, Yohei Ohno**, Hiromu Kishi**, Natsuki Yumoto**, and Kazushige Koiwai**
*Hiroshima University
1-4-1 Kagamiyama, Higsahi-hiroshima, Hiroshima 739-8527, Japan
**KOBELCO Construction Machinery Co., Ltd.
2-2-1 Itsukaichikou, Saeki-ku, Hiroshima 731-5161, Japan
Model-based development (MBD), which utilizes system models to design complex products, has received increasing attention. However, an advanced control system design scheme is required to accurately control the developed products under harsh conditions for practical usage. This paper proposes a control system that integrates a data-driven compensator (DDC) with a model-based control (MBC) system design. The proposed method considers a hierarchical control structure comprising an upstream control system based on the MBC design approach and a downstream control system that includes a plant control loop with a DDC. The proposed system can always maintain the desired performance by driving the MBC based on an ideal model because the downstream control system, DDC, maintains the characteristics of the ideal model even if the plant properties change owing to changes in operational and/or environmental conditions. In this study, the design scheme for unifying models and data in the MBD process is called smart MBD (S-MBD), and the proposed control system design scheme is based on the S-MBD approach. The effectiveness of the proposed hierarchical control system is verified by applying it to a hydraulic excavator.
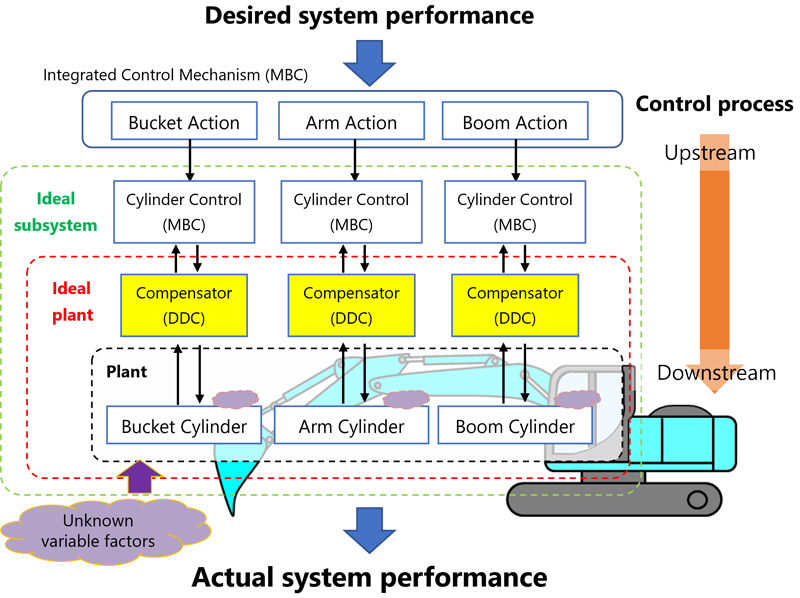
Hierarchical-type control system based on S-MBD approach
- [1] J. M. Thate, L. E. Kendrick, and S. Nadarajah, “Caterpillar Automatic Code Generation,” SAE 2004 World Congress & Exhibition, Article No.2004-01-0894, 2004. https://doi.org/10.4271/2004-01-0894
- [2] A. Ohata and K. R. Butts, “Improving Model-based Design for Automotive Control Systems Development,” IFAC Proc. Volumes, Vol.41, Issue 2, pp. 1062-1065, 2008. https://doi.org/10.3182/20080706-5-KR-1001.00182
- [3] K. Beckers, I. Côté, T. Frese, D. Hatebur, and M. Heisel, “A structured and systematic model-based development method for automotive systems, considering the OEM/supplier interface,” Reliability Engineering & System Safety, Vol.158, pp. 172-184, 2017. https://doi.org/10.1016/j.ress.2016.08.018
- [4] M. Sako, S. Wakitani, M. Kozui, T. Yamamoto, K. Yamashita, K. Koiwai, and Y. Yamazaki, “Design and Practice of a Model-Based Development Education in Hydraulic Systems,” J. Robot. Mechatron., Vol.32, No.3, pp. 662-671, 2020. https://doi.org/10.20965/jrm.2020.p0662
- [5] K. Tateyama, “Achievement and Future Prospects of ICT Construction in Japan,” J. Robot. Mechatron., Vol.28, No.2, pp. 123-128, 2016. https://doi.org/10.20965/jrm.2016.p0123
- [6] T. Shintani, Y. Saito, Y. Kiritani, S. Ozawa, and K. Obayashi, “Applying Model-based Development to Performance Development of Hydraulic Excavators Using 1DCAE,” Komatsu Technical Report, Vol.67, No.174, pp. 2-10, 2021.
- [7] D. Piga, S. Formentin, and A. Bemporad, “Direct Data-Driven Control of Constrained Systems,” IEEE Trans. on Control Systems Technology, Vol.26, No.4, pp. 1422-1429, 2018. https://doi.org/10.1109/TCST.2017.2702118
- [8] M. C. Campi, A. Lecchini, and S. M. Savaresi, “Virtual reference feedback tuning (VRFT): A new direct approach to the design of feedback controllers,” Proc. of the 39th IEEE Conf. on Decision and Control (Cat. No.00CH37187), Vol.1, pp. 623-629, 2000. https://doi.org/10.1109/CDC.2000.912835
- [9] M. P. Polverini, S. Formentin, L. Merzagora, and P. Rocco, “Mixed Data-Driven and Model-Based Robot Implicit Force Control: A Hierarchical Approach,” IEEE Trans. on Control Systems Technology, Vol.28, No.4, pp. 1258-1271, 2020. https://doi.org/10.1109/TCST.2019.2908899
- [10] O. Kaneko, “Data-Driven Controller Tuning: FRIT Approach,” IFAC Proc. Volumes, Vol.46, Issue 11, pp. 326-336, 2013. https://doi.org/10.3182/20130703-3-FR-4038.00122
- [11] M. Sekine, S. Tsuruhara, and K. Ito, “MPC for Artificial Muscles Using FRIT based Optimized Pseudo Linearization Model,” IFAC-PapersOnLine, Vol.56, Issue 2, pp. 7264-7269, 2023. https://doi.org/10.1016/j.ifacol.2023.10.336
- [12] O. Kaneko and T. Nakamura, “Data-driven prediction of 2DOF control systems with updated feedforward controller,” 2017 56th Annual Conf. of the Society of Instrument and Control Engineers of Japan (SICE), pp. 259-262, 2017. https://doi.org/10.23919/SICE.2017.8105636
- [13] S. Ishihara, R. Narikawa, and T. Ohtsuka, “Automated Loading Operation for Mass-Production Hydraulic Excavators by Nonlinear Model Predictive Control,” IFAC-PapersOnLine, Vol.56, Issue 2, pp. 5793-5798, 2023. https://doi.org/10.1016/j.ifacol.2023.10.554
- [14] S. Wakitani, M. Sako, T. Yamamoto, Y. Ohno, N. Yumoto, K. Koiwai, and K. Yamashita, “Study on Control System Design based on Smart Model Based Development Approach and its Application for a Hydraulic Excavator,” 2022 IEEE Int. Symp. on Advanced Control of Industrial Processes (AdCONIP), pp. 297-298, 2022. https://doi.org/10.1109/AdCONIP55568.2022.9894201
- [15] T. Kitamori, “A Method of Control System Design Based upon Partial Knowledge about Controlled Processes,” Trans. of the Society of Instrument and Control Engineers, Vol.15, No.4, pp. 549-555, 1979 (in Japanese). https://doi.org/10.9746/sicetr1965.15.549
- [16] S. Kawai and N. Hori, “Interpretation of Kitamori’s Partial-Model-Matching Method in a Descriptor-Form Expression,” 2020 IEEE Conf. on Control Technology and Applications (CCTA), pp. 928-932, 2020. https://doi.org/10.1109/CCTA41146.2020.9206292
- [17] H. Okajima, H. Umei, N. Matsunaga, and T. Asai, “A Design Method of Compensator to Minimize Model Error,” SICE J. of Control, Measurement, and System Integration, Vol.6, Issue 4, pp. 267-275, 2013. https://doi.org/10.9746/jcmsi.6.267
- [18] H. Endo, K. Sekiguchi, and K. Nonaka, “Online Adjustment Method of Model Error Compensator,” Trans. of the Society of Instrument and Control Engineers, Vol.55, No.3, pp. 156-163, 2019 (in Japanese).
- [19] Y. Wakasa, K. Tanaka, and Y. Nishimura, “Online Controller Tuning via FRIT and Recursive Least-Squares,” IFAC Proc. Volumes, Vol.45, Issue 3, pp. 76-80, 2012. https://doi.org/10.3182/20120328-3-IT-3014.00013
- [20] A. Patete, K. Furuta, and M. Tomizuka, “Self-tuning control based on generalized minimum variance criterion for auto-regressive models,” Automatica, Vol.44, Issue 8, pp. 1970-1975, 2008. https://doi.org/10.1016/j.automatica.2007.11.008
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.