Paper:
Motion Planning for Throwing Manipulation Using Bayesian Optimization
Tasuku Yamawaki
 , Chihaya Yamamoto, and Masahito Yashima
, Chihaya Yamamoto, and Masahito Yashima

National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
Throwing manipulation utilizes virtual driving forces, such as gravity, centrifugal force, and Coriolis force, to extend the workspace and increase the degrees of freedom available for manipulation. However, it is highly sensitive to various uncertainties such as wind disturbance and measurement noise, thereby deteriorating the throwing performance. This study proposes a motion planning method that uses Bayesian optimization to obtain an optimal arm trajectory for throwing manipulation through repeated trials. Bayesian optimization can explicitly account for stochastic uncertainties and obtain an optimal solution with a small number of trials. The key contributions of the proposed method are the explicit modeling of stochastic uncertainties using a Gaussian distribution and the ability to reduce the number of retraining attempts. The efficacy of the proposed motion planning method was validated through extensive experiments. Specifically, in environments with randomly changing wind directions and wind speeds, experiments demonstrated that the proposed method generated throwing motions that were more robust against wind disturbances than conventional methods based on iterative learning methods. Furthermore, even when the throwing target point is changed, the experiments demonstrate that the proposed learning method can learn with fewer trials than the conventional method by utilizing past observation data.
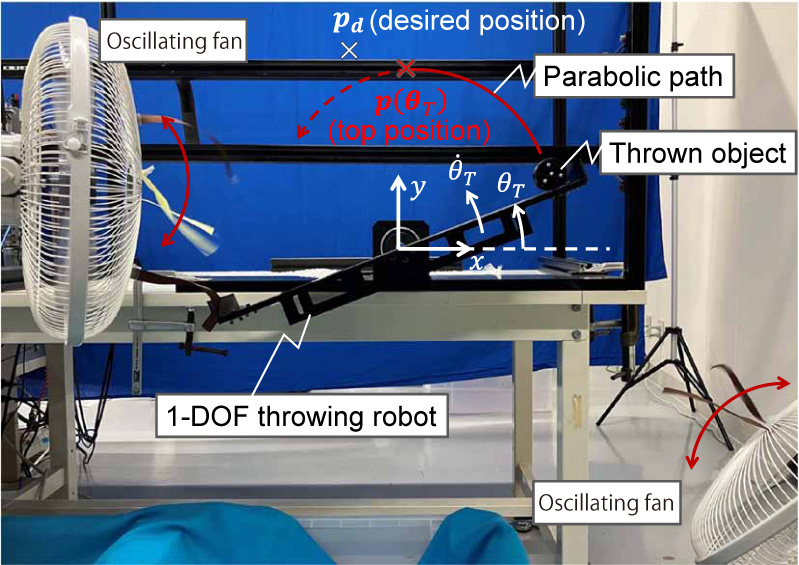
Throwing objects under wind disturbance
- [1] J. Z. Woodruff and K. M. Lynch, “Planning and control for dynamic, nonprehensile, and hybrid manipulation tasks,” 2017 IEEE Int. Conf. on Robotics and Automation, pp. 4066-4073, 2017. https://doi.org/10.1109/ICRA.2017.7989467
- [2] N. C. Dafle, A. Rodriguez, R. Paolini, B. Tang, S. S. Srinivasa, M. Erdmann, M. T. Mason, I. Lundberg, H. Staab, and T. Fuhlbrigge, “Extrinsic dexterity: In-hand manipulation with external forces,” 2014 IEEE Int. Conf. on Robotics and Automation, pp. 1578-1585, 2014. https://doi.org/10.1109/ICRA.2014.6907062
- [3] K. M. Lynch and M. T. Mason, “Dynamic nonprehensile manipulation: Controllability, planning, and experiments,” The Int. J. of Robotics Research, Vol.18, No.1, pp. 64-92, 1999. https://doi.org/10.1177/027836499901800105
- [4] H. Frank and R. Koblinger, “Throwing and capturing of workpieces by robots – New transport services for the internet-of-things in production systems,” Proc. of the 10th Int. Conf. on Informatics in Control, Automation and Robotics, pp. 434-438, 2013. https://doi.org/10.5220/0004584004340438
- [5] A. Pekarovskiy and M. Buss, “Optimal control goal manifolds for planar nonprehensile throwing,” 2013 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 4518-4524, 2013. https://doi.org/10.1109/IROS.2013.6697006
- [6] W. Mori, J. Ueda, and T. Ogasawara, “1-DOF dynamic pitching robot that independently controls velocity, angular velocity, and direction of a ball: Contact models and motion planning,” 2009 IEEE Int. Conf. on Robotics and Automation, pp. 1655-1661, 2009. https://doi.org/10.1109/ROBOT.2009.5152525
- [7] A. Sintov and A. Shapiro, “A stochastic dynamic motion planning algorithm for object-throwing,” 2015 IEEE Int. Conf. on Robotics and Automation, pp. 2475-2480, 2015. https://doi.org/10.1109/ICRA.2015.7139530
- [8] O. Taylor and A. Rodriguez, “Optimal shape and motion planning for dynamic planar manipulation,” Autonomous Robots, Vol.43, No.2, pp. 327-344, 2019. https://doi.org/10.1007/s10514-018-9773-y
- [9] A. Zeng, S. Song, J. Lee, A. Rodriguez, and T. Funkhouser, “Tossingbot: Learning to throw arbitrary objects with residual physics,” IEEE Trans. on Robotics, Vol.36, No.4, pp. 1307-1319, 2020. https://doi.org/10.1109/TRO.2020.2988642
- [10] J. Kober, E. Oztop, and J. Peters, “Reinforcement learning to adjust robot movements to new situations,” Int. Joint Conf. on Artificial Intelligence, Best Paper Track, pp. 2650-2655, 2011.
- [11] A. Ghadirzadeh, A. Maki, D. Kragic, and M. Björkman, “Deep predictive policy training using reinforcement learning,” 2017 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 2351-2358, 2017. https://doi.org/10.1109/IROS.2017.8206046
- [12] E. W. Aboaf, C. G. Atkeson, and D. J. Reinkensmeyer, “Task-level robot learning,” Proc. of the 1988 IEEE Int. Conf. on Robotics and Automation, pp. 1309-1310, 1988. https://doi.org/10.1109/ROBOT.1988.12245
- [13] M. Yashima, H. Miyashita, and T. Yamawaki, “Throwing manipulation by one joint robot,” Trans. of the Japan Society of Mechanical Engineers, Series C, Vol.75, No.759, pp. 3005-3010, 2009 (in Japanese). https://doi.org/10.1299/kikaic.75.3005
- [14] H. Miyashita, T. Yamawaki, and M. Yashima, “Parts assembly and sorting by throwing manipulation: Planning and control,” J. of System Design and Dynamics, Vol.5, No.1, pp. 139-154, 2011. https://doi.org/10.1299/jsdd.5.139
- [15] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams, and N. de Freitas, “Taking the human out of the loop: A review of Bayesian optimization,” Proc. of the IEEE, Vol.104, No.1, pp. 148-175, 2016. https://doi.org/10.1109/JPROC.2015.2494218
- [16] J. Snoek, H. Larochelle, and R. P. Adams, “Practical Bayesian optimization of machine learning algorithms,” F. Pereira, C. J. Burges, L. Bottou, and K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems, Vol.25, Curran Associates, 2012.
- [17] R. Calandra, A. Seyfarth, J. Peters, and M. P. Deisenroth, “An experimental comparison of Bayesian optimization for bipedal locomotion,” 2014 IEEE Int. Conf. on Robotics and Automation, pp. 1951-1958, 2014. https://doi.org/10.1109/ICRA.2014.6907117
- [18] D. Lizotte, T. Wang, M. Bowling, and D. Schuurmans, “Automatic gait optimization with Gaussian process regression,” Proc. of the 20th Int. Joint Conf. on Artificial Intelligence, pp. 944-949, 2007.
- [19] M. Tesch, J. Schneider, and H. Choset, “Using response surfaces and expected improvement to optimize snake robot gait parameters,” 2011 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 1069-1074, 2011. https://doi.org/10.1109/IROS.2011.6095076
- [20] C. E. Rasmussen and C. K. I. Williams, “Gaussian Processes for Machine Learning,” The MIT Press, 2005. https://doi.org/10.7551/mitpress/3206.001.0001
- [21] D. R. Jones, M. Schonlau, and W. J. Welch, “Efficient global optimization of expensive black-box functions,” J. of Global Optimization, Vol.13, No.4, pp. 455-492, 1998. https://doi.org/10.1023/A:1008306431147
- [22] N. Srinivas, A. Krause, S. M. Kakade, and M. W. Seeger, “Information-theoretic regret bounds for Gaussian process optimization in the bandit setting,” IEEE Trans. on Information Theory, Vol.58, No.5, pp. 3250-3265, 2012. https://doi.org/10.1109/TIT.2011.2182033
- [23] H. J. Kushner, “A new method of locating the maximum point of an arbitrary multipeak curve in the presence of noise,” J. of Basic Engineering, Vol.86, No.1, pp. 97-106, 1964. https://doi.org/10.1115/1.3653121
- [24] V. Picheny, T. Wagner, and D. Ginsbourger, “A benchmark of kriging-based infill criteria for noisy optimization,” Structural and Multidisciplinary Optimization, Vol.48, pp. 607-626, 2013. https://doi.org/10.1007/s00158-013-0919-4
- [25] G. Y. Chin, “Two-dimensional measures of accuracy in navigational systems,” U. S. Department of Transportation, Transportation Systems Center, Tech. Rep. DOT-TSC-RSPA-87-1, 1987.
- [26] B. Chen, R. M. Castro, and A. Krause, “Joint optimization and variable selection of high-dimensional Gaussian processes,” Int. Conf. on Machine Learning, pp. 1379-1386, 2012.
- [27] C. J. Paciorek and M. J. Schervish, “Spatial modeling using a new class of nonstationary covariance functions,” Environmetrics, Vol.17, No.5, pp. 483-506, 2006. https://doi.org/10.1002/env.785
- [28] D. Higdon, J. Swall, and J. Kern, “Non-stationary spatial modeling,” Bayesian Statistics 6, pp. 761-768, Clarendon Press, 1999. https://doi.org/10.1093/oso/9780198504856.003.0036
- [29] M. Feurer, J. Springenberg, and F. Hutter, “Initializing Bayesian hyperparameter optimization via meta-learning,” Proc. of the AAAI Conf. on Artificial Intelligence, Vol.29, No.1, pp. 1128-1135, 2015. https://doi.org/10.1609/aaai.v29i1.9354
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.