Paper:
Adaptive Kinematic Control of Underwater Cable-Driven Parallel Robot
Katutoshi Kodama*, Akihiro Morinaga*, and Ikuo Yamamoto**

*Graduate School of Engineering, Nagasaki University
1-14 Bunkyo-machi, Nagasaki-city, Nagasaki 852-8521, Japan
**Organization for Marine Science and Technology, Nagasaki University
1-14 Bunkyo-machi, Nagasaki-city, Nagasaki 852-8521, Japan
We previously proposed on the underwater cable-driven parallel robot (UCDPR), a system comprising multiple surface robots, and designed a modeling and trajectory tracking control method for it. However, the conventional trajectory tracking control of the UCDPR using the kinematic controller faced several issues. These included challenges in control gain tuning due to model uncertainty and a decline in trajectory tracking performance caused by changes in system characteristics due to environmental factors like current velocity. In response, this study focuses on the development of an adaptive kinematic controller. The aim is to mitigate the effects of uncertainties and other factors while ensuring effective trajectory tracking. This is achieved by incorporating an adaptive modification term into the conventional kinematic controller, which can be tuned adaptively in real-time. To validate the effectiveness of the adaptive kinematic controller, we conducted numerical simulations using a planar 2-DOF UCDPR.
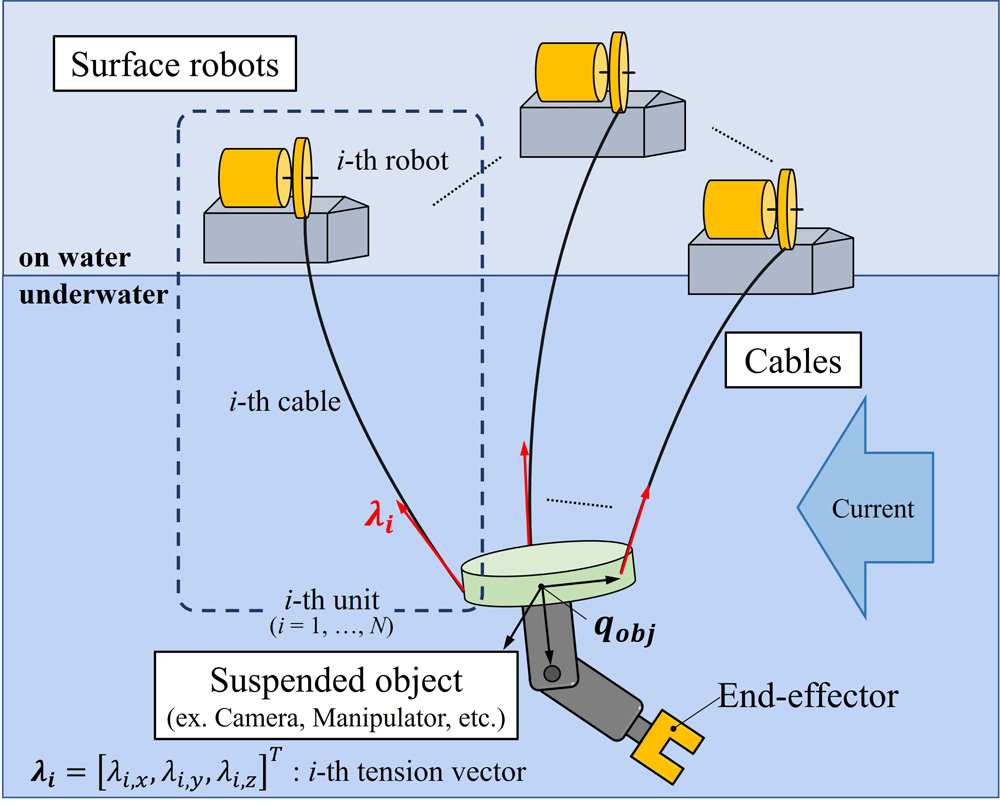
Concept image of UCDPR
- [1] H. Kino and S. Kawamura, “Mechanism and Control of Parallel-Wire Driven System,” J. Robot. Mechatron, Vol.27, No.6, pp. 599-607, 2015. https://doi.org/10.20965/jrm.2015.p0599
- [2] A. Pott, “Cable-Driven Parallel Robots: Theory and Application,” 1st ed., Chapter 2, Springer, 2018. https://doi.org/10.1007/978-3-319-76138-1
- [3] T. Rasheed, “Collaborative Mobile Cable-Driven Parallel Robots,” École centrale de Nantes, Ph.D. thesis, 2019.
- [4] N. Pedemonte, T. Rasheed, D. Marquez-Gamez, P. Long, É. Hocquard, F. Babin, C. Fouché, G. Caverot, A. Girin, and S. Caro, “FASTKIT: A Mobile Cable-Driven Parallel Robot for Logistics,” Advances in Robotics Research: From Lab to Market, Springer, pp. 141-163, 2020. https://doi.org/10.1007/978-3-030-22327-4_8
- [5] T. Rasheed, P. Long, P. D. Marquez-Gamez, and S. Caro, “Path Planning of a Mobile Cable-Driven Parallel Robot in a Constrained Environment,” Proc. of the 4th Int. Conf. on Cable-Driven Parallel Robots (Mechanisms and Machine Science), Vol.74, pp. 257-268, 2019. https://doi.org/10.1007/978-3-030-20751-9_22
- [6] N. Michael, J. Fink, and V. Kumar, “Cooperative manipulation and transportation with aerial robots,” Autonomous Robots, Vol.30, pp. 73-86, 2011. https://doi.org/10.1007/s10514-010-9205-0
- [7] G. A. Cardona, D. Tellez-Castro, and E. Mojica-Nava, “Cooperative Transportation of a Cable-Suspended Load by Multiple Quadrotors,” IFAC-PapersOnLine, Vol.52, No.20, pp. 145-150, 2019. https://doi.org/10.1016/j.ifacol.2019.12.149
- [8] F. Takemura and S. Sagara, “Proposal of a sectional wire drive under water robot,” Proc. of Robomech2008, 2A1-A05, 2008. https://doi.org/10.1299/jsmermd.2008._2A1-A05_1
- [9] K. Kodama, A. Morinaga, and I. Yamamoto, “Development of Parallel Wire Driven System Composed of Multiple On-water Omni-Directional Mobile Robots,” Proc. of SICE SI2021, pp. 1488-1493, 2021 (in Japanese).
- [10] K. Kodama, A. Morinaga, and I. Yamamoto, “Mathematic Modeling of Underwater Cable-Driven Parallel System Considering the Dynamics of Cables,” Proc. of Robomech2022, 2A1-B07, 2022 (in Japanese). https://doi.org/10.1299/jsmermd.2022.2A1-B07
- [11] K. Kodama, A. Morinaga, and I. Yamamoto, “Control for Underwater Cable-Driven Parallel Robot by Redundant Degrees of Freedom,” Proc. of SICE SI2022, pp. 929-932, 2022 (in Japanese).
- [12] K. Kodama, A. Morinaga, and I. Yamamoto, “Mathematic Modeling and Control of Underwater Cable-Driven Parallel Robot,” J. Jpn. Soc. Nav. Archit. Ocean Eng., Vol.36, pp. 53-67, 2022 (in Japanese). https://doi.org/10.2534/jjasnaoe.36.53
- [13] Y. Miyazato, “Adaptive Control,” 1st ed., Chapters 1 and 4, Corona Publishing Co., Ltd., 2018 (in Japanese).
- [14] N. Mizuno, “Basic Adaptive Control – Theory, Implementation, Application,” 1st ed., Chapter 1, Corona Publishing Co., Ltd., 2020 (in Japanese).
- [15] H. Kumamoto, I. Sakamoto, and H. Kawabata, “Self-Tuning PID Controller for First and Second Order Lag Systems,” Trans. of SICE, Vol.33, No.5, pp. 344-541, 1997 (in Japanese). https://doi.org/10.9746/sicetr1965.33.344
- [16] H. Kino, T. Yoshitake, R. Wada, K. Tahara, and K. Tsuda, “3-DOF Planar Parallel-Wire Driven Robot with an Active Balancer and Its Model-Based Adaptive Control,” Advanced Robotics, Vol.32, No.14, pp. 766-777, 2018. https://doi.org/10.1080/01691864.2018.1493397
- [17] H. A. Godbole, R. J. Caverly, and J. R. Forbes, “Dynamic Modeling and Adaptive Control of a Single Degree-of-Freedom Flexible Cable-Driven Parallel Robot,” J. Dyn. Sys., Meas., Control., Vol.141, No.10, Article No.101002, 2019. https://doi.org/10.1115/1.4043427
- [18] Y. Taira, “Robust Control for Underwater Robot Manipulators with a Time-Varying Feedback Gain,” J. of National Fisheries University, Vol.58, No.3, pp. 199-205, 2010 (in Japanese).
- [19] J. W. Kamman and R. L. Huston, “Multibody Dynamics Modeling of Variable Length Cable Systems,” Multibody System Dynamics, Vol.5, pp. 211-221, 2001. https://doi.org/10.1023/A:1011489801339
- [20] S. Kata, “A Program for Two-Dimensional Dynamic Analysis of Forces on Mooring Line by Use of Lumped Mass Method,” Papers of Ship Research Institute, Vol.21, No.5, pp. 247-249, 1984 (in Japanese).
- [21] J. Baumgarte, “Stabilization of constraints and integrals of motion in dynamical systems,” Computer Methods in Applied Mechanics and Engineering, Vol.1, No.1, pp. 1-16, 1972. https://doi.org/10.1016/0045-7825(72)90018-7
- [22] A. Keymasi Khalaji, “Modeling and Control of Uncertain Multibody Wheeled Robots,” Multibody System Dynamics, Vol.46, pp. 257-279, 2019. https://doi.org/10.1007/s11044-019-09673-5
- [23] M. Tarokh and D. D. Zuck, “Robust Adaptive Kinematic Control of Redundant Robots,” NASA Technical Report, 1992.
- [24] M. Yamamoto, “Stability of Ordinary Differential Equations,” 1st ed., Chapter 1, Jikkyo-Syuppan Co., Ltd., 1979 (in Japanese).
- [25] K. Hirai, “Nonlinear Control,” 3rd ed., Chapter 4, Corona Publishing Co., Ltd., 2010 (in Japanese).
- [26] K. Kodama, A. Morinaga, and I. Yamamoto, “Development and Simulation of Operational Scenarios for Underwater Cable-Drive Parallel Robot,” Sens. Mater., Vol.35, No.2, pp. 377-389, 2023 (in press).
- [27] M. Yamamoto, N. Yanai, and A. Mohri, “Inverse Dynamics and Control of a Crane-Type Manipulator with Multi-Degrees of Freedom,” J. of the Robotics Society of Japan, Vol.17, No.7, pp. 1037-1043, 1999 (in Japanese). https://doi.org/10.7210/jrsj.17.1037
- [28] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams, and N. Freitas, “Taking the Human Out of the Loop: A Review of Bayesian Optimization,” Proc. of the IEEE, Vol.104, No.1, pp. 148-175, 2016. https://doi.org/10.1109/JPROC.2015.2494218
- [29] S. Masuda and H. Ohmori, “Adaptive Control for Freshmen, Controlling while Modeling,” J. of SICE, Vol.42, No.4, pp. 297-303, 2003 (in Japanese). https://doi.org/10.11499/sicejl1962.42.297
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.