Paper:
Tension Control of a McKibben Pneumatic Actuator Using a Dynamic Quantizer
Yasuhiro Sugimoto*
 , Keisuke Naniwa*
, Keisuke Naniwa*
 , Daisuke Nakanishi**
, Daisuke Nakanishi**
 , and Koichi Osuka*
, and Koichi Osuka*

*Osaka University
2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
**National Institute of Technology, Matsue College
14-4 Nishi-ikuma, Matsue, Shimane 690-8518, Japan
A McKibben-type pneumatic actuator (MPA) is a soft actuator that generates tension by inflating a rubber tube with compressed air. Electropneumatic regulators are typically employed to regulate air pressure in MPAs. However, they are normally large in size and expensive, which are significant obstacles to the autonomous decentralized control of many MPAs in achieving various robot motions. In this study, the exerted tension of the MPA was controlled using a small solenoid valve that could be opened and closed instead of an electropneumatic regulator. To achieve this tension control, we proposed the use of a dynamic quantizer that converts continuous pressure values into discrete pressure values and controls the solenoid valve based on the discretized pressure values. The proposed method was applied to feedforward and feedback control of the exerted MPA tension under isometric conditions. Experiments on an actual device with a small solenoid valve demonstrated the effectiveness of the proposed method based on a dynamic quantizer.
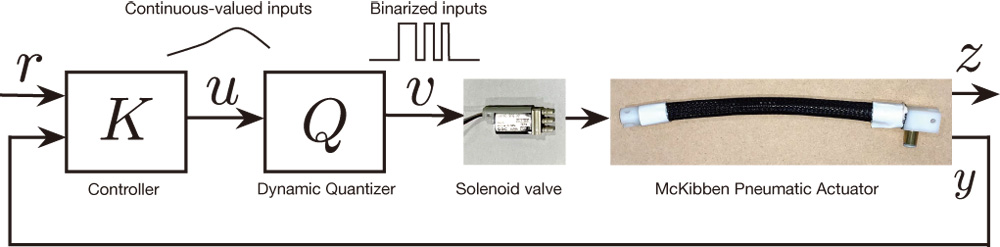
Tension control with a dynamic quantizer
- [1] M. Agerholm and A. Lord, “The “Artificial Muscle” of McKibben,” The Lancet, Vol.277, No.7178, pp. 660-661, 1961. https://doi.org/10.1016/S0140-6736(61)91676-2
- [2] M. M. Gavrilović and M. R. Marić, “Positional servo-mechanism activated by artificial muscles,” Medical & Biological Engineering & Computing, Vol.7, No.1, pp. 77-82, 1969. https://doi.org/10.1007/BF02474672
- [3] A. A. M. Faudzi, G. Endo, S. Kurumaya, and K. Suzumori, “Long-Legged Hexapod Giacometti Robot Using Thin Soft McKibben Actuator,” IEEE Robotics and Automation Letters, Vol.3, No.1, pp. 100-107, 2018. https://doi.org/10.1109/LRA.2017.2734244
- [4] R. Niiyama, A. Nagakubo, and Y. Kuniyoshi, “Mowgli: A Bipedal Jumping and Landing Robot with an Artificial Musculoskeletal System,” Proc. 2007 IEEE Int. Conf. on Robotics and Automation, pp. 2546-2551, 2007. https://doi.org/10.1109/ROBOT.2007.363848
- [5] T. Takuma and K. Hosoda, “Controlling the Walking Period of a Pneumatic Muscle Walker,” The Int. J. of Robotics Research, Vol.25, No.9, pp. 861-866, 2006. https://doi.org/10.1177/0278364906069187
- [6] B. Tondu, S. Ippolito, J. Guiochet, and A. Daidie, “A Seven-Degrees-of-Freedom Robot-Arm Driven by Pneumatic Artificial Muscles for Humanoid Robots,” The Int. J. of Robotics Research, Vol.24, No.4, pp. 257-274, 2005. https://doi.org/10.1177/0278364905052437
- [7] M. Wisse and J. von Frankenhyyzen, “Design and Construction of MIKE; A 2-D Autonomous Biped Based on Passive Dynamic Walking,” Adaptive Motion of Animals and Machines, pp. 143-154, 2003. https://doi.org/10.1007/4-431-31381-8_13
- [8] G. Andrikopoulos, G. Nikolakopoulos, and S. Manesis, “Pneumatic artificial muscles: A switching Model Predictive Control approach,” Control Engineering Practice, Vol.21, No.12, pp. 1653-1664, 2013. https://doi.org/10.1016/j.conengprac.2013.09.003
- [9] G. Andrikopoulos, G. Nikolakopoulos, and S. Manesis, “Advanced nonlinear PID-based antagonistic control for pneumatic muscle actuators,” IEEE Trans. on Industrial Electronics, Vol.61, No.12, pp. 6926-6937, 2014. https://doi.org/10.1109/TIE.2014.2316255
- [10] Y. Cao and J. Huang, “Neural-network-based nonlinear model predictive tracking control of a pneumatic muscle actuator-driven exoskeleton,” IEEE/CAA J. of Automatica Sinica, Vol.7, No.6, pp. 1478-1488, 2020. https://doi.org/10.1109/JAS.2020.1003351
- [11] R. M. Robinson, C. S. Kothera, R. M. Sanner, and N. M. Wereley, “Nonlinear Control of Robotic Manipulators Driven by Pneumatic Artificial Muscles,” IEEE/ASME Trans. on Mechatronics, Vol.21, No.1, pp. 55-68, 2016. https://doi.org/10.1109/TMECH.2015.2483520
- [12] T. Shin, T. Ibayashi, and K. Kogiso, “Detailed Dynamic Model of Antagonistic PAM System and its Experimental Validation: Sensorless Angle and Torque Control With UKF,” IEEE/ASME Trans. on Mechatronics, Vol.27, No.3, pp. 1715-1726, 2022. https://doi.org/10.1109/TMECH.2021.3086218
- [13] V. T. Jouppila, S. A. Gadsden, G. M. Bone, A. U. Ellman, and S. R. Habibi, “Sliding mode control of a pneumatic muscle actuator system with a PWM strategy,” Int. J. of Fluid Power, Vol.15, No.1, pp. 19-31, 2014. https://doi.org/10.1080/14399776.2014.893707
- [14] R. V. Ham, B. Verrelst, F. Daerden, and D. Lefeber, “Pressure Control with On-Off Valves of Pleated Pneumatic Artificial Muscles in a Modular One-Dimensional Rotational Joint,” Int. Conf. on Humanoid Robots, 2003.
- [15] S. Jien, S. Hirai, Y. Ogawa, M. Ito, and K. Honda, “Pressure Control Valve for McKibben Artificial Muscle Actuators with Miniaturized Unconstrained Pneumatic on/off Valves,” 2009 IEEE/ASME Int. Conf. on Advanced Intelligent Mechatronics, pp. 1383-1388, 2009. https://doi.org/10.1109/AIM.2009.5229882
- [16] S. Azuma and T. Sugie, “Optimal dynamic quantizers for discrete-valued input control,” Automatica, Vol.44, No.2, pp. 396-406, 2008. https://doi.org/10.1016/j.automatica.2007.06.012
- [17] Y. Minami, S. Azuma, and T. Sugie, “An optimal dynamic quantizer for feedback control with discrete-valued signal constraints,” Proc. of the IEEE Conf. on Decision and Control, pp. 2259-2264, 2007. https://doi.org/10.1109/CDC.2007.4434167
- [18] C.-P. Chou and B. Hannaford, “Measurement and modeling of McKibben pneumatic artificial muscles,” IEEE Trans. on Robotics and Automation, Vol.12, No.1, pp. 90-102, 1996. https://doi.org/10.1109/70.481753
- [19] T. Goto, Y. Sugimoto, D. Nakanishi, K. Naniwa, and K. Osuka, “Analysis of autonomous coordination between actuators in the antagonist musculoskeletal model,” J. Robot. Mechatron., Vol.33, No.2, pp. 410-420, 2021. https://doi.org/10.20965/jrm.2021.p0410
- [20] G. K. Klute, J. M. Czerniecki, and B. Hannaford, “Artificial Muscles: Actuators for Biorobotic Systems,” The Int. J. of Robotics Research, Vol.21, No.4, pp. 295-309, 2002. https://doi.org/10.1177/027836402320556331
- [21] D. Nakanishi, Y. Sugimoto, H. Honda, and K. Osuka, “Experiments and analysis for modeling of McKibben pneumatic actuator,” J. of Robotics and Mechatronics, Vol.28, No.6, pp. 830-836, 2016. https://doi.org/10.20965/jrm.2016.p0830
- [22] Y. Sugimoto, K. Naniwa, K. Osuka, and Y. Sankai, “Static and dynamic properties of McKibben pneumatic actuator for self-stability of legged-robot motion,” Advanced Robotics, Vol.27, No.6, pp. 469-480, 2013. https://doi.org/10.1080/01691864.2013.763007
- [23] B. Tondu and P. Lopez, “Modeling and control of McKibben artificial muscle robot actuators,” IEEE Control Systems Magazine, Vol.20, No.2, pp. 15-38, 2000. https://doi.org/10.1109/37.833638
- [24] S. Azuma, Y. Minami, and T. Sugie, “Optimal dynamic quantizers for feedback control with discrete-level actuators: Unified solution and experimental evaluation,” J. of Dynamic Systems, Measurement and Control, Vol.133, No.2, pp. 1-10, 2011. https://doi.org/10.1115/1.4002952
- [25] S. Azuma and T. Sugie, “Synthesis of optimal dynamic quantizers for discrete-valued input control,” IEEE Trans. on Automatic Control, Vol.53, No.9, pp. 2064-2075, 2008. https://doi.org/10.1109/TAC.2008.929400
- [26] K. Sawada and S. Shin, “Synthesis of decentralized dynamic quantizer within invariant set analysis framework,” IFAC Proc. Volumes, Vol.44, No.1, pp. 11284-11289, 2011. https://doi.org/10.3182/20110828-6-IT-1002.01963
- [27] S. Azuma, R. Morita, Y. Minami, and T. Sugie, “A Software Tool for Control-Oriented Dynamic Quantizer Design and Experimental Evaluation,” Trans. of the Institute of Systems, Control and Information Engineers, Vol.21, No.12, pp. 408-416, 2008. https://doi.org/10.5687/iscie.21.408
- [28] R. Morita, S. Azuma, Y. Minami, and T. Sugie, “Graphical Design Software for Dynamic Quantizers in Control Systems,” SICE J. of Control, Measurement, and System Integration, Vol.4, No.5, pp. 372-379, 2011. https://doi.org/10.9746/jcmsi.4.372
- [29] M. Pipan and N. Herakovič, “Volume Flow Characterization of PWM-Controlled Fast-Switching Pneumatic Valves,” J. of Mechanical Engineering, Vol.62, No.9, pp. 543-550, 2016. https://doi.org/10.5545/sv-jme.2016.3531
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.