Paper:
Bi-Connectivity Control for Multi-Robot Network Considering Line-of-Sight Communication
Toru Murayama
 and Aoi Iwasaki
and Aoi Iwasaki
National Institute of Technology, Wakayama College
77 Noshima, Nada, Gobo, Wakayama 644-0023, Japan
This study proposes a bi-connectivity control algorithm for a multi-robot system consisting of a robot that communicates through line-of-sight communication. Optical observation and communication require a line of sight to a subject, and a robot in a multi-robot system sometimes impedes the line of sight between other robots. The motion of individual robots may violate the connectivity of the communication network. A distributed control strategy for bi-connectivity was constructed by modifying a previous method that does not consider line-of-sight restrictions. The results of the numerical simulation and experiments with actual robots are reported to emphasize the validity of the proposed control method.
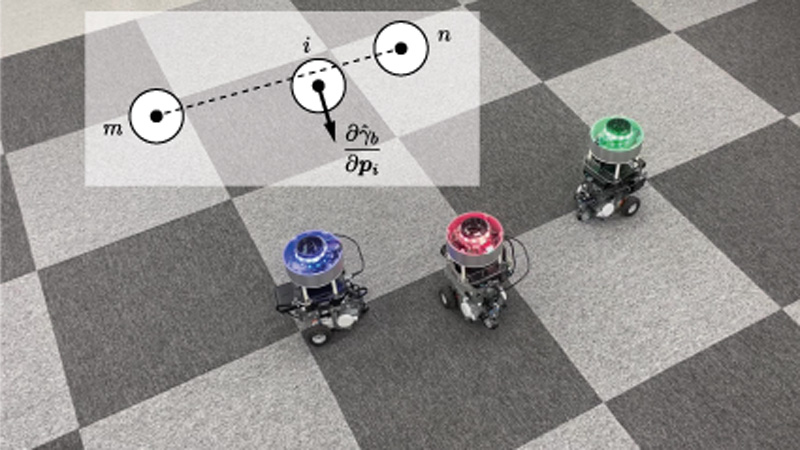
Restore bi-connectivity of line-of-sight network
- [1] J. Cortés and M. Egerstedt, “Coordinated control of multi-robot systems: A survey,” SICE J. of Control, Measurement, and System Integration, Vol.10, No.6, pp. 495-503, 2017. https://doi.org/10.9746/jcmsi.10.495
- [2] M. Dorigo, G. Theraulaz, and V. Trianni, “Reflections on the future of swarm robotics,” Science Robotics, Vol.5, No.49, Article No.eabe4385, 2020. https://doi.org/10.1126/scirobotics.abe4385
- [3] A. Shirsat, K. Elamvazhuthi, and S. Berman, “Multi-robot target search using probabilistic consensus on discrete Markov chains,” 2020 IEEE Int. Symp. on Safety, Security, and Rescue Robotics (SSRR), pp. 108-115, 2020. https://doi.org/10.1109/SSRR50563.2020.9292589
- [4] H. A. Poonawala, A. C. Satici, H. Eckert, and M. W. Spong, “Collision-free formation control with decentralized connectivity preservation for nonholonomic-wheeled mobile robots,” IEEE Trans. on Control of Network Systems, Vol.2, No.2, pp. 122-130, 2015. https://doi.org/10.1109/TCNS.2014.2378876
- [5] Y. Kantaros, M. Thanou, and A. Tzes, “Distributed coverage control for concave areas by a heterogeneous Robot-Swarm with visibility sensing constraints,” Automatica, Vol.53, pp. 195-207, 2015. https://doi.org/10.1016/j.automatica.2014.12.034
- [6] X. Sun, S. Wang, and D. Ding, “Optimal coverage control of multi-agent systems in constrained environments with line-of-sight connectivity preservation,” 2020 39th Chinese Control Conf. (CCC), pp. 4616-4621, 2020. https://doi.org/10.23919/CCC50068.2020.9188844
- [7] L. Sabattini, C. Secchi, N. Chopra, and A. Gasparri, “Distributed control of multirobot systems with global connectivity maintenance,” IEEE Trans. on Robotics, Vol.29, No.5, pp. 1326-1332, 2013. https://doi.org/10.1109/TRO.2013.2267971
- [8] L. Siligardi et al., “Robust area coverage with connectivity maintenance,” 2019 Int. Conf. on Robotics and Automation (ICRA), pp. 2202-2208, 2019. https://doi.org/10.1109/ICRA.2019.8793555
- [9] P. R. Giordano, A. Franchi, C. Secchi, and H. H. Bülthoff, “A passivity-based decentralized strategy for generalized connectivity maintenance,” The Int. J. of Robotics Research, Vol.32, No.3, pp. 299-323, 2013. https://doi.org/10.1177/0278364912469671
- [10] Y. Ikemoto, K. Nishimura, Y. Mizutama, T. Sasaki, and M. Jindai, “Network connectivity control of mobile robots by fast position estimations and Laplacian kernel,” J. Robot. Mechatron., Vol.32, No.2, pp. 422-436, 2020. https://doi.org/10.20965/jrm.2020.p0422
- [11] M. Zavlanos and G. J. Pappas, “Distributed connectivity control of mobile networks,” IEEE Trans. on Robotics, Vol.24, No.6, pp. 1416-1428, 2008. https://doi.org/10.1109/TRO.2008.2006233
- [12] D. V. Dimarogonas and K. J. Kyriakopoulos, “Connectedness preserving distributed swarm aggregation for multiple kinematic robots,” IEEE Trans. on Robotics, Vol.24, No.5, pp. 1213-1223, 2008. https://doi.org/10.1109/TRO.2008.2002313
- [13] A. Gasparri, A. Leccese, L. Sabattini, and G. Ulivi, “Collective control objective and connectivity preservation for multi-robot systems with bounded input,” 2014 American Control Conf., pp. 813-818, 2014. https://doi.org/10.1109/ACC.2014.6859070
- [14] W. Huang, Y. Wang, and X. Yi, “Deep Q-learning to preserve connectivity in multi-robot systems,” Proc. of the 9th Int. Conf. on Signal Processing Systems (ICSPS 2017), pp. 45-50, 2017. https://doi.org/10.1145/3163080.3163113
- [15] J. Scherer and B. Rinner, “Multi-robot persistent surveillance with connectivity constraints,” IEEE Access, Vol.8, pp. 15093-15109, 2020. https://doi.org/10.1109/ACCESS.2020.2967650
- [16] Y. Dong, “Rendezvous with connectivity preservation for multi-robot systems with an unknown leader,” Int. J. of Control, Vol.91, No.2, pp. 470-479, 2018. https://doi.org/10.1080/00207179.2017.1285055
- [17] M. Zareh, L. Sabattini, and C. Secchi, “Enforcing biconnectivity in multi-robot systems,” 2016 IEEE 55th Conf. on Decision and Control (CDC), pp. 1800-1805, 2016. https://doi.org/10.1109/CDC.2016.7798526
- [18] W. Luo and K. Sycara, “Minimum k-connectivity maintenance for robust multi-robot systems,” 2019 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 7370-7377, 2019. https://doi.org/10.1109/IROS40897.2019.8968058
- [19] T. Murayama, “Distributed control for bi-connectivity of multi-robot network,” SICE J. of Control, Measurement, and System Integration, 2022. https://doi.org/10.1080/18824889.2022.2157194
- [20] P. Yang et al., “Decentralized estimation and control of graph connectivity in mobile sensor networks,” 2008 American Control Conf., pp. 2678-2683, 2008. https://doi.org/10.1109/ACC.2008.4586897
- [21] T. Hiasa and T. Murayama, “Development of experimental multi-robot system for network connectivity controls,” J. Robot. Mechatron., Vol.34, No.5, pp. 1185-1191, 2022. https://doi.org/10.20965/jrm.2022.p1185
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.