Paper:
Cooperative Passing Based on Chaos Theory for Multiple Robot Swarms
Kohei Yamagishi and Tsuyoshi Suzuki
Tokyo Denki University
5 Senju Asahi-cho, Adachi-ku, Tokyo 120-8551, Japan
Swarm robotics can cooperatively perform large, multiple tasks by controlling a swarm composed of many robots. Currently, approaches for operating multiple robot swarms are being studied for further evolution of this system. This study addresses a multiple movement task in which robot swarms move collectively in the same environment. In this task, the movement paths of robot swarms must pass each other in a cooperative manner when they intersect. The robots in this system behave under autonomous distributed control, thus must consider a passing behavior suitable for their own situation. This study proposes a turning behavior based on the chaos theory to ensure that a robot swarm avoids other approaching robot swarms. Each robot swarm applying the proposed method passes other swarms while autonomously deciding its turning direction and continuing its own collective movement task. In addition, the decision making based on the chaos theory predicts future values according to the current value. Therefore, it is expected to be useful for task scheduling. The performance of multiple robots passing each other is evaluated with the proposed method using numerical simulations. This performance shows that the robot swarms can avoid each other without collision using the closest inter-robot distance as the evaluation metric. Finally, robot swarms with varying shapes and scales complete their own movements in an environment where these movement paths intersect at a single point.
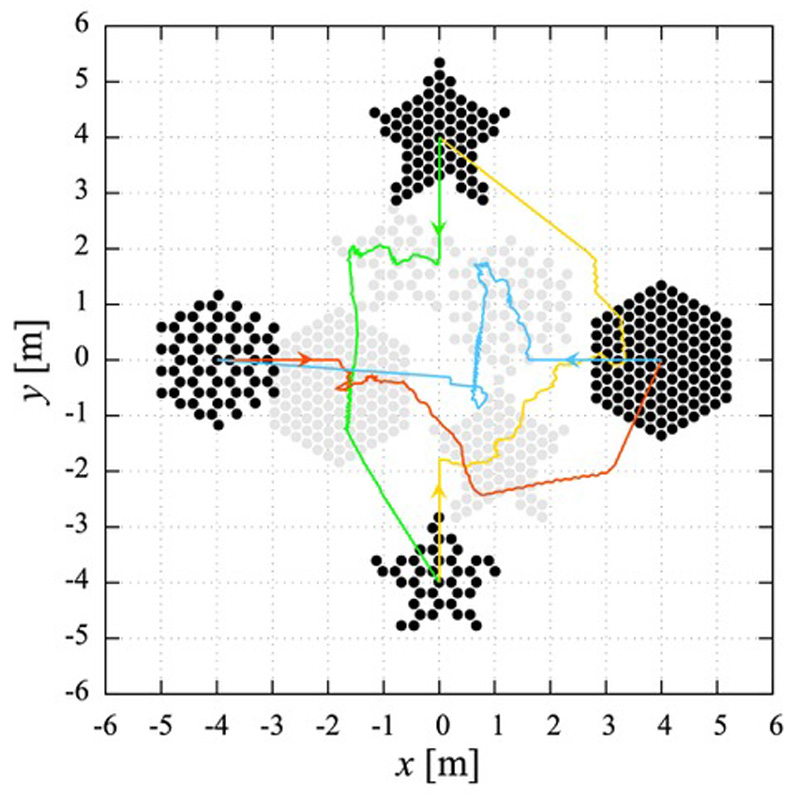
Position swapping among robot swarms
- [1] M. Dorigo, G. Theraulaz, and V. Trianni, “Swarm Robotics: Past, Present, and Future [Point of View],” Proc. of the IEEE, Vol.109, No.7, pp. 1152-1165, 2021. https://doi.org/10.1109/JPROC.2021.3072740
- [2] P. G. F. Dias, M. C. Silva, G. P. R. Filho, P. A. Vargas, L. P. Cota, and G. Pessin, “Swarm Robotics: A Perspective on the Latest Reviewed Concepts and Applications,” Sensors, Vol.21, No.6, Article No.2062, 2021. https://doi.org/10.3390/s21062062
- [3] D. Albiero, A. P. Garcia, C. K. Umezu, and R. L. de Paulo, “Swarm Robots in Mechanized Agricultural Operations: A Review About Challenges for Research,” Computers and Electronics in Agriculture, Vol.193, Aticle No.106608, 2022. https://doi.org/10.1016/j.compag.2021.106608
- [4] M. Jurt, E. Milner, M. Sooriyabandara, and S. Hauert, “Collective Transport of Arbitrarily Shaped Objects Using Robot Swarms,” Artificial Life and Robotics, Vol.27, No.2, pp. 365-372, 2022. https://doi.org/10.1007/s10015-022-00730-5
- [5] E. Camci, D. R. Kripalani, L. Ma, E. Kayacan, and M. A. Khanesar, “An Aerial Robot for Rice Farm Quality Inspection with Type-2 Fuzzy Neural Networks Tuned by Particle Swarm Optimization-Sliding Mode Control Hybrid Algorithm,” Swarm and Evolutionary Computation, Vol.41, pp. 1-8, 2018. https://doi.org/10.1016/j.swevo.2017.10.003
- [6] F. Xue, T. Dong, S. You, Y. Liu, H. Tang, L. Chen, X. Yang, and J. Li, “A Hybrid Many-Objective Competitive Swarm Optimization Algorithm for Large-Scale Multirobot Task Allocation Problem,” Int. J. of Machine Learning and Cybernetics, Vol.12, No.4, pp. 943-957, 2021. https://doi.org/10.1007/s13042-020-01213-4
- [7] H. Zhao, H. Liu, Y.-W. Leung, and X. Chu, “Self-Adaptive Collective Motion of Swarm Robots,” IEEE Trans. on Automation Science and Engineering, Vol.15, No.4, pp. 1533-1545, 2018. https://doi.org/10.1109/TASE.2018.2840828
- [8] S. Hoshino, R. Takisawa, and Y. Kodama, “Swarm Robotic Systems Based on Collective Behavior of Chloroplasts,” J. Robot. Mechatron., Vol.29, No.3, pp. 602-612, 2017. https://doi.org/10.20965/jrm.2017.p0602
- [9] K. Inoue, J. Ota, and T. Arai, “Iterative Transportation by Multiple Mobile Robots Considering Unknown Obstacles,” J. Robot. Mechatron., Vol.21, No.1, pp. 44-56, 2009. https://doi.org/10.20965/jrm.2009.p0044
- [10] Y. Kobayashi, Y. Sato, and M. Gouko, “Division of Iterative-Transportation Based on Local Observation by Multiple Mobile Robots,” J. Adv. Comput. Intell. Intell. Inform., Vol.16, No.3, pp. 462-468, 2012. https://doi.org/10.20965/jaciii.2012.p0462
- [11] M. Chandarana, D. Hughes, M. Lewis, K. Sycara, and S. Scherer, “Planning and Monitoring Multi-Job Type Swarm Search and Service Missions,” J. of Intelligent & Robotic Systems, Vol.101, No.3, Article No.44, 2021. https://doi.org/10.1007/s10846-020-01272-3
- [12] J. Wen, L. He, and F. Zhu, “Swarm Robotics Control and Communications: Imminent Challenges for Next Generation Smart Logistics,” IEEE Communications Magazine, Vol.56, No.7, pp. 102-107, 2018. https://doi.org/10.1109/MCOM.2018.1700544
- [13] Y. Yaguchi and K. Tamagawa, “A Waypoint Navigation Method with Collision Avoidance Using an Artificial Potential Method on Random Priority,” Artificial Life and Robotics, Vol.25, No.2, pp. 278-285, 2020. https://doi.org/10.1007/s10015-020-00583-w
- [14] B. Zhang and H. P. Gavin, “Natural Deadlock Resolution for Multi-Agent Multi-Swarm Navigation,” 2021 60th IEEE Conf. on Decision and Control (CDC), pp. 5958-5963, 2021. https://doi.org/10.1109/CDC45484.2021.9683102
- [15] L. Luo, X. Wang, J. Ma, and Y.-S. Ong, “GrpAvoid: Multigroup Collision-Avoidance Control and Optimization for UAV Swarm,” IEEE Trans. on Cybernetics, Vol.53, No.3, pp. 1776-1789, 2023. https://doi.org/10.1109/TCYB.2021.3132044
- [16] W. Luo, W. Sun, and A. Kapoor, “Multi-Robot Collision Avoidance Under Uncertainty with Probabilistic Safety Barrier Certificates,” Proc. of the 34th Int. Conf. on Neural Information Processing Systems (NIPS’20), pp. 372-383, 2020.
- [17] H. Zhu and J. Alonso-Mora, “B-UAVC: Buffered Uncertainty-Aware Voronoi Cells for Probabilistic Multi-Robot Collision Avoidance,” 2019 Int. Symp. on Multi-Robot and Multi-Agent Systems (MRS), pp. 162-168, 2019. https://doi.org/10.1109/MRS.2019.8901092
- [18] K. Yamagishi and T. Suzuki, “Regular Tessellation-Based Collective Movement for a Robot Swarm with Varying Densities, Scales, and Shapes,” Advances in Science, Technology and Engineering Systems J., Vol.7, No.6, pp. 31-38, 2022. https://doi.org/10.25046/aj070604
- [19] R. M. May, “Simple Mathematical Models with Very Complicated Dynamics,” Nature, Vol.261, No.5560, pp. 459-467, 1976. https://doi.org/10.1038/261459a0
- [20] J. von Neumann, “Various Techniques Used in Connection with Random Digits,” U.S. Department of Commerce, National Bureau of Standards, “Monte Carlo Method (Allpied Mathematics Series 12),” pp. 36-38, 1951.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.