Paper:
Musculoskeletal Model Capable of Reproducing Lumbar Extension Motion Strategy Based on the Equilibrium Point Hypothesis
Masahiro Sato*, Michihiro Yoshida*
 , Takashi Kusaka**
, Takashi Kusaka**
 , Yusuke Suzuki*, and Takayuki Tanaka**,†
, Yusuke Suzuki*, and Takayuki Tanaka**,†

*Graduate School of Information Science and Technology, Hokkaido University
Kita 14, Nishi 9, Kita-ku, Sapporo, Hokkaido 060-0814, Japan
**Faculty of Information Science and Technology, Hokkaido University
Kita 14, Nishi 9, Kita-ku, Sapporo, Hokkaido 060-0814, Japan
†Corresponding author
We considered the change in joint stiffness as a motion strategy in human lumbar extension movement. We developed a musculoskeletal model that can reproduce this motion strategy and attempted to clarify the individual characteristics and differences in motion strategy. This model reproduces changes in lumbar joint stiffness during movement by appropriately adjusting parameters such that they represent the motion strategy. Using this model, we identified parameters in lumbar extension exercises for six participants with differences in lumbar joint stiffness and examined changes in lumbar joint stiffness and motion strategies. The results showed that participants with similar changes in joint stiffness had commonalities in their motion strategies.
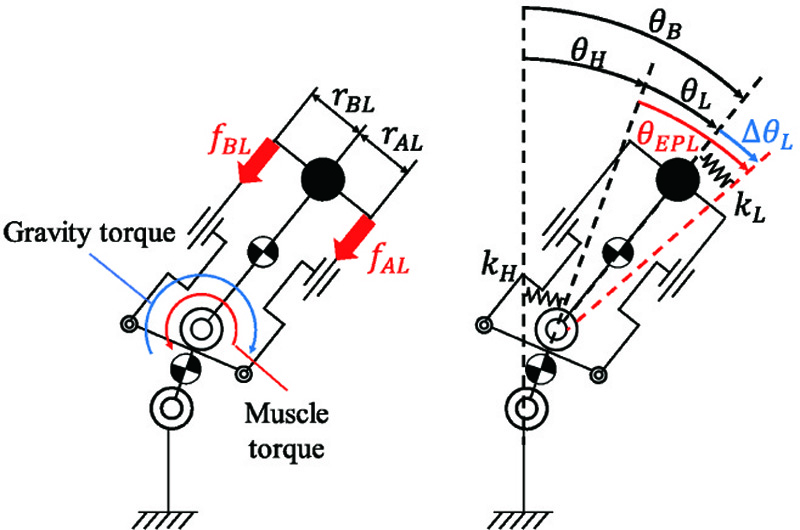
Link model joint angle
- [1] F. A. Mussa-Ivaldi, N. Hogan, and E. Bizzi, “Neural, mechanical, and geometric factors subserving arm posture in humans,” J. of Neuroscience, Vol.5, No.10, pp. 2732-2743, 1985.
- [2] T. Tsuji, K. Goto, K. Ito, and M. Nagamachi, “Estimation of Human Hand Impedance During Maintenance of Posture,” Trans. of the Society of Instrument and Control Engineers, Vol.30, No.3, pp. 319-328, 1994.
- [3] H. Gomi and M. Kawato, “Human arm stiffness and equilibrium-point trajectory during multi-joint movement,” Biological Cybernetics, Vol.76, No.3, pp. 163-171, 1997.
- [4] M. Yoshida, T. Tanaka, Y. Tsuchiya, and T. Kusaka, “Reducing lumbar load with active corset,” J. Robot. Mechatron., Vol.30, No.5, pp. 740-751, 2018.
- [5] M. Yoshida, T. Tanaka, Y. Kaneko, and Y. Tsuchiya, “Effect of Dynamic Tightening Force by Active Corset on Joint Stiffness and Lumbar Assisting,” Trans. of the Society of Instrument and Control Engineers, Vol.55, No.11, pp. 683-691, 2019.
- [6] A. G. Feldman, “Once more on the equilibrium-point hypothesis (lambda model) for motor control,” J. of Motor Behavior, Vol.18, No.1, pp. 17-54, 1986.
- [7] P. B. C. Matthews, “The dependence of tension upon extension in the stretch reflex of the soleus muscle of the decerebrate cat,” J. of Physiology, Vol.147, No.3, pp. 521-546, 1959.
- [8] R. Shadmehe and M. A. Arbib, “A mathematical analysis of the force-stiffness characteristics of muscles in control of a single joint system,” Biological Cybernetics, Vol.66, No.6, pp. 463-477, 1992.
- [9] J. A. Hoffer and S. Andreassen, “Regulation of soleus muscle stiffness in premammillary cats: Intrinsic and reflex components,” J. of Neurophysiology, Vol.45, No.2, pp. 267-285, 1981.
- [10] E. Bizzi, N. Accornero, W. Chapple, and N. Hogan, “Posture control and trajectory formation during arm movement,” J. of Neuroscience, Vol.4, No.11, pp. 2738-2744, 1984.
- [11] N. Hogan, “An organizing principle for a class of voluntary movements,” J. of Neuroscience, Vol.4, No.11, pp. 2745-2754, 1984.
- [12] T. Flash, “The control of hand equilibrium trajectories in multi-joint arm movements,” Biological Cybernetics, Vol.57, No.4, pp. 257-274, 1987.
- [13] M. Sato, T. Tanaka, M. Yoshida, and Y. Suzuki, “Lumbar mechanical model capable of reproducing joint stiffness changes during lumbar extension motion,” 2023 IEEE/SICE Int. Symp. on System Integration (SII), 2023. https://doi.org/10.1109/SII55687.2023.10039166
- [14] M. Ae, H.-P. Tang, and T. Yokoi, “Estimation of Inertia Properties of the Body Segments in Japanese Athletes,” Biomechanisms, Vol.11, pp. 23-33, 1992.
- [15] R. D. Crowninshield and R. A. Brand, “A physiologically based criterion of muscle force prediction in locomotion,” J. of Biomechanics, Vol.14, No.11, pp. 793-801, 1981.
- [16] D. Kogawa, H. Hirai, and H. Okamoto, “Classification of the runner’s preferences in running shoes based on equilibrium-point-based muscle synergies,” Proc. of the 13th Conf. of the Int. Sports Engineering Association, Vol.49, No.1, Article No.85, 2020.
- [17] K. Noro, H. Hirai, H. Okamoto et al., “Asymmetric Inter-Limb Coordination in the Legs of 10–11-Year-Old Boys during Overground Sprinting,” J. of the Robotics Society of Japan, Vol.40, No.3, pp. 259-262, 2022.
- [18] J.-S. Oh, “Effects of pelvic belt on hip extensor muscle EMG activity during prone hip extension in females with chronic low back pain,” J. of Physical Therapy Science, Vol.26, No.7, pp. 1023-1024, 2014.
- [19] L. Sawle, J. Freeman, J. Marsden, and M. J. Matthews, “Exploring the effect of pelvic belt configurations upon athletic lumbopelvic pain,” Prosthetics and Orthotics Int., Vol.37, No.2, pp. 124-131, 2013.
- [20] O. Soisson, J. Lube, A. Germano et al., “Pelvic belt effects on pelvic morphometry, muscle activity and body balance in patients with sacroiliac joint dysfunction,” PLoS ONE, Vol.10, No.3, Article No.e0116739, 2015.
- [21] J. Bertuit, C. E. V. Lint, M. Rooze, and V. Feipel, “Pregnancy and pelvic girdle pain: Analysis of pelvic belt on pain,” J. of Clinical Nursing, Vol.27, Nos.1-2, pp. e129-e137, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.