Paper:
Continuous-Time Receding-Horizon Estimation via Primal-Dual Dynamics on Vehicle Path-Following Control
Kaito Sato and Kenji Sawada

The University of Electro-Communications
1-5-1 Chofugaoka, Chofu, Tokyo 182-8585, Japan
In vehicle control, state estimation is essential even as the sensor accuracy improves with technological development. One of the vehicle estimation methods is receding-horizon estimation (RHE), which uses a past series of the measured state and input of the plant, and determines the estimated states based on linear or quadratic programming. It is known that RHE can estimate the vehicular state to which the extended Kalman filter cannot be applied owing to modeling errors. This study proposes a new computational form of the RHE based on primal-dual dynamics. The proposed form is expressed by a dynamic system; therefore, we can consider the computational stability based on the dynamic system theory. In this study, we propose a continuous-time representation of the RHE algorithm and redundant filters to improve the convergence performance of the estimation and demonstrate its effectiveness through a vehicle path-following control problem.
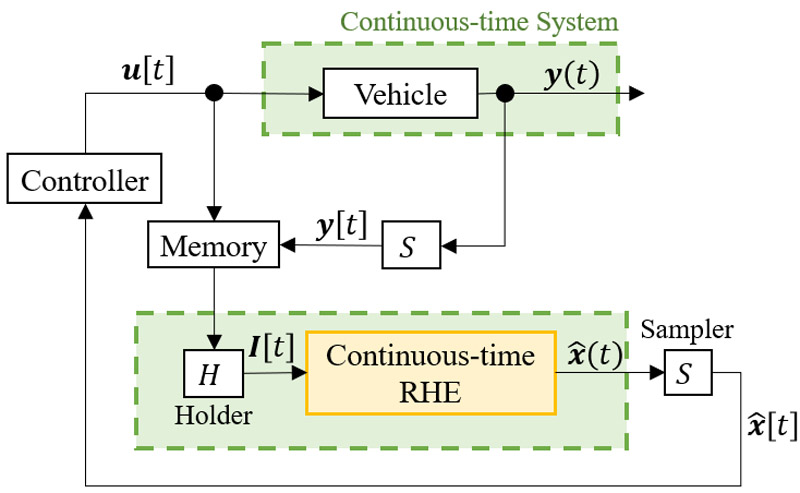
Configuration of continuous-time RHE
- [1] A. Alessandri, M. Baglietto, and G. Battistelli, “Receding-horizon estimation for discrete-time linear systems,” IEEE Trans. on Automatic Control, Vol.48, No.3, pp. 473-478, 2003.
- [2] A. Alessandri, M. Baglietto, and G. Battistelli, “On estimation error bounds for receding-horizon filters using quadratic boundedness,” IEEE Trans. on Automatic Control, Vol.49, No.8, pp. 1350-1355, 2004.
- [3] K. R. Muske, J. B. Rawlings, and J. H. Lee, “Receding horizon recursive state estimation,” 1993 American Control Conf., pp. 900-904. 1993.
- [4] T. Kikuchi, K. Nonaka, and K. Sekiguchi, “Moving horizon estimation with probabilistic data association for object tracking considering system noise constraint,” J. Robot. Mechatron., Vol.32, No.3, pp. 537-547, 2020.
- [5] H. Liu, P. Wang, J. Lin, H. Ding, H. Chen, and F. Xu, “Real-time longitudinal and lateral state estimation of preceding vehicle based on moving horizon estimation,” IEEE Trans. on Vehicular Technology, Vol.70, No.9, pp. 8755-8768, 2021.
- [6] Z. Wang, Z. Liu, and R. Pei, “Estimation of vehicle speed and friction force using moving horizon strategy,” 5th World Congress on Intelligent Control and Automation, Vol.2, pp. 1547-1550, 2004.
- [7] H. Zhao and H. Chen, “Estimation of vehicle yaw rate and side slip angle using moving horizon strategy,” 2006 6th World Congress on Intelligent Control and Automation, pp. 1828-1832, 2006.
- [8] H. Okajima and T. Asai, “Path-following control based on trajectory differences,” IFAC Proc. Volumes, Vol.37, No.11, pp. 701-706, 2004.
- [9] H. Okajima and N. Matsunaga, “Robust path following control based on model error compensator,” Trans. of the Institute of Systems, Control and Information Engineers, Vol.29, No.10, pp. 466-468, 2016 (in Japanese).
- [10] K. Yoshida, M. Inoue, and T. Hatanaka, “Instant MPC for linear systems and dissipativity-based stability analysis,” IEEE Control Systems Letters, Vol.3, No.4, pp. 811-816, 2019.
- [11] T. Miyano, S. Yamashita, T. Hatanaka, K. Shibata, T. Jimbo, and M. Fujita, “Continuous-time optimization dynamics mirroring ADMM architecture and passivity-based robustification against delays,” IEEE Trans. on Control of Network Systems, Vol.7, No.3, pp. 1296-1307, 2020.
- [12] K. Sato, K. Sawada, and M. Inoue, “On the instant iterative learning MPC for nonlinear systems,” 2020 59th Annual Conf. of the Society of Instrument and Control Engineers of Japan (SICE), pp. 1166-1171, 2020.
- [13] K. Sato, K. Sawada, and M. Inoue, “Renzoku jikan algorithm ni yoru senkei model yosoku seigyo to judousei ni motoduku syuusokusei kaiseki [Linear model predictive control via continuous-time optimization algorithm and passivity-based convergence analysis],” The 8th Multi-Symp. on Control Systems (MSCS 2021), 2021 (in Japanese).
- [14] M. Abe, “Automotive Vehicle Dynamics: Theory and Applications,” 2nd Edition, Tokyo Denki University Press, 2012 (in Japanese).
- [15] Y. Matsunaga, T. Inoue, H. Tokunaga, and Y. Nishio, “Rear-wheel independent steering system,” NTN Technical Review, No.83, pp. 26-31, 2015 (in Japanese).
- [16] A. Cherukuri, E. Mallada, and J. Cortés, “Asymptotic convergence of constrained primal-dual dynamics,” Systems & Control Letters, Vol.87, pp. 10-15, 2016.
- [17] S. Yamashita, T. Hatanaka, J. Yamauchi, and M. Fujita, “Passivity-based generalization of primal-dual dynamics for non-strictly convex cost functions,” Automatica, Vol.112, Article No.108712, 2020.
- [18] S. Boyd and L. Vandenberghe, “Convex optimization,” Cambridge University Press, 2004.
- [19] H. Yamamoto and K. Tsumura, “Control of smart grids based on price mechanism and network structure,” Mathematical Engineering Technical Reports, METR 2012-11, The University of Tokyo, 2012.
- [20] J. Lofberg, “YALMIP: A toolbox for modeling and optimization in MATLAB,” 2004 IEEE Int. Conf. on Robotics and Automation, pp. 284-289, 2004.
- [21] J. F. Sturm, “Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones,” Optimization Methods and Software, Vol.11, Nos.1-4, pp. 625-653, 1999.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.