Paper:
MGV Obstacle Avoidance Trajectory Generation Considering Vehicle Shape
Yoshihide Arai, Takashi Sago, Yuki Ueyama, and Masanori Harada
National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
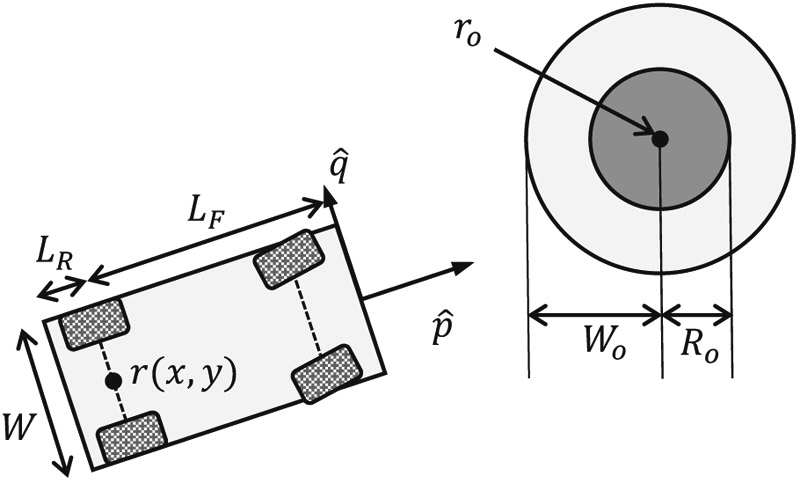
This study investigates the application of obstacle avoidance trajectory generation considering the vehicle shape of a micro ground vehicle by successive convexification and state-triggered constraints. The avoidance trajectory is generated by numerical computation and path-following experiments are conducted to assess the generated trajectory. The numerical computation results indicate that the trajectory obtained by the algorithm successfully avoids obstacles considering the vehicle shape and satisfies the constraints. The experiment includes the model predictive control to follow the generated trajectory. Numerical computations and experiments confirm the usefulness of the trajectory generation algorithm.
Obstacle avoidance by compound STCs
- [1] Y. Kobayashi, M. Kondo, Y. Hiramatsu, H. Fujii, and T. Kamiya, “Mobile Robot Decision-Making Based on Offline Simulation for Navigation over Uneven Terrain,” J. Robot. Mechatron., Vol.30, No.4, pp. 671-682, 2018.
- [2] S. Horiuchi, R. Hirao, K. Okada, and S. Nohtomi, “Optimal Steering and Braking Control in Emergency Obstacle Avoidance,” Trans. of the Japan Society of Mechanical Engineers, C, Vol.72, No.722, pp. 3250-3255, 2006 (in Japanese).
- [3] H. Taghavifar, B. Xu, L. Taghavifar, and Y. Qin, “Optimal Path-Planning of Nonholonomic Terrain Robots for Dynamic Obstacle Avoidance Using Single-Time Velocity Estimator and Reinforcement Learning Approach,” IEEE Access, Vol.7, pp. 159347-159356, 2019.
- [4] L. R. Lewis, I. M. Ross, and Q. Gong, “Pseudospectral motion planning techniques for autonomous obstacle avoidance,” 2007 46th IEEE Conf. on Decision and Control, pp. 5997-6002, 2007.
- [5] Q. Gong, L. R. Lewis, and I. M. Ross, “Pseudospectral Motion Planning for Autonomous Vehicles,” J. of Guidance, Control, and Dynamics, Vol.32, No.3, pp. 1039-1045, 2009.
- [6] S. Watanabe and M. Harada, “Real-Time Optimal Feedback Control of UGVs Using Modified Carathéodory-π Solutions,” Proc. of 12th Int. Symposium on Advanced Vehicle Control, pp. 385-390, 2014.
- [7] M. Szmuk, D. Malyuta, T. P. Reynolds, M. S. Mceowen, and B. Açikmeşe, “Real-Time Quad-Rotor Path Planning Using Convex Optimization and Compound State-Triggered Constraints,” 2019 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 7666-7673, 2019.
- [8] A. Boyali and S. Thompson, “Autonomous Parking by Successive Convexification and Compound State Triggers,” 2020 IEEE 23rd Int. Conf. on Intelligent Transportation Systems (ITSC), pp. 1-8, 2020.
- [9] M. Szmuk, T. Reynolds, B. Acikmese, M. Mesbahi, and J. M. Carson, “Successive convexification for 6-dof powered descent guidance with compound state-triggered constraints,” AIAA Scitech 2019 Forum, Article No.0926, 2019.
- [10] Y. Mao, M. Szmuk, and B. Açıkmeşe, “Successive convexification of non-convex optimal control problems and its convergence properties,” 2016 IEEE 55th Conf. on Decision and Control (CDC), pp. 3636-3641, 2016.
- [11] D. Malyuta, T. P. Reynolds, M. Szmuk, T. Lew, R. Bonalli, M. Pavone, and B. Açıkmeşe, “Convex Optimization for Trajectory Generation: A Tutorial on Generating Dynamically Feasible Trajectories Reliably and Efficiently,” IEEE Control Systems Magazine, Vol.42, No.5, pp. 40-113, 2022.
- [12] A. Domahidi, E. Chu, and S. Boyd, “ECOS: An SOCP solver for embedded systems,” 2013 European Control Conf. (ECC), pp. 3071-3076, 2013.
- [13] M. Grant and S. Boyd, “CVX: Matlab software for disciplined convex programming, version 2.1,” 2014.
- [14] J. Maciejowski, “Predictive Control with Constraints,” Prentice Hall, 2002.
- [15] S. Watanabe and M. Harada, “Optimal Tracking Control of a Micro Ground Vehicle,” J. Robot. Mechatron., Vol.27, No.6, pp. 653-659, 2015.
- [16] S. Watanabe and M. Harada, “Experimental Study on Optimal Tracking Control of a Micro Ground Vehicle,” J. Robot. Mechatron., Vol.29, No.4, pp. 757-765, 2017.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.