Paper:
Analysis of Autonomous Coordination Between Actuators in the Antagonist Musculoskeletal Model
Takahiro Goto*, Yasuhiro Sugimoto*, Daisuke Nakanishi**, Keisuke Naniwa***, and Koichi Osuka*
*Osaka University
2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
14-4 Nishi-ikuma, Matsue, Shimane 690-8518, Japan
***Hokkaido University
Kita 12, Nishi 7, Kita-ku, Sapporo, Hokkaido 060-0812, Japan
The McKibben Pneumatic Actuator (MPA) is well-known as a type of soft actuator. As MPA generates tension only in the direction of compression, it is necessary to construct an antagonistic structure to drive a joint by MPAs and to coordinate antagonized MPAs. Similar to MPA, muscles in animals also generate tension only in the direction of contraction. Some studies have reported that animals utilize tension information to coordinate muscles for various autonomous movements. The purpose of this study is to realize autonomous cooperation between antagonized MPAs by applying tension feedback control and analyzing the mechanism of coordination. For this purpose, we verify the effect of tension feedback control on the 1-DOF pendulum model with antagonized MPAs. First, through numerical simulations, it is confirmed that the tension feedback generates various coordinated movements of antagonized MPAs, and the pendulum exhibits a bifurcation phenomenon based on the phase difference of the inputs of MPAs. Thereafter, we develop an actual experimental machine based on the model and confirm the autonomous cooperation between actual MPAs through verification experiments similar to the numerical simulations.
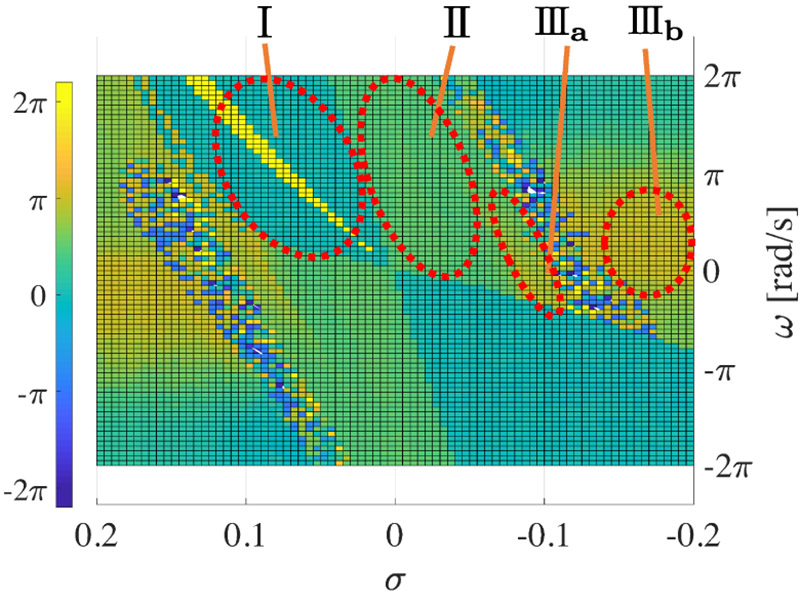
Bifurcation map of coordination patterns between MPAs
- [1] H. Kobayashi, T. Matsushita, Y. Ishida, and K. Kikuchi, “New robot technology concept applicable to human physical support The concept and possibility of the muscle suit (wearable muscular support apparatus),” J. Robot. Mechatron., Vol.14, No.1, pp. 46-53, doi: 10.20965/jrm.2002.p0046, 2002.
- [2] K. Hosoda, Y. Sakaguchi, H. Takayama, and T. Takuma, “Pneumatic-driven jumping robot with anthropomorphic muscular skeleton structure,” Auton. Robots, Vol.28, No.3, pp. 307-316, doi: 10.1007/s10514-009-9171-6, April 2010.
- [3] K. Nakada, T. Asai, and Y. Amemiya, “Biologically-inspired locomotion controller for a quadruped walking robot: Analog IC implementation of a CPG-based controller,” J. Robot. Mechatron., Vol.16, No.4, pp. 397-403, doi: 10.20965/jrm.2004.p0397, 2004.
- [4] G. Taga, Y. Yamaguchi, and H. Shimizu, “Self-organized control of bipedal locomotion by neural oscillators in unpredictable environment,” Biol. Cybern., Vol.65, No.3, pp. 147-159, doi: 10.1007/BF00198086, July 1991.
- [5] G. Liu, M. Habib, K. Watanabe, and K. Izumi, “The design of central pattern generators based on the Matsuoka oscillator to generate rhythmic human-like movement for biped robots,” J. Adv. Comput. Intell. Intell. Inform., Vol.11, No.8, pp. 946-955, 2007.
- [6] Y. Fukuoka, H. Katabuchi, and H. Kimura, “Dynamic locomotion of quadrupeds Tekken3&4 using simple navigation,” J. Robot. Mechatron., Vol.22, No.1, pp. 36-42, doi: 10.20965/jrm.2010.p0036, 2010.
- [7] D. Owaki, T. Kano, K. Nagasawa, A. Tero, and A. Ishiguro, “Simple robot suggests physical interlimb communication is essential for quadruped walking,” J. R. Soc. Interface, Vol.10, No.78, pp. 1-11, doi: 10.1098/rsif.2012.0669, 2013.
- [8] M. A. Gorassini, A. Prochazka, G. W. Hiebert, and M. J. A. Gauthier, “Corrective responses to loss of ground support during walking. I. Intact cats,” J. Neurophysiology, Vol.71, pp. 603-610, doi: 10.1152/jn.1994.71.2.603, 1994.
- [9] G. W. Hiebert, M. A. Gorassini, W. Jiang, A. Prochazka, and K. G. Pearson, “Corrective responses to loss of ground support during walking. II. Comparison of intact and chronic spinal cats,” J. Neurophysiology, Vol.71, pp. 611-622, doi: 10.1152/jn.1994.71.2.611, 1994.
- [10] N. Tsagarakis, “Improved modeling and assessment of pneumatic muscle actuators,” Proc. IEEE Conf. on Robotics and Automation, San Francisco, CA, pp. 3641-3646, doi: 10.1109/ROBOT.2000.845299, 2000.
- [11] B. Tondu and P. Lopez, “Modeling and control of McKibben artificial muscle robot actuators,” IEEE Contr. Syst. Mag., pp. 15-38, doi: 10.1109/37.833638, April 2000.
- [12] S. Yoshida, D. Nakanishi, K. Naniwa, Y. Sugimoto, and K. Osuka, “Verification of linear approximation model of McKibben pneumatic actuator,” Trans. of the JSME, Vol.85, No.878, pp. 1-13, doi: 10.1299/transjsme.18-00498, 2019 (in Japanese).
- [13] Y. Sugimoto, K. Naniwa, K. Osuka, and Y. Sankai, “Static and dynamic properties of McKibben pneumatic actuator for self-stability of legged-robot motion,” Adv. Robotics, Vol.27, No.6, pp. 469-480, doi: 10.1080/01691864.2013.763007, 2013.
- [14] P. Meier, M. Lang, and S. Oberthur, “Reiterated tension testing of silicone elastomer,” Plastics, Rubber and Composites Macromolecular Engineering, Vol.34, No.372-377, doi: 10.1179/174328905X59737, 2005.
- [15] D. Nakanishi, Y. Sugimoto, H. Honda, and K. Osuka, “Measurement experiments and analysis for modeling of McKibben pneumatic actuator,” J. Robot. Mechatron., Vol.28, No.6, pp. 830-836, doi: 10.20965/jrm.2016.p0830, 2016.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.