Paper:
Optimal Position and Attitude Control of Quadcopter Using Stochastic Differential Dynamic Programming with Input Saturation Constraints
Satoshi Satoh*, Hironori Saijo**, and Katsuhiko Yamada*
*Graduate School of Engineering, Osaka University
2-1 Yamadaoka, Suita, Osaka 565-0871, Japan
**Graduate School of Engineering, Kyoto University
Kyotodaigaku-katsura, Nishikyo-ku, Kyoto 615-8246, Japan
This paper considers the position and attitude control of a quadcopter in the presence of stochastic disturbances. Basic quadcopter dynamics is modeled as a nonlinear stochastic system described by a stochastic differential equation. Subsequently, the position and attitude control is formulated as a nonlinear stochastic optimal control problem with input saturation constraints. To solve this problem, a continuous-time stochastic differential dynamic programming (DDP) method with input saturation constraints is newly proposed. Finally, numerical simulations demonstrate the effectiveness of the proposed method by comparing it with the linear quadratic Gaussian and the deterministic DDP with input saturation constraints.
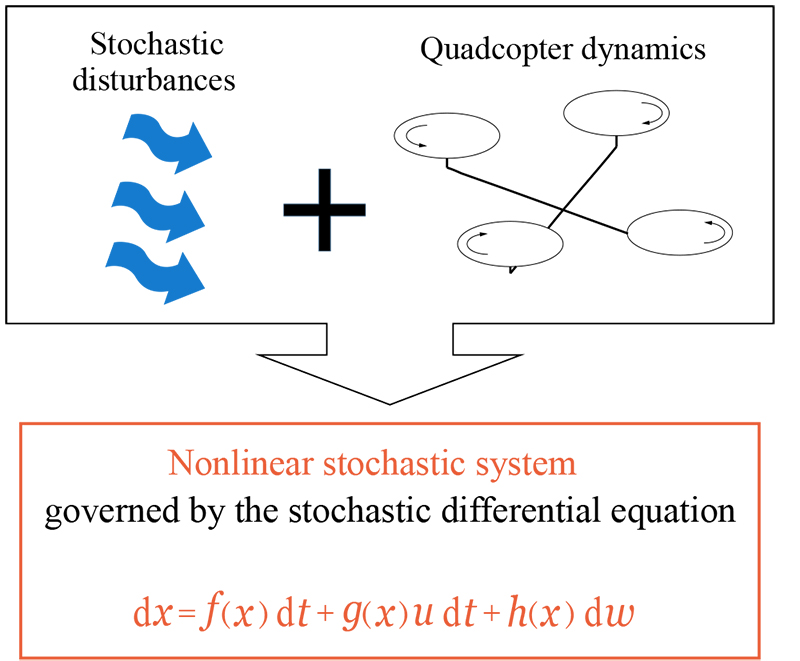
Stochastic system model of a quadcopter
- [1] T. P. Nascimento and M. Saska, “Position and attitude control of multi-rotor aerial vehicles: A survey,” Annual Reviews in Control, Vol.48, pp. 129-146, 2019.
- [2] K. Nonami, F. Kendoul, S. Suzuki, W. Wang, and D. Nakazawa, “Autonomous Flying Robots: Unmanned Aerial Vehicles and Micro Aerial Vehicles,” Springer, 2010.
- [3] G. V. Raffo, M. G. Ortega, and F. R. Rubio, “An integral predictive/nonlinear H-infinity control structure for a quadrotor helicopter,” Automatica, Vol.46, Issue 1, pp. 29-39, 2010.
- [4] A. Castillo, R. Sanz, P. Garcia, W. Qiu, H. Wang, and C. Xu, “Disturbance observer-based quadrotor attitude tracking control for aggressive maneuvers,” Control Engineering Practice, Vol.82, pp. 14-23, 2019.
- [5] A. L’Afflitto, R. B. Anderson, and K. Mohammadi, “An introduction to nonlinear robust control for unmanned quadrotor aircraft: How to design control algorithms for quadrotors using sliding mode control and adaptive control techniques,” IEEE Control Systems Magazine, Vol.38, No.3, pp. 102-121, 2018.
- [6] Y. Kutsuna, M. Ando, and M. Yamada, “Adaptive tracking control of quad-rotor helicopter in quaternion based on input-output linearisation with online estimation of inertia moment,” Int. J. Advanced Mechatronic Systems, Vol.6, No.5, pp. 237-246, 2015.
- [7] E. Capello, F. Quagliotti, and R. Tempo, “Randomized approaches for control of quadrotor UAVs,” J. of Intelligent and Robotic Systems, Vol.73, pp. 157-173, 2014.
- [8] A. Chovancová, T. Fico, L. Chovanec, and P. Hubinský, “Mathematical modelling and parameter identification of quadrotor (a survey),” Procedia Engineering, Vol.96, pp. 172-181, 2014.
- [9] I. Gihman and A. Skorohod, “Stochastic Differential Equations,” Springer-Verlag, 1972.
- [10] N. Ikeda and S. Watanabe, “Stochastic differential equations and diffusion processes,” North-Holland, 1989.
- [11] E. Wong and M. Zakai, “On the convergence of ordinary integrals to stochastic integrals,” Ann. Math. Statist., Vol.36, No.5, pp. 1560-1564, 1965.
- [12] W. H. Fleming and H. M. Soner, “Controlled Markov Processes and Viscosity Solutions,” Springer-Verlag, 2006.
- [13] H. Pham, “Continuous-time Stochastic Control and Optimization with Financial Applications,” Springer-Verlag, 2009.
- [14] H. J. Kappen, “An introduction to stochastic control theory, path integrals and reinforcement learning,” AIP Conference Proc., Vol.887, Issue 1, pp. 149-181, 2007.
- [15] S. Satoh, H. J. Kappen, and M. Saeki, “An iterative method for nonlinear stochastic optimal control based on path integrals,” IEEE Trans. Autom. Contr., Vol.62, No.1, pp. 262-276, 2017.
- [16] E. Theodorou, J. Buchli, and S. Schaal, “A generalized path integral control approach to reinforcement learning,” J. Machine Learning Research, Vol.11, pp. 3153-3197, 2010.
- [17] S. Satoh and H. J. Kappen, “Nonlinear stochastic optimal control with input saturation constraints based on path integrals,” IEEJ Trans. Electrical and Electronic Engineering, Vol.15, Issue 8, pp. 1169-1175, 2020.
- [18] V. Gómez, S. Thijssen, A. Symington, S. Hailes, and H. J. Kappen, “Real-time stochastic optimal control for multi-agent quadrotor swarms,” Proc. of 26th Int. Conf. Automated Planning and Scheduling, pp. 468-476, 2016.
- [19] D. Jacobson and D. Mayne, “Differential Dynamic Programming,” Elsevier, 1970.
- [20] L. Z. Liao and C. A. Shoemaker, “Convergence in unconstrained discrete-time differential dynamic programming,” IEEE Trans. Autom. Contr., Vol.36, No.6, pp. 692-706, 1991.
- [21] C. K. Ng, L. Z. Liao, and D. Li, “A globally convergent and efficient method for unconstrained discrete-time optimal control,” J. Global Optimization, Vol.23, pp. 401-421, 2002.
- [22] S. Satoh, T. Kamiike, and M. Saeki, “Nonlinear stochastic H-infinity control using local quadratic approximation,” Proc. of SICE Int. Symp. on Control Systems 2016, 2A1-5, 2016.
- [23] W. Sun, E. A. Theodorou, and P. Tsiotras, “Stochastic game theoretic trajectory optimization in continuous time,” Proc. of 55th IEEE Conf. on Decision and Control, pp. 6167-6172, 2016.
- [24] E. Theodorou, Y. Tassa, and E. Todorov, “Stochastic differential dynamic programming,” Proc. of American Control Conf., pp. 1125-1132, 2010.
- [25] M. Iwabuchi, S. Satoh, and K. Yamada, “Stabilization of a spacecraft in a halo orbit via differential dynamic programming with input saturation constraints,” Aerospace Technology Japan, 2021 (in press).
- [26] B. Øksendal, “Stochastic differential equations, An introduction with applications,” Springer-Verlag, 1998.
- [27] X. Mao and L. Szpruch, “Strong convergence and stability of implicit numerical methods for stochastic differential equations with non-globally Lipschitz continuous coefficients,” J. Computational and Applied Mathematics, Vol.238, pp. 14-28, 2013.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.