Paper:
Feedback Control for a Drone with a Suspended Load via Hierarchical Linearization
Kazuma Sekiguchi, Wataru Eikyu, and Kenichiro Nonaka
Department of Mechanical Systems Engineering, Faculty of Engineering, Tokyo City University
1-28-1 Tamazutsumi, Setagaya-ku, Tokyo 158-8557, Japan
As a possible extension of a drone application, transportation of a cable-suspended load is expected. The model of a drone with a suspended load is a nonlinear underactuated system that is known to be difficult to analyze and control. This paper applies the linearization method, known as hierarchical linearization, to the system. We observed that, via the hierarchical linearization scheme, the system can be linearized exactly and the controller can be designed simultaneously. There are two features of this approach. First, the controller exactly considers the system nonlinearity, and the feedback controller is based on the linear control theory. Second, it is possible to derive the analytical solution of the closed-loop system. We have demonstrated these features via numerical simulations.
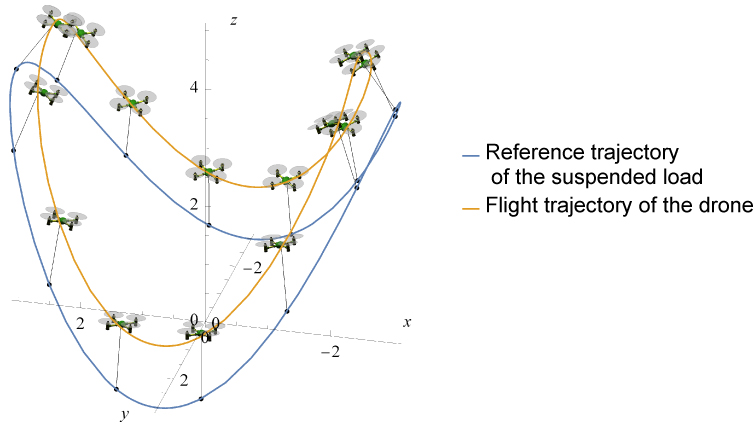
Result snapshots using the proposed controller
- [1] K. Nonami, “Research and development of drone and roadmap to evolution,” J. Robot. Mechatron., Vol.30, No.3, pp. 322-336, 2018.
- [2] X. Ding, P. Guo, K. Xu, and Y. Yu, “A review of aerial manipulation of small-scale rotorcraft unmanned robotic systems,” Chinese J. of Aeronautics, Vol.32, No.1, pp. 200-214, 2019.
- [3] D. K. D. Villa, A. S. Brandão, and M. Sarcinelli-Filho, “A Survey on Load Transportation Using Multirotor UAVs,” J. of Intelligent and Robotic Systems: Theory and Applications, Vol.98, No.2, pp. 267-296, 2020.
- [4] R. Kellermann, T. Biehle, and L. Fischer, “Drones for parcel and passenger transportation: A literature review,” Transportation Research Interdisciplinary Perspectives, Vol.4, 100088, 2020.
- [5] I. Palunko, P. Cruz, and R. Fierro, “Agile load transportation: Safe and efficient load manipulation with aerial robots,” IEEE Robotics and Automation Magazine, Vol.19, No.3, pp. 69-79, 2012.
- [6] K. Sreenath, N. Michael, and V. Kumar, “Trajectory generation and control of a quadrotor with a cable-suspended load – A differentially-flat hybrid system,” 2013 IEEE Int. Conf. on Robotics and Automation, pp. 4888-4895, 2013.
- [7] K. Sreenath, T. Lee, and V. Kumar, “Geometric Control and Differential Flatness of a Quadrotor UAV with a Cable-Suspended Load,” 52nd IEEE Conf. on Decision and Control, pp. 2269-2274, 2013.
- [8] A. Faust, I. Palunko, P. Cruz, R. Fierro, and L. Tapia, “Automated aerial suspended cargo delivery through reinforcement learning,” Artificial Intelligence, Vol.247, pp. 381-398, 2017.
- [9] C. Y. Son, H. Seo, T. Kim, and H. Jin Kim, “Model Predictive Control of a Multi-Rotor with a Suspended Load for Avoiding Obstacles,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 5233-5238, 2018.
- [10] M. Fliess, “Generalized controller canonical form for linear and nonlinear dynamics,” IEEE Trans. on Automatic Control, Vol.35, No.9, pp. 994-1001, 1990.
- [11] M. Fliess, J. Lévine, P. Martin, and P. Rouchon, “Flatness and defect of non-linear systems: introductory theory and examples,” Int. J. of Control, Vol.61, No.6, pp. 1327-1361, 1995.
- [12] M. Fliess, C. Join, and H. Sira-Ramírez, “Non-linear estimation is easy,” Int. J. of Modelling, Identification and Control, Vol.4, No.1, pp. 12-27, 2008.
- [13] K. Sekiguchi, “Stabilization of three-link acrobot via hierarchical linearization,” 54rd IEEE Conf. on Decision and Control, pp. 7808-7813, 2015.
- [14] K. Sekiguchi, “Novel control method for quadcopter-hierarchical linearization approach,” 2017 11th Asian Control Conf., pp. 1853-1858, 2017.
- [15] M. Ishikawa and M. Sampei, “On equlibria set and feedback stabilizability of nonolinear control systems,” IFAC Symposium on Nonlinear Control Systems, pp. 637-642, 1998.
- [16] D. Mellinger and V. Kumar, “Minimum snap trajectory generation and control for quadrotors,” Proc. of IEEE Int. Conf. on Robotics and Automation, pp. 2520-2525, 2011.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.