Paper:
Trajectory Prediction with a Conditional Variational Autoencoder
Thibault Barbié, Takaki Nishio, and Takeshi Nishida
Department of Mechanical and Control Engineering, Kyushu Institute of Technology
1-1 Sensui, Tobata, Kitakyushu, Fukuoka 804-8550, Japan
Conventional motion planners do not rely on previous experience when presented with a new problem. Trajectory prediction algorithms solve this problem using a pre-existing dataset at runtime. We propose instead using a conditional variational autoencoder (CVAE) to learn the distribution of the motion dataset and hence to generate trajectories for use as priors within the traditional motion planning approaches. We demonstrate, through simulations and by using an industrial robot arm with six degrees of freedom, that our trajectory prediction algorithm generates more collision-free trajectories compared to the linear initialization, and reduces the computation time of optimization-based planners.
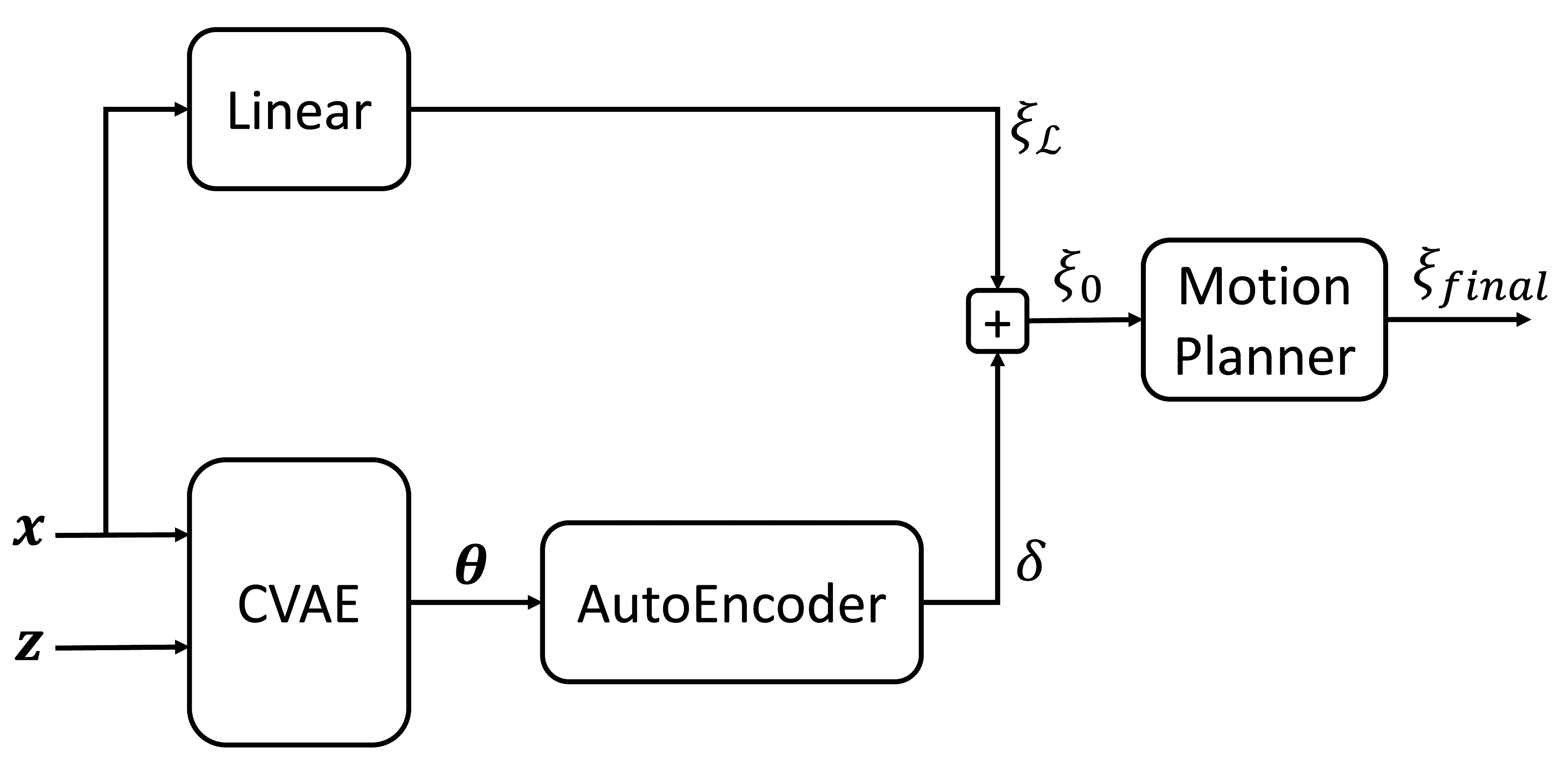
Trajectory prediction using a CVAE
- [1] S. M. LaValle, “Rapidly-exploring random trees: a new tool for path planning,” 1998.
- [2] J. J. Kuffner and S. M. LaValle, “Rrt-connect: an efficient approach to single-query path planning,” Proc. of IEEE Int. Conf. on Robotics and Automation (ICRA’00), Vol.2, pp. 995-1001, 2000.
- [3] S. Karaman and E. Frazzoli, “Sampling-based algorithms for optimal motion planning,” The Int. J. of Robotics Research, Vol.30, No.7, pp. 846-894, 2011.
- [4] N. Ratliff, M. Zucker, J. A. Bagnell, and S. Srinivasa, “CHOMP: Gradient Optimization Techniques for Efficient Motion Planning,” Proc. of IEEE Int. Conf. on Robotics and Automation (ICRA’09), pp. 489-494, 2009.
- [5] M. Kalakrishnan, S. Chitta, E. Theodorou, P. Pastor, and S. Schaal, “STOMP: Stochastic trajectory optimization for motion planning,” Proc. of IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 4569-4574, 2011.
- [6] Z. Marinho, B. Boots, A. Dragan, A. Byravan, G. J. Gordon, and S. Srinivasa, “Functional gradient motion planning in reproducing kernel hilbert spaces,” Proc. of Robotics: Science and Systems, Ann Arbor, Michigan, June 2016.
- [7] B. Kehoe, S. Patil, P. Abbeel, and K. Goldberg, “A survey of research on cloud robotics and automation,” IEEE Trans. Automation Science and Engineering, Vol.12, No.2, pp. 398-409, 2015.
- [8] J. Redmon and A. Farhadi, “YOLO9000: better, faster, stronger,” Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, pp. 7263-7271, 2017.
- [9] Y. Konishi, K. Shigematsu, T. Tsubouchi, and A. Ohya, “Detection of target persons using deep learning and training data generation for Tsukuba challenge,” J. Robot. Mechatron., Vol.30, No.4, pp. 513-522, 2018.
- [10] T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado, and J. Dean, “Distributed representations of words and phrases and their compositionality,” Advances in Neural Information Processing Systems, pp. 3111-3119, 2013.
- [11] D. P. Kingma and M. Welling, “Auto-encoding variational bayes,” arXiv:1312.6114, 2013.
- [12] T. Barbié, R. Kabutan, R. Tanaka, and T. Nishida, “Gaussian mixture spline trajectory: learning from a dataset, generating trajectories without one,” Advanced Robotics, Vol.32, No.10, pp. 547-558, 2018.
- [13] N. Jetchev and M. Toussaint, “Fast motion planning from experience: trajectory prediction for speeding up movement generation,” Autonomous Robots, Vol.34, Nos.1-2, pp. 111-127, 2013.
- [14] D. Berenson, P. Abbeel, and K. Goldberg, “A robot path planning framework that learns from experience,” 2012 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3671-3678, 2012.
- [15] K. Hauser, “Large Motion Libraries: Toward a “Google” for Robot Motions,” Proc. of Robotics Challenges and Vision (RCV2013), 2014.
- [16] B. D. Argall, S. Chernova, M. Veloso, and B. Browning, “A survey of robot learning from demonstration,” Robotics and Autonomous Systems, Vol.57, No.5, pp. 469-483, 2009.
- [17] Y. Duan, M. Andrychowicz, B. Stadie, J. Ho, J. Schneider, I. Sutskever, P. Abbeel, and W. Zaremba, “One-shot imitation learning,” Advances in Neural Information Processing Systems (NIPS 2017), pp. 1087-1098, 2017.
- [18] A. H. Qureshi, M. J. Bency, and M. C. Yip, “Motion planning networks,” arXiv:1806.05767, 2018.
- [19] B. Ichter, J. Harrison, and M. Pavone, “Learning sampling distributions for robot motion planning,” 2018 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 7087-7094, 2018.
- [20] G. E. Hinton and R. R. Salakhutdinov, “Reducing the dimensionality of data with neural networks,” Science, Vol.313, No.5786, pp. 504-507, 2006.
- [21] D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv:1412.6980, 2014.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.