Paper:
Design Method of Spring Balance Mechanism Through Derivation of General Solution
Kazuki Kaneda*, Hirokazu Yamagata**, and Toshio Morita*
*Keio University
3-14-1 Hiyoshi, Kohoku, Yokohama, Kanagawa 223-8522, Japan
**The University of Tokyo
4-6-1 Komaba, Meguro, Tokyo 153-8505, Japan
The present study set out to devise a means of designing a spring-balance mechanism (hereinafter, a SBM) based on a general solution. The goal was to apply a general solution as a guideline for identifying the optimum design solution. A SBM is used to reduce the actuator output in the design of a mechanical device. As a result, the effect of gravity can be offset and energy-saving in operation can be realized. To date, however, SBMs have been designed on a trial and error basis, with a reliance on the designer’s knowledge or experience. Thus, in some instances, it may not be possible to identify a design solution that should, in theory, be achievable. To overcome this issue, this study examined the application of a general solution to the design of a SBM. Such a general solution would identify a solution space including viable design solutions. Subsequently, once a design that satisfies the general solution had been identified, a search could be made of all the design solutions within the solution space. First, the sequence whereby the general solution is used to identify a SBM design that satisfies the general solution, thus providing a guideline for the search action, is determined. Herein, the method used to identify this initial SBM design is presented. The devised method is based on the description of an energy-conservation formula that does not involve any trial and error. The proposed method incorporates a conventional method into the design solution, which can be derived when the conventional method cannot identify a design solution. As a result, a design method using a general solution for the design of an SBM is realized.
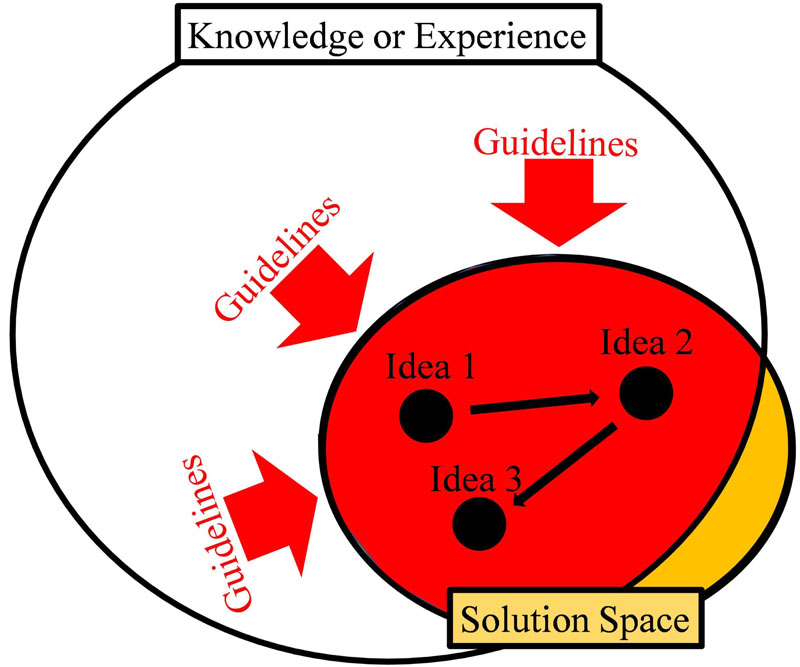
Design method of spring-balance mechanism
- [1] N. Ulrich and V. Kumar, “Passive Mechanical Gravity Compensation for Robot Manipulator,” Proc. of the 1991 IEEE Int. Conf. on Robotics and Automation, Sacramento, pp. 1536-1541, 1991.
- [2] Y. Chheta, R. Joshi, K. Gotewal, and M. Stephen, “A Review on Passive Gravity Compensation,” Proc. of the 2017 IEEE Int. Conf. on Electronics, Communication and Aerospace Technology (ICECA), pp. 184-189, 2017.
- [3] V. Arakelian, “Gravity compensation in robotics,” Advanced Robotics, Vol.30, No.2, pp. 79-96, 2016.
- [4] T. Morita, Y. Siosawa, H. Nakai, Y.Kuribara, and S. Sugano, “A novel mechanism design for gravity compensation in three dimensional space,” Proc. of the 2003 IEEE/ASME Int. Conf. on Advanced Intelligent Mechanics (AIM 2003), pp. 163-168, 2003.
- [5] T. Morita, Y. Siosawa, H. Nakai, Y. Kuribara, and S. Sugano, “Development of third dimension mechanical gravity canceller for high kinematical performance manipulator,” Summary book of Robotics Mechatronics lecture, Vol.2002 (2002), No.Pt.4, pp. 2P1.H03(1)-2P1.H03(2), 2002 (in Japanese).
- [6] Y. Ono and T. Morita, “Vertical Planar Underactuated Manipulation Using a Gravity Compensation Mechanism,” J. Robot. Mechatron., Vol.17, No.5, pp. 553-559, 2005.
- [7] Y. Ono and T. Morita, “An Underactuated Manipulation Method Using a Mechanical Gravity Canceller,” J. Robot. Mechatron., Vol.16, No.6, pp. 563-569, 2004.
- [8] M. Bamdad, “Integrated active and passive gravity compensation method for a cable-actuated elbow rehabilitation Robot,” 2015 3rd RSI Int. Conf. on Robotics and Mechatronics (ICROM), No.15686627, 2015.
- [9] K. A. Wyrobek, E. H. Berger, H. F. M. Van der Loos, and J. K. Salisbury, “Towards a Personal Robotics Development Platform: Rationale and Design of an Intrinsically Safe Personal Robot,” The 2008 IEEE Int. Conf. on Robotics and Automation, pp. 2165-2170, 2008.
- [10] C. H. Cho, W. S. Lee, and S. C. Kang, “Static balancing of a manipulator with hemispherical work space,” Proc. of the 2010 IEEE/ASME Int. Conf. on Advanced Intelligent Mechatronics, pp. 1269-1274, 2010.
- [11] N. Shimizu, T. Sawanobori, K. Sokabe, H. Takada, and K. Nonami, “Fundamentals and Applications, Dynamics of machinery,” Kyoritsu Publication Co., pp. i-ii, 1998.
- [12] D. A. Streit and B. J. Gilmore, “‘Perfect’ Spring Equilibrators for Rotatable Bodies,” Trans. ASME J. Mechanisms, Transmissions, and Automation in Design, Vol.111, No.4, pp. 451-458, 1989.
- [13] C. Cho and S. Kang, “Design of a Static Balancing Mechanism with Unit Gravity Compensators,” 2011 IEEE/RSJ Int. Conf. on Intelligent, pp. 1857-1862, 2011.
- [14] B. Rogier, S. Mark, D. Wouter, and M. W. Boudewijin, “Spring-to-spring balancing as energy-free adjustment method in gravity equilibrators,” J. of Mechanical Design, Vol.133, Issue 6, 061010, 2011.
- [15] Japan Society of Spring Engineers, “Spring,” Maruzen Co., pp. 5-304, 2008.
- [16] N. Takesue, Y. Komoda, H. Murayama, K. Fujiwara, and H. Fujimoto, “Scissor lift with real-time self-adjustment ability based on variable gravity compensation mechanism,” Advanced Robotics, Vol.30, No.15, pp. 1014-1026, 2016.
- [17] N. Takesue, T. Ikematsu, H. Murayama, and H. Fujimoto, “Design and Prototype of Variable Gravity Compensation Mechanism (VGCM),” J. Robot. Mechatron., Vol.23, No.2, pp. 249-257, 2011.
- [18] Y. Yamada and T. Morita, “Mechanical Gravity Canceller with Rocking Slider Crank Mechanism,” Trans. of JSME, pp. 1797-1803, 2010 (in Japanese).
- [19] Y. Akutsu and T. Morita, “Mechanical Gravity Canceller having a Roll Axis between Pitch Axes,” Summary book of Robotics Mechatronics lecture, Vol.2013, No.Pt.4, pp. ROMBUNNO.1A2-P25, 2013 (in Japanese).
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.