Paper:
Passivity-Based Tracking Control for Uncertain Nonlinear Feedback Systems
Ni Bu* and Mingcong Deng**
*College of Automation and Electronic Engineering, Qingdao University of Science and Technology
53 Zhengzhou Road, Qingdao, China
**Graduate School of Engineering, Tokyo University of Agriculture and Technology
2-24-16 Nakacho, Koganei, Tokyo 184-8588, Japan
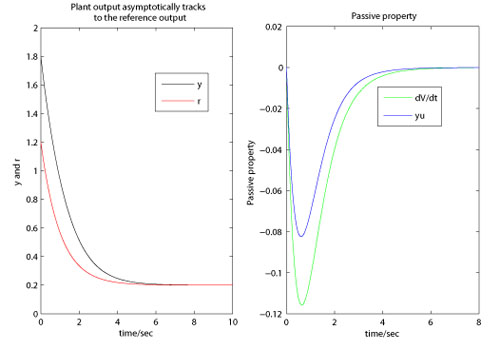
The asymptotic tracking performance and the passivity property
- [1] R. Ortega, A. Loria, P. J. Nicklasson, and H. Sira-Ramirez, “Passivity-based control of Euler-Lagrange Systems,” London, Springer-Verlag, 1998.
- [2] R. Ortega, A. J. van der Schaft, I. Mareels, and B. Maschke, “Putting energy back in control,” IEEE Control System Magazine, Vol.21, pp. 18-23, 2001.
- [3] H. Kojima, T. Hashimoto, and S. Shimoyama, “Trajectory tracking control of a flexible mobile robot using disturbance Observer,” J. of Robotics and Mechatronics, Vol.10, No.3, pp. 272-277, 1998.
- [4] I. Nagai and Y. Tanaka, “Mobile Robot with Floor Tracking Device for Localization and Control,” J. of Robotics and Mechatronics, Vol.19, No.1, pp. 34-41, 2007.
- [5] N. Bu and M. Deng, “System design for nonlinear plants using operator-based robust right coprime factorization and isomorphism,” IEEE Trans. on Automatic Control, Vol.56, pp. 952-957, 2011.
- [6] M. Deng, N. Bu, and A. Inoue, “Output tracking of nonlinear feedback systems with perturbation based on robust right coprime factorization,” Int. J. of Innovative Computing, Information and Control, Vol.5, pp. 3359-3366, 2009.
- [7] A. Wang, D. Wang, H. Wang, S. Wen, and M. Deng, “Nonlinear Perfect Tracking Control for a Robot Arm with Uncertainties Using Operator-Based Robust Right Coprime Factorization Approach,” J. of Robotics and Mechatronics, Vol.27, No.1, pp. 49-56, 2015.
- [8] R. J. P. de Figueiredo and G. R. Chen, “Nonlinear Feedback Control Systems-An Operator Theory Approach,” New York: Academic Press, Inc., 1993.
- [9] M. Deng, A. Inoue, and K. Ishikawa, “Operator-based nonlinear feedback control design using robust right coprime factorization,” IEEE Trans. on Automatic Control, Vol.51, pp. 645-648, 2006.
- [10] M. Deng and N. Bu, “Robust control for nonlinear systems with unknown perturbations using simplified robust right coprime factorization,” Int. J. of Control, Vol.85, pp. 842-850, 2012.
- [11] N. Bu and M. Deng, “Operator-based robust right coprime factorization and nonlinear control scheme for nonlinear plant with unknown perturbations,” Proc. IMechE, Part I-J. Syst. Contr. Engineering, Vol.225, No.6, pp. 760-769, 2011.
- [12] X. Chen, G. Zhai, and T. Fukuda, “An approximate inverse system for nonminimum-phase systems and its application to disturbance observer,” Syst. Control Lett., Vol.52, No.3-4, pp. 193-207, 2004.
- [13] M. Deng and N. Bu, “Robust control for nonlinear systems using passivity-based robust right coprime factorization,” IEEE Trans. on Automatic Control, Vol.57, pp. 2599-2604, 2012.
- [14] N. Bu and M. Deng, “Operator-based robust right coprime factorization and nonlinear control scheme for nonlinear plant with unknown perturbations,” Asian J. Control, Vol.14, No.6, pp. 1655-1661, 2012.
- [15] M. Deng and N. Bu, “Isomorphism-based robust right coprime factorization of nonlinear unstable plants with perturbations,” IET Control Theory and Applications, Vol.4, pp. 2381-2390, 2010.
- [16] N. Bu and X. Liu, “Passivity-based robust control for nonlinear feedback systems using robust right coprime factorization,” Proc. of the 33rd Chinese Control Conf., pp. 2261-2264, 2014.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.