Paper:
FRIT of Internal Model Controllers for Poorly Damped Linear Time Invariant Systems: Kautz Expansion Approach
Hnin Si* and Osamu Kaneko**
*Graduate School of Natural Science and Technology, Kanazawa University
Kakuma-machi, Kanazawa, Ishikawa 920-1192, Japan
**Department of Mechanical Engineering and Intelligent Systems, The University of Electro-Communications
1-5-1 Chofugaoka, Chofu, Tokyo 182-8585, Japan
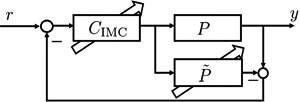
Data-driven approach to internal model controller with tunable parameters
- [1] H. T. Nguyen, O. Kaneko, and S. Yamamoto, “Fictitious Reference Iterative Tuning of Internal Model Controllers for Non-Minimum Phase Systems: A Laguerre Expansion Approach,” SICE J. of Control, Measurement and System Integration, Vol.6, No.1, pp. 38-44, 2012.
- [2] B. Wahlberg, “System Identification using Laguerre Models,” IEEE Trans. on Automatic Control, Vol.36, No.5, pp. 551-562, 1991.
- [3] S. Souma, O. Kaneko, and T. Fujii, “A new method of a controller parameter tuning based on input-output data: Fictitious reference iterative tuning,” Proc. of the 8th IFAC Workshop on Adaptation and Learning in Control and Signal Processing, pp. 789-794, 2004.
- [4] O. Kaneko, “Data-Driven Controller Tuning: FRIT Approach,” Proc. of the 2nd IFAC Workshop on Adaptation and Learning in Control and Signal Processing, pp. 326-336, 2013.
- [5] P. Lindskog and B. Wahlberg, “Application of Kautz Models in System Identifications,” Preprints of the 12th IFAC World Congress, pp. 309-312, 1993.
- [6] B. Wahlberg, “System Identification using Kautz Models,” IEEE Trans. on Automatic Control, Vol.39, No.6, pp. 1276-1282, 1994.
- [7] W. H. Kautz, “Transient Synthesis in the Time Domain,” IRE Trans.-Circuit Theory, Vol CT-1, pp. 29-39, 1954.
- [8] B. Wahlberg and P. M. Makila, “On Approximation of Stable Linear Dynamical Systems using Laguerre and Kautz Functions,” Automatica, Vol.32, No.5, pp. 693-708, 1996.
- [9] O. Kaneko, H. T. Nguyen, Y. Wadagaki, and S. Yamamoto, “Fictitious Reference Iterative Tuning for Non-Minimum Phase Systems in the IMC Architecture: Simultaneous Attainment of Controllers and Models,” SICE J. of Control, Measurement and System Integration, Vol.5, No.2, pp. 101-108, 2012.
- [10] M. G. Safonov and T. C. Tsao, “The Unfalsified Control Concept and Learning,” IEEE Trans. on Automatic and Control, Vol.42, No.6, pp. 843-847, 1997.
- [11] S. Hara and T. Sugie, “Inner-outer factorization for strictly proper functions with jω-axis zeros,” Systems and Control Letters, Vol.16, pp. 179-185, 1991.
- [12] H. Okajima and T. Asai, “Tracking Performance Limitation for 1-DOF Control Systems Using a Set of Attainable Outputs,” SICE J. of Control, Measurement, and System Integration, Vol.8, No.5, pp. 348-353, 2015.
- [13] A. C. den Brinker and H. J. W. Belt, “Using Kautz Model in Model Reduction,” Ch-13, pp. 185-196, Signal Analysis and Prediction, Springer Science+Business Media, 1998.
ISBN: 978-1-4612-7273-1 - [14] S. da Silva, “Non-parametric identification of mechanical systems by Kautz filter with multiple poles,” Mechanical System and Signal Processing Vol.25, Issue 4, pp. 1103-1111, 2011.
- [15] S. da Silva, V. Lope Junior, and M. J. Brennan, “Active Vibration Control using Kautz Filter,” Ch-4, pp. 87-104, doi: http://dx.doi.org/10.5772/50966, 2012.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.