Paper:
Data-Driven Torque Controller for a Hydraulic Excavator
Yasuhito Oshima*1, Takuya Kinoshita*1, Kazushige Koiwai*2, Toru Yamamoto*3, Takao Nanjo*4, Yoichiro Yamazaki*4, and Yoshiaki Fujimoto*4
*1Graduate School of Engineering, Hiroshima University
1-4-1 Kagamiyama, Higashi-hiroshima city, Hiroshima 739-8527, Japan
*2Collaborative Research Division, Institute of Engineering, Hiroshima University
1-4-1 Kagamiyama, Higashi-hiroshima city, Hiroshima 739-8527, Japan
*3Division of Electrical, Systems and Mathematical Engineering, Institute of Engineering, Hiroshima University
1-4-1 Kagamiyama, Higashi-hiroshima city, Hiroshima 739-8527, Japan
*4Global Engineering Center, Kobelco Construction Machinery Co., Ltd.
2-2-1 Itsukaichikou, Saeki-ku, Hiroshima city, Hiroshima 731-5161, Japan
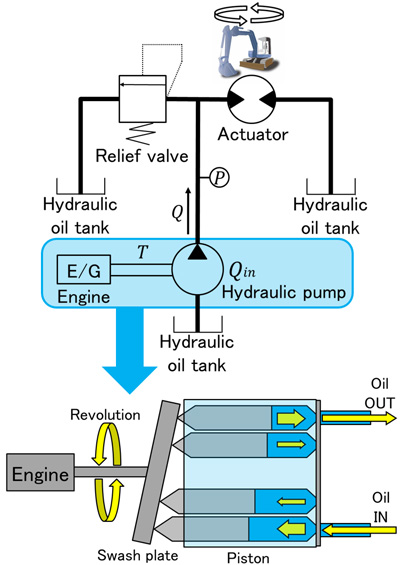
Hydraulic system in the excavator
- [1] S. Okabe, “A Complete Work in Hydraulic Excavator,” Japan Industrial Publishing Co., Ltd., 2007 (in Japanese).
- [2] H. Inoue and H. Yoshida, “Development of Hybrid Hydraulic Excavators,” Int. J. of Automation Technology, Vol.6, No.4, pp. 516-520, 2012.
- [3] S. Ashizawa, T. Watanabe, Y. Kamiya, H. Aoki, and T. Oomichi, “Development of the Energy Simulator for the Water Hydraulic System Under Flow Condition Changes,” J. of Robotics and Mechatronics, Vol.23, No.3, pp. 416-425, 2011.
- [4] H. Yamada, K. Takeichi, and T. Mato, “Sliding Mode Control of Hydraulic Power Shovel,” J. of Robotics and Mechatronics, Vol.15, No.1, pp. 47-53, 2002.
- [5] T. Ohgi and Y. Yokokohji, “Control of Hydraulic Actuator Systems Using Feedback Modulator,” J. of Robotics and Mechatronics, Vol.20, No.5, pp. 47-53, 2008.
- [6] M. Ping, Z. Qian, and L. Nannan, “Study of a Dynamic Predictive PID Control Algorithm,” 2015 Fifth Int. Conf. on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), pp. 1418-1423, 2015.
- [7] J. Guo, G. Wu, and S. Guo, “Fuzzy PID algorithm-based motion control for the spherical amphibious robot,” 2015 IEEE Int. Conf. on Mechatronics and Automation (ICMA), pp. 1583-1588, 2015.
- [8] T. Tateno and H. Nakazawa, “Advanced motion control: From classical PID to nonlinear adaptive robust control,” 2010 11th IEEE Int. Workshop on Advanced Motion Control, pp. 815-829, 2010.
- [9] T. Yamamoto, K. Takao, and T. Yamada, “Design of a Data-Driven PID Controller,” IEEE Trans. on control system Technology, Vol.17, No.1, pp. 29-39, 2009.
- [10] S. Hou and S. Jin, “A Novel Data-Driven Control Approach for a Class of Discrete-Time Nonlinear Systems,” IEEE Trans. on control system, Vol.19, No.6, pp. 1549-1558, 2011.
- [11] R. Thawonmas, M. Iwata, and S. Fukunaga, “A Novel Parallel Model for Self-Organizing Map and its Efficient Implementation on a Data-Driven Multiprocessor,” J. of Advanced Computational Intelligence and Intelligent Informatics, Vol.7, No.3, pp. 355-361, 2003.
- [12] M. Miska and M. Kuwahara, “Sustainable management of data driven projects,” 2010 13th Int. IEEE Conf. on Intelligent Transportation Systems (ITSC), pp. 689-693, 2010.
- [13] M. Dikmen, D. Hoisen, and T. S. Huang, “A data driven method for feature transformation,” 2012 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), pp. 3314-3321, 2012.
- [14] N. N. Nandola and D. E. Rivera, “Model-on-Demand predictive control for nonlinear hybrid systems with application to adaptive behavioral interventions,” 2010 49th IEEE Conf. on Decision and Control (CDC), pp. 6113-6118, 2010.
- [15] S. Wakitani, T. Nawachi, G. R. Martins, and T. Yamamoto, “Design and Implementation of a Data-Oriented Nonlinear PID Controller,” J. of Advanced Computational Intelligence and Intelligent Informatics, Vol.17, No.5, pp. 690-698, 2013.
- [16] S. Masuda, M. Kano, and Y. Yasuda, “A fictitious reference iterative tuning method with simultaneous delay parameter tuning of the reference model,” Int. Conf. on Networking, Sensing and Control 2009 (ICNSC ’09), pp. 422-427, 2009.
- [17] M. Kano, K. Tasaka, M. Ogawa, and A. Takinami, “Extended fictitious reference iterative tuning and its application to chemical processes,” 2011 Int. Symposium on Advanced Control of Industrial Processes (ADCONIP), pp. 379-384, 2011.
- [18] O. Kaneko, S. Souma, and T. Fujii, “A fictitious reference iterative tuning (frit) in the two-degree of freedom control scheme and its application to closed loop system identification,” Proc. of 16th IFAC World congress (CD-ROM), 2005.
- [19] O. Kaneko, “Fictitious reference iterative tuning of internal model controllers for a class of nonlinear systems,” 2015 IEEE Conf. on Control Applications (CCA), pp. 88-94, 2005.
- [20] S. Wakitani, K. Nishida, M. Nakamoto, and T. Yamamoto, “Design of a Data-Driven PID Controller Using Operating Data,” 11th IFAC Int. Workshop on Adaptation and Learning in Control and Signal Processing, pp. 587-592, 2013.
- [21] S. Wakitani and T. Yamamoto, “Design and application of a data-driven PID controller,” IEEE Conf. on Control Applications (CCA), pp. 1443-1448, 2014.
- [22] S. Masuda, “Data-driven PID gain tuning for liquid level control of a single tank based on disturbance attenuation fictitious reference iterative tuning,” 2015 15th Int. Conf. on Control, Automation and Systems (ICCAS), pp. 16-20, 2014.
- [23] H. T. Nguyen, O. Kaneko, and S. Yamamoto, “Data-driven parameter tuning of IMC for unstable plants,” 2012 2nd Australian Control Conf. (AUCC), pp. 92-97, 2012.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.