Top > JRM > Self-Tuning Generalized Minimum Variance Control Based on On-D ...

single-rb.php

JRM Vol.28 No.5 pp. 674-680
doi: 10.20965/jrm.2016.p0674
(2016)

Paper:

Views over last 60 days: 1,344

Self-Tuning Generalized Minimum Variance Control Based on On-Demand Type Feedback Controller

Akira Yanou, Mamoru Minami, and Takayuki Matsuno

Graduate School of Natural Science and Technology, Okayama University
3-1-1 Tsushimanaka, Kita-ku, Okayama 700-8530, Japan

Received:
February 19, 2016
Accepted:
June 5, 2016
Published:
October 20, 2016
Creative Commons License
Keywords:
on-demand type feedback control, coprime factorization, generalized minimum variance control, self-tuning control
Abstract
This paper proposes a design method of self-tuning generalized minimum variance control based on on-demand type feedback controller. A controller, such as generalized minimum variance control (GMVC), generalized predictive control (GPC) and so on, can be extended by using coprime factorization. Then new design parameter is introduced into the extended controller, and the parameter can re-design the characteristic of the extended controller, keeping the closed-loop characteristic that way. Although strong stability systems can be obtained by the extended controller in order to design safe systems, focusing on feedback signal, the extended controller can adjust the magnitude of the feedback signal. That is, the proposed controller can drive the magnitude of the feedback signal to zero if the control objective was achieved. In other words the feedback signal by the proposed method can appear on demand of achieving the control objective. Therefore this paper proposes on-demand type feedback controller using self-tuning GMVC for plant with uncertainty. A numerical example is shown in order to check the characteristic of the proposed method.
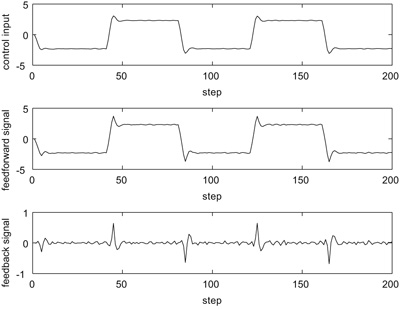
Feedback signal is generated on demand

Feedback signal is generated on demand

Cite this article as:
A. Yanou, M. Minami, and T. Matsuno, “Self-Tuning Generalized Minimum Variance Control Based on On-Demand Type Feedback Controller,” J. Robot. Mechatron., Vol.28 No.5, pp. 674-680, 2016.
Data files:
References
  1. [1] D. W. Clarke, M. A. D. Phil, and P. J. Gawthrop, “Self-tuning control,” Proc. IEE, Vol.126, No.6, pp. 633-640, 1979.
  2. [2] A. Inoue, A. Yanou, and Y. Hirashima, “A Design of a strongly Stable Self-Tuning Controller Using Coprime Factorization Approach,” Preprints of the 14th IFAC World Congress, Vol.C, pp. 211-216, 1999.
  3. [3] A. Inoue, A. Yanou, T. Sato, and Y. Hirashima, “An Extension of Generalized Minimum Variance Control for Multi-input Multi-output Systems Using Coprime Factorization Approach,” Proc. of the American Control Conf., pp. 4184-4188, 2000.
  4. [4] M. Vidyasagar, “Control System Synthesis: A Factorization Approach,” The MIT Press, 1985.
  5. [5] A. Wang, D. Wang, H. Wang, S. Wen, and M. Deng, “Nonlinear Perfect Tracking Control for a Robot Arm with Uncertainties Using Operator-Based Robust Right Coprime Factorization Approach,” J. of Robotics and Mechatronics, Vol.27, No.1, pp. 49-56, 2015.
  6. [6] D. Wang, F. Li, S. Wen, X. Qi, P. Liu, and M. Deng, “Operator-Based Sliding-Mode Nonlinear Control Design for a Process with Input Constraint,” J. of Robotics and Mechatronics, Vol.27, No.1, pp. 83-90, 2015.
  7. [7] A. Yanou, A. Inoue, and Y. Hirashima, “An Extension of Discrete-time Model Reference Adaptive Control by Using Coprime Factorization Approach,” Proc. CCA/CACSD 2002, pp. 606-610, 2002.
  8. [8] A. Yanou and A. Inoue, “An Extension of Multivariable Continuous-time Generalized Predictive Control by using Coprime Factorization Approach,” Proc. SICE Annual Conf. 2003 in Fukui, pp. 3018-3022, 2003.
  9. [9] A. Yanou, A. Inoue, M. Deng, and S. Masuda, “An Extension of Two Degree-of-Freedom of Generalized Predictive Control for M-input M-output Systems Based on State Space Approach,” Int. J. of Innovative Computing, Information and Control (Special Issue on New Trends in Advanced Control and Applications), Vol.4, No.12, 2008.
  10. [10] A. Yanou, M. Deng, and A. Inoue, “A Design of a Strongly Stable Generalized Minimum Variance Control Using a Genetic Algorithm,” Proc. ICROS-SICE Int. Joint Conf. 2009, pp. 1300-1304, 2009.
  11. [11] A. Inoue, T. Henmi, and M. Deng, “Strongly Stable GPC with Suppression of Steady State Gain and Closed-loop Poles,” Proc. of the 2015 Int. Conf. on Advanced Mechatronic Systems, pp. 322-327, 2015.
  12. [12] A. Yanou, M. Minami, and T. Matsuno, “A Design Method of Self-Tuning Controller Using Strongly Stable Rate,” Proc. SICE SSI2013, pp. 663-667, 2013.
  13. [13] A. Yanou, M. Minami, and T. Matsuno, “Strong Stability Rate for Control Systems using Coprime Factorization,” Trans. of the Society of Instrument and Control Engineers, Vol.50, No.5, pp. 441-443, 2014.
  14. [14] A. Yanou, M. Minami, and T. Matsuno, “Safety Assessment of Self-tuning Generalized Minimum Variance Control by Strong Stability Rate,” IEEJ Trans. on Electronics, Information and Systems, Vol.134, No.9, pp. 1241-1246, 2014.
  15. [15] A. Yanou, M. Minami, and T. Matsuno, “A Design Method of On-Demand Type Feedback Controller Using Coprime Factorization,” Proc. of the 10th Asian Control Conf. 2015, 2015.
  16. [16] S. Okazaki, J. Nishizaki, A. Yanou, M. Minami, and M. Deng, “Strongly Stable Generalized Predictive Control Focused on Closed-loop Characteristics,” Trans. of the Society of Instrument and Control Engineers, Vol.47, No.7, pp. 317-325, 2011.
  17. [17] T. Yamamoto, Y. Sakawa, and S. Omatu, “A Construction of Pole-Assignment Self-Tuning Control System,” Trans. of the Society of Instrument and Control Engineers, Vol.30, No.3, pp. 285-294, 1994.
  18. [18] S. Omatu and T. Yamamoto (Ed.), “Self-Tuning Control,” SICE, 1996 (in Japanese).

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Oct. 11, 2024