Top > JRM > Nonlinear Perfect Tracking Control for a Robot Arm with Uncert ...

single-rb.php

JRM Vol.27 No.1 pp. 49-56
doi: 10.20965/jrm.2015.p0049
(2015)

Paper:

Views over last 60 days: 1,460

Nonlinear Perfect Tracking Control for a Robot Arm with Uncertainties Using Operator-Based Robust Right Coprime Factorization Approach

Aihui Wang*, Dongyun Wang*, Haiquan Wang*, Shengjun Wen*, and Mingcong Deng**

*School of Electric and Information Engineering, Zhongyuan University of Technology
41 Zhongyuan Road, Zhengzhou 450007, China

**Graduate School of Engineering, Tokyo University of Agriculture and Technology
2-24-16 Nakacho, Koganei, Tokyo 184-8588, Japan

Received:
April 13, 2014
Accepted:
December 18, 2014
Published:
February 20, 2015
Creative Commons License
Keywords:
operator, robust right coprime factorization, robust nonlinear control, perfect tracking
Abstract
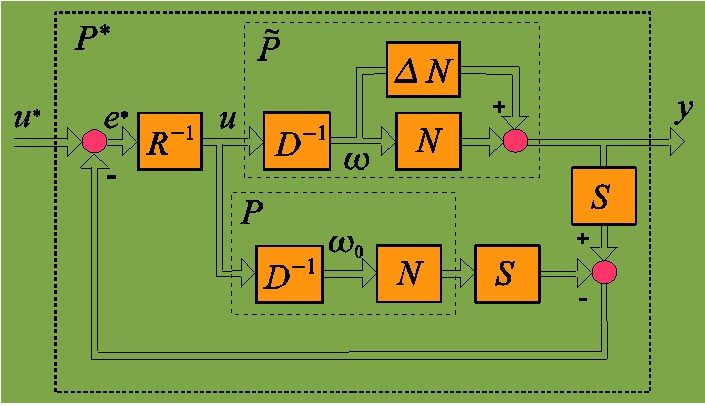Plant uncertainties compensation
In this paper, a robust nonlinear perfect tracking control for a robot arm with uncertainties is proposed by using operator-based robust right coprime factorization approach. In general, there exist unknown modelling errors in measuring structural parameters of the robot arm and external disturbances in real situations. In the present control system design, the effect of the modelling errors and disturbances on the system performance is considered to be uncertainties of the robot arm dynamics. Considering the uncertainties, a robust nonlinear perfect tracking control using operator-based robust right coprime factorization is investigated. That is, first, considering the unknown uncertain plant generates limitations in obtaining the so-called universal stability and tracking conditions, the effect of uncertain plant is compensated by designed operator-based feedback control scheme. Second, a new perfect tracking condition is proposed for improving the trajectory of the robot arm. Finally, the effectiveness of the designed system is confirmed by simulation results.
Cite this article as:
A. Wang, D. Wang, H. Wang, S. Wen, and M. Deng, “Nonlinear Perfect Tracking Control for a Robot Arm with Uncertainties Using Operator-Based Robust Right Coprime Factorization Approach,” J. Robot. Mechatron., Vol.27 No.1, pp. 49-56, 2015.
Data files:
References
  1. [1] F. L. Lewis, D. M. Dawson, and C. T. Abdallah, “Robot Manipulator Control: Theory and Practice,” Marcel Dekker, Inc., 2004.
  2. [2] N. Hogan, “Impedance control of industrial robots,” Robotics & Computer-Integrated Manufacturing, Vol.1, No.1, pp. 97-113, 1984.
  3. [3] R. Richardson, M. Brown, B. Bhakta, and M. Levesley, “Impedance control for a pneumatic robot-based around pole-placement, joint space controllers,” Control Engineering Practice, Vol.13, No.3, pp. 291-303, 2005.
  4. [4] S. Islam and X. Liu, “Robust sliding mode control for robot manipulators,” IEEE Trans. on Industrial Electronics, Vol.58, No.6, pp. 2444-2453, 2011.
  5. [5] C. S. Kim, E. J. Mo, S. M. Han, M. S. Jie, and K. W. Lee, “Robust visual servo control of robot manipulators with uncertain dynamics and camera parameters,” Int. J. of Control, Automation, and Systems, Vol.8, No.2, pp. 308-313, 2010.
  6. [6] A. A. Ata, “Optimal trajectory planning of manipulators: a review,” J. of Engineering Science and Technology, Vol.2, No.1, pp. 32-54, 2007.
  7. [7] G. Simmons and Y. Demiris, “Optimal robot arm control using the minimum variance model,” J. of Robotic Systems, Vol.22, No.11, pp. 677-690, 2005.
  8. [8] V. Arakelian, J. L. Baron, and P. Mottu, “Torque minimisation of the 2-DOF serial manipulators based on minimum energy consideration and optimum mass redistribution,” Mechatronics, Vol.21, No.1, pp. 310-314, 2011.
  9. [9] S. Devasia, “Nonlinear minimum-time control with pre- and post-actuation,” Automatica, Vol.47, No.7, pp. 1379-1387, 2011.
  10. [10] P. Tomei, “Adaptive PD controller for robot manipulators,” IEEE Trans. on Robotics and Automation, Vol.7, No.4, pp. 565-570, 1991.
  11. [11] C. Chiena and A. Tayebib, “Further results on adaptive iterative learning control of robot manipulators,” Automatica, Vol.44, No.3, pp. 830-837, 2008.
  12. [12] H. Le, S. Lee, and C. Lee, “Integration model reference adaptive control and exact linearization with disturbance rejection for control of robot manipulators,” Int. J. of Innovative Computing, Informa-tion and Control, Vol.7, No.6, pp. 3255-3268, 2011.
  13. [13] K. Althoefer, B. Krekelberg, D. Husmeier, and L. Seneviratne, “Reinforcement learning in a rule-based navigator for robotic manipulators,” Neurocomputing, Vol.37, No.1-4, pp. 51-70, 2011.
  14. [14] C. T. Freeman, P. L. Lewin, E. Rogers, and J. D. Ratcliffe, “Iterative learning control applied to a gantry robot and conveyor system,” Trans. of the Institute of Measurement and Control, Vol.32, No.3, pp. 251-264, 2010.
  15. [15] N. Kumara, V. Panwarb, N. Sukavanamc, S. P. Sharmac, and J. H. Borma, “Neural network-based nonlinear tracking control of kinematically redundant robot manipulators,” Mathematical and Computer Modelling, Vol.53, No.9-10, pp. 1889-1901, 2011.
  16. [16] T. Sun, H. Pei, Y. Pan, H. Zhou, and C. Zhang, “Neural network-based sliding mode adaptive control for robot manipulators,” Neurocomputing, Vol.74, No.14-15, pp. 2377-2384, 2011.
  17. [17] C. C. Cheng, S. H. Chien, and F. C. Shih, “Design of robust adaptive variable structure tracking controllers with application to rigid robot manipulators,” IET Control Theory & Applications, Vol.4, No.9, pp. 1655-1664, 2010.
  18. [18] F. Moldoveanu, V. Comnac, D. Floroian, and C. Boldisor, “Trajectory tracking control of a two-link robot manipulator using variable structure system theory,” Control Engineering and Applied Informatics, No.7, No.3, pp. 56-62, 2005.
  19. [19] T. Henmi, T. Ohta, M. Deng, and A. Inoue, “Tracking control of a twolink planar manipulator using nonlinear model predictive control,” Int. J. of Innovative Computing, Information and Control, Vol.6, No.7, pp. 2977-2984, 2010.
  20. [20] C. P. Tan, X. Yu, and Z. Man, “Terminal sliding mode observers for a class of nonlinear systems,” Automatica, Vol.46, No.8, pp. 1401-1404, 2010.
  21. [21] S. Islam and X. P. Liu, “Robust sliding mode control for robot manipulators,” IEEE Trans. on Industrial Electronics, Vol.58, No.6, pp. 2444-2453, 2011.
  22. [22] W. E. Dixon, M. S. de Queiroz, F. Zhang, and D. M. Dawson, “Tracking control of robot manipulators with bounded torque inputs,” Robotica, Vol.17, No.2, pp. 121-129, 1999.
  23. [23] Y. Oh and W. K. Chung, “Disturbance-observer-based motion control of redundant manipulators using inertially decoupled dynamics,” IEEE Trans. on Mechatronics, Vol.4, No.2, pp. 133-146, 1999.
  24. [24] P. Herman and D. Franelak, “Robust tracking controller with constraints using generalized velocity components for manipulators,” Trans. of the Institute of Measurement and Control, Vol.30, No.2, pp. 101-113, 2008.
  25. [25] R. Fukui, H. Morishita, and T. Sato, “Experimental comparison of two ceiling hanging mobile robots through real prototypes development,” J. Robotics and Mechatronics, Vol.26, No.1, pp. 40-50, 2014.
  26. [26] X. Dai, Z. Yao, and Y. Zhao, “A discrete adaptive auction-based algorithm for task assignments of multi-robot systems,” J. Robotics and Mechatronics, Vol.26, No.3, pp. 369-376, 2014.
  27. [27] S. Hashimoto, A. Ishida, M. Inami, and T. Igarashi, “TouchMe: an augmented reality interface for remote robot control,” J. Robotics and Mechatronics, Vol.25, No.3, pp. 527-537, 2014.
  28. [28] A. Wang and M. Deng, “Robust nonlinear control design to a manipulator based on operator based approach,” ICIC Express Letters, Vol.6, No.3, pp. 617-623, 2012.
  29. [29] A. Wang and M. Deng, “Robust nonlinear multivariable tracking control design to a manipulator with unknown uncertainties using operator-based robust right coprime factorization,” Trans. of the Institute of Measurement and Control, Vol.35, No.6, pp. 788-797, 2013.
  30. [30] A. Wang and M. Deng, “Operator-based robust nonlinear tracking control for a human multi-joint arm-like manipulator with unknown time-varying delays,” Applied Mathematics & Information Sciences, Vol.6, No.3, pp. 459-468, 2012.
  31. [31] A. Wang, M. Deng, and D. Wang, “Operator-based robust control design for a human arm-like manipulator with time-varying delay measurements,” Int. J. of Control, Automation, and Systems, Vol.11, No.6, pp. 1112-1121, 2013.
  32. [32] A. Banos, “Stabilization of nonlinear systems based on a generalized Bezout identity,” Automatica, Vol.32, No.4, pp. 591-595, 1996.
  33. [33] M. Deng, A. Inoue, and K. Ishikawa, “Operator-based nonlinear feedback control design using robust right coprime factorization,” IEEE Trans. on Automatic Control, Vol.51, No.4, pp. 645-648, 2006.
  34. [34] N. Bu and M. Deng, “System design for nonlinear plants using operator-based robust right coprime factorization and isomorphism,” IEEE Trans. on Automatic Control, Vol.56, No.4, pp. 952-957, 2011.
  35. [35] M. Deng, S. Bi, and A. Inoue, “Robust nonlinear control and tracking design for multi-input multi-output nonlinear perturbed plants,” IET Control Theory & Applications, Vol.3, No.9, pp. 1237-1248, 2009.
  36. [36] T. Yoshikawa, “Foundations of robotics: analysis and control,” The MIT Press, 1990.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on Feb. 13, 2025