Paper:
Jensen–Shannon Divergence-Based k-Medoids Clustering
Yuto Kingetsu* and Yukihiro Hamasuna**
*Graduate School of Science and Engineering, Kindai University
3-4-1 Kowakae, Higashiosaka, Osaka 577-8502, Japan
**Department of Informatics, School of Science and Engineering, Kindai University
3-4-1 Kowakae, Higashiosaka, Osaka 577-8502, Japan
Several conventional clustering methods use the squared L2-norm as the dissimilarity. The squared L2-norm is calculated from only the object coordinates and obtains a linear cluster boundary. To extract meaningful cluster partitions from a set of massive objects, it is necessary to obtain cluster partitions that consisting of complex cluster boundaries. In this study, a JS-divergence-based k-medoids (JSKMdd) is proposed. In the proposed method, JS-divergence, which is calculated from the object distribution, is considered as the dissimilarity. The object distribution is estimated from kernel density estimation to calculate the dissimilarity based on both the object coordinates and their neighbors. Numerical experiments were conducted using five artificial datasets to verify the effectiveness of the proposed method. In the numerical experiments, the proposed method was compared with the k-means clustering, k-medoids clustering, and spectral clustering. The results show that the proposed method yields better results in terms of clustering performance than other conventional methods.
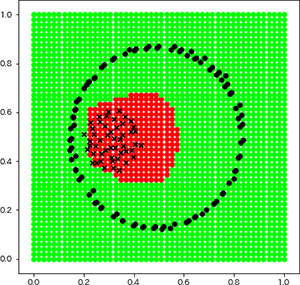
Experimentally determined cluster boundary by the proposed method JSKMdd
- [1] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering,” Springer, 2008.
- [2] A. K. Jain, “Data clustering: 50 years beyond K-means,” Pattern Recognition Letters, Vol.31, No.8, pp. 651-666, 2010.
- [3] B. Schölkopf and A. J. Smola, “Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond,” MIT Press, 2001.
- [4] M. Girolami, “Mercer kernel-based clustering in feature space,” IEEE Trans. Neural Networks, Vol.13, No.3, pp. 780-784, 2002.
- [5] Y. Endo, H. Haruyama, and T. Okubo, “On some hierarchical clustering algorithms using kernel functions,” Proc. of IEEE Int. Conf. on Fuzzy Systems (FUZZ-IEEE 2004), pp. 1513-1518, 2004.
- [6] D. E. Gustafson and W. C. Kessel, “Fuzzy clustering with a fuzzy covariance matrix,” Proc. of IEEE Conf. on Decision and Control, pp. 761-766, 1979.
- [7] R. N. Davé and R. Krishnapuram, “Robust clustering methods : A unified view,” IEEE Trans. on Fuzzy Systems, Vol.5, No.2, pp. 270-293, 1997.
- [8] Y. Hamasuna and Y. Endo, “On semi-supervised fuzzy c-means clustering for data with clusterwise tolerance by opposite criteria,” Soft Computing, Vol.17, No.1, pp. 71-81, 2013.
- [9] Y. Endo, Y. Hamasuna, T. Hirano, and N. Kinoshita, “Even-Sized Clustering Based on Optimization and its Variants,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.1, pp. 62-69, doi: 10.20965/jaciii.2018.p0062, 2018.
- [10] R. J. G. B. Campello, D. Moulavi, and J. Sander, “Density-based clustering based on hierarchical density estimates,” Proc. of Pacific-Asia Conference on Knowledge Discovery and Data Mining (PAKDD 2013), Lecture Notes in Computer Science, Vol.7819, pp. 160-172, 2013.
- [11] M. Ester, H.-P. Kriegel, J. Sander, and X. Xu, “A density-based algorithm for discovering clusters in large spatial databases with noise,” Proc. of the 2nd Int. Conf. on Knowledge Discovery and Data Mining (KDD’96), pp. 226-231, 1996.
- [12] M. M. Breunig, H.-P. Kriegel, R. T. Ng, and J. Sander, “LOF: identifying density-based local outliers,” Proc. of the 2000 ACM SIGMOD Int. Conf. on Management of Data (SIGMOD ’00), pp. 93-104, 2000.
- [13] Y. Hamasuna, Y. Kingetsu, and S. Nakano, “k-medoids clustering based on kernel density estimation and Jensen-Shannon divergence,” Proc. of Modeling Decisions for Artificial Intelligence (MDAI 2019), Lecture Notes in Computer Science, Vol.11676, pp. 272-282, 2019.
- [14] V. A. Epanechnikov, “Non-parametric estimation of a multivariate probability density,” Theory of Probability and its Application, Vol.14, pp. 153-158, 1969.
- [15] B. Fuglede and F. Topsoe, “Jensen-Shannon divergence and Hilbert space embedding,” Proc. Int. Symp. on Information Theory (ISIT 2004), 2004.
- [16] L. Kaufman and P. J. Rousseeuw, “Finding Groups in Data: An Introduction to Cluster Analysis,” Wiley, 1990.
- [17] L. Hubert and P. Arabie, “Comparing Partitions,” J. of Classification, Vol.2, No.1, pp. 193-218, 1985.
- [18] S. Kullback and R. A. Leibler, “On information and sufficiency,” Annals of Mathematical Statistics, Vol.22, pp. 79-86, 1951.
- [19] U. von Luxburg, “A tutorial on spectral clustering,” Statistics and Computing, Vol.17, No.4, pp. 395-416, 2007.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.