Paper:
A Fast Method for Fuzzy Rules Learning with Derivative-Free Optimization by Formulating Independent Evaluations of Each Fuzzy Rule
Kiyohiko Uehara* and Kaoru Hirota**
*Ibaraki University
4-12-1 Nakanarusawa-cho, Hitachi, Ibaraki 316-8511, Japan
**Beijing Institute of Technology
No.5 South Street, Zhongguancun, Haidian District, Beijing 100081, China
A method is proposed for evaluating fuzzy rules independently of each other in fuzzy rules learning. The proposed method is named α-FUZZI-ES (α-weight-based fuzzy-rule independent evaluations) in this paper. In α-FUZZI-ES, the evaluation value of a fuzzy system is divided out among the fuzzy rules by using the compatibility degrees of the learning data. By the effective use of α-FUZZI-ES, a method for fast fuzzy rules learning is proposed. This is named α-FUZZI-ES learning (α-FUZZI-ES-based fuzzy rules learning) in this paper. α-FUZZI-ES learning is especially effective when evaluation functions are not differentiable and derivative-based optimization methods cannot be applied to fuzzy rules learning. α-FUZZI-ES learning makes it possible to optimize fuzzy rules independently of each other. This property reduces the dimensionality of the search space in finding the optimum fuzzy rules. Thereby, α-FUZZI-ES learning can attain fast convergence in fuzzy rules optimization. Moreover, α-FUZZI-ES learning can be efficiently performed with hardware in parallel to optimize fuzzy rules independently of each other. Numerical results show that α-FUZZI-ES learning is superior to the exemplary conventional scheme in terms of accuracy and convergence speed when the evaluation function is non-differentiable.
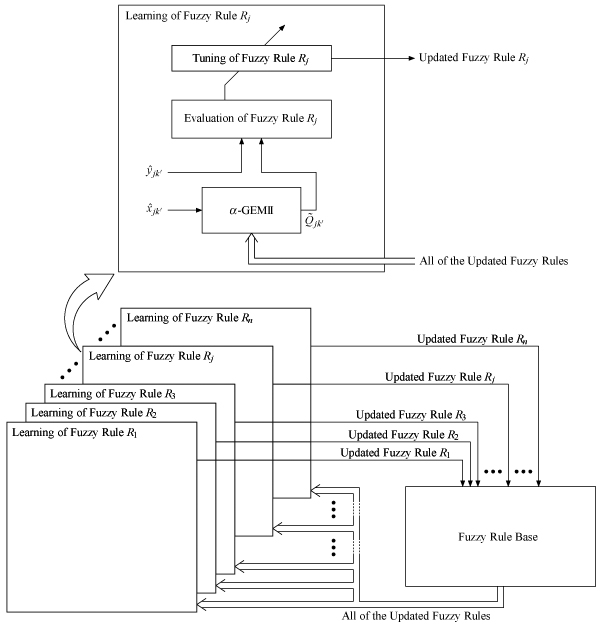
Parallel fuzzy rules optimization
- [1] L. N. de Castro and F. J. Von Zuben, “Learning and optimization using the clonal selection principle,” IEEE Trans. Evol. Comput., Vol.6, No.3, pp. 239-251, 2002.
- [2] K. M. Woldemariam and G. G. Yen, “Vaccine-enhanced artificial immune system for multimodal function optimization,” IEEE Trans. Syst., Man, Cybern., Part B: Cybernetics, Vol.40, No.1, pp. 218-228, 2010.
- [3] C.-H. Chen, C.-J. Lin, and C.-T. Lin, “Using an efficient immune symbiotic evolution learning for compensatory neuro-fuzzy controller,” IEEE Trans. Fuzzy Syst., Vol.17, No.3, pp. 668-682, 2009.
- [4] A. Chatterjee, K. Pulasinghe, K. Watanabe, and K. Izumi, “A particle-swarm-optimized fuzzy-neural network for voice-controlled robot systems,” IEEE Trans. Ind. Electron., Vol.52, No.6, pp. 1478-1489, 2005.
- [5] A. Chatterjee and K. Watanabe, “An optimized Takagi-Sugeno type neuro-fuzzy system for modeling robot manipulators,” Neural Comput. & Applic., Vol.15, No.1, pp. 55-61, 2006.
- [6] R. P. Prado, S. García-Galán, J. E. Muñoz Expósito, and A. J. Yuste, “Knowledge acquisition in fuzzy-rule-based systems with particle-swarm optimization,” IEEE Tran. Fuzzy Syst., Vol.18, No.6, pp. 1083-1097, 2010.
- [7] D. Chen, J. Wang, F. Zou, H. Zhang, and W. Hou, “Linguistic fuzzy model identification based on PSO with different length of particles,” Appl. Soft Comput., Vol.12, Issue 11, pp. 3390-3400, 2012.
- [8] K. Uehara and K. Hirota, “Independent evaluations of each fuzzy rule for derivative-free optimization of fuzzy systems: A feasibility study toward fast fuzzy-rule learning,” Proc. of the 6th Int. Workshop on Advanced Computational Intelligence and Intelligent Informatics (IWACIII2019), SUN4-C1, pp. 1-8, 2019.
- [9] K. Uehara, T. Koyama, and K. Hirota, “Fuzzy inference with schemes for guaranteeing convexity and symmetricity in consequences based on α-cuts,” J. Adv. Comput. Intell. Intell. Inform., Vol.13, No.2, pp. 135-149, 2009.
- [10] K. Uehara, T. Koyama, and K. Hirota, “Inference with governing schemes for propagation of fuzzy convex constraints based on α-cuts,” J. Adv. Comput. Intell. Intell. Inform., Vol.13, No.3, pp. 321-330, 2009.
- [11] K. Uehara and K. Hirota, “Noise reduction with inference based on fuzzy rule interpolation at an infinite number of activating points: Toward fuzzy rule learning in a unified inference platform,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.6, pp. 883-899, 2018.
- [12] K. Uehara and K. Hirota, “Fuzzy inference based on α-cuts and generalized mean: Relations between the methods in its family and their unified platform,” J. Adv. Comput. Intell. Intell. Inform., Vol.21, No.4, pp. 597-615, 2017.
- [13] K. Uehara and K. Hirota, “Multi-level control of fuzzy-constraint propagation in inference based on α-cuts and generalized mean,” J. Adv. Comput. Intell. Intell. Inform., Vol.17, No.4, pp. 647-662, 2013.
- [14] A. Khosravi, S. Nahavandi, and D. Creighton, “Prediction interval construction and optimization for adaptive neurofuzzy inference systems,” IEEE Trans. Fuzzy Syst., Vol.19, No.5, pp. 983-988, 2011.
- [15] C.-T. Lin, M. Prasad, and A. Saxena, “An improved polynomial neural network classifier using real-coded genetic algorithm,” IEEE Trans. Syst., Man, Cybern. Syst., Vol.45, No.11, pp. 1389-1401, 2015.
- [16] K. Mistry, L. Zhang, S. C. Neoh, C. P. Lim, and B. Fielding, “A micro-GA embedded PSO feature selection approach to intelligent facial emotion recognition,” IEEE Trans. Cybern., Vol.47, No.6, pp. 1496-1509, 2017.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.