Paper:
Characteristics of Rough Set C-Means Clustering
Seiki Ubukata, Keisuke Umado, Akira Notsu, and Katsuhiro Honda
Osaka Prefecture University
1-1 Gakuen-cho, Nakaku, Sakai, Osaka 599-8531, Japan
Hard C-means (HCM), which is one of the most popular clustering techniques, has been extended by using soft computing approaches such as fuzzy theory and rough set theory. Fuzzy C-means (FCM) and rough C-means (RCM) are respectively fuzzy and rough set extensions of HCM. RCM can detect the positive and the possible regions of clusters by using the lower and the upper areas which are respectively analogous to the lower and the upper approximations in rough set theory. RCM-type methods have the problem that the original definitions of the lower and the upper approximations are not actually used. In this paper, rough set C-means (RSCM), which is an extension of HCM based on the original rough set definition, is proposed as a rough set-based counterpart of RCM. Specifically, RSCM is proposed as a clustering model on an approximation space considering a space granulated by a binary relation and uses the lower and the upper approximations of temporal clusters. For this study, we investigated the characteristics of the proposed RSCM through basic considerations, visual demonstrations, and comparative experiments. We observed the geometric characteristics of the examined methods by using visualizations and numerical experiments conducted for the problem of classifying patients as having benign or malignant disease based on a medical dataset. We compared the classification performance by viewing the trade-off between the classification accuracy in the positive region and the fraction of objects classified as being in the positive region.
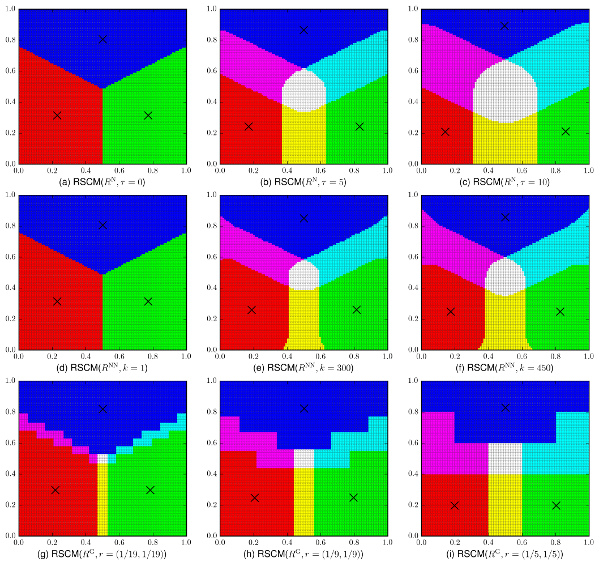
Clustering results by the proposed method for three different types of binary relations in the grid-point dataset.
- [1] J. B. MacQueen, “Some Methods of Classification and Analysis of Multivariate Observations,” Proc. 5th Berkeley Symp. Math. Stat. Prob., pp. 281-297, 1967.
- [2] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, 1981.
- [3] J. C. Dunn, “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters,” J. of Cybernetics, Vol.3, pp. 32-57, 1974.
- [4] R. N. Davé, “Characterization and Detection of Noise in Clustering,” Pattern Recognition Letters, Vol.12, No.11, pp. 657-664, 1991.
- [5] R. N. Davé and R. Krishnapuram, “Robust Clustering Methods: A Unified View,” IEEE Trans. on Fuzzy Systems, Vol.5, pp. 270-293, 1997.
- [6] Z. Pawlak, “Rough sets,” Int. J. of Computer & Information Sciences, Vol.11, Issue 5, pp. 341-356, 1982.
- [7] Z. Pawlak, “Rough Classification,” Int. J. of Man-Machine Studies, Vol.20, Issue 5, pp. 469-483, 1984.
- [8] Z. Pawlak, “Rough Set Approach to Knowledge-Based Decision Support,” European J. of Operational Research, Vol.99, Issue 1, pp. 48-57, 1997.
- [9] P. Lingras and C. West, “Interval Set Clustering of Web Users with Rough K-Means,” J. of Intelligent Information Systems, Vol.23, Issue 1, pp. 5-16, 2004.
- [10] G. Peters, “Some Refinements of Rough k-Means Clustering,” Pattern Recognition, Vol.39, Issue 8, pp. 1481-1491, 2006.
- [11] S. Ubukata, A. Notsu, and K. Honda, “General Formulation of Rough C-Means Clustering,” Int. J. of Computer Science and Network Security, Vol.17, No.9, pp. 1-10, 2017.
- [12] S. Mitra, H. Banka, and W. Pedrycz, “Rough-Fuzzy Collaborative Clustering,” IEEE Trans. on Systems, Man, and Cybernetics, Part B (Cybernetics), Vol.36, Issue 4, pp. 795-805, 2006.
- [13] S. Mitra and B. Barman, “Rough-Fuzzy Clustering: An Application to Medical Imagery,” Rough Sets and Knowledge Technology, Vol.5009 of the series Lecture Notes in Computer Science, pp. 300-307, 2008.
- [14] P. Maji and S. K. Pal, “RFCM: A Hybrid Clustering Algorithm Using Rough and Fuzzy Sets,” Fundamenta Informaticae, Vol.80, No.4, pp. 475-496, 2007.
- [15] Y. Endo and N. Kinoshita, “Various Types of Objective-Based Rough Clustering,” Fuzzy Sets, Rough Sets, Multisets and Clustering, Vol.671 of the series Studies in Computational Intelligence, pp. 63-85, 2017.
- [16] S. Ubukata, A. Notsu, and K. Honda, “The Rough Set k-Means Clustering,” Proc. of Joint 8th Int. Conf. on Soft Computing and Intelligent Systems and 17th Int. Symp. on Advanced Intelligent Systems, pp. 189-193, 2016.
- [17] Y. Y. Yao, “Generalized rough set models,” Rough Sets in Knowledge Discovery, Physica-Verlag, pp. 286-318, 1998.
- [18] Z. Pawlak and A. Skowron, “Rough Membership Function: A Tool for Reasoning with Uncertainty,” Algebraic Methods in Logic and Computer Science, Banach Center Publications, Vol.28, pp. 135-150, 1993.
- [19] Z. Pawlak and A. Skowron, “Rough membership functions,” Advances in the Dempster-Shafer Theory of Evidence, Wiley, pp. 251-271, 1994.
- [20] Q. Hu, D. Yu, and Z. Xie, “Neighborhood Classifiers,” Expert Systems with Applications, Vol.34, Issue 2, pp. 866-876, 2008.
- [21] Q. Hu et al., “Neighborhood Rough Set Based Heterogeneous Feature Subset Selection,” Information Sciences, Vol.178, Issue 18, pp. 3577-3594, 2008.
- [22] I. Bloch, “On Links Between Mathematical Morphology and Rough Sets,” Pattern Recognition, Vol.33, Issue 9, pp. 1487-1496, 2000.
- [23] UCI Machine Learning Repository, http://archive.ics.uci.edu/ml/ [accessed March 5, 2018]
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.