Paper:
Maximum-Margin Model for Nearest Prototype Classifiers
Yoshifumi Kusunoki, Chiharu Wakou, and Keiji Tatsumi
Graduate School of Engineering, Osaka University
2-1 Yamada-oka, Suita, Osaka 565-0871, Japan
In this paper, we study nearest prototype classifiers, which classify data instances into the classes to which their nearest prototypes belong. We propose a maximum-margin model for nearest prototype classifiers. To provide the margin, we define a class-wise discriminant function for instances by the negatives of distances of their nearest prototypes of the class. Then, we define the margin by the minimum of differences between the discriminant function values of instances with respect to the classes they belong to and the values of the other classes. The optimization problem corresponding to the maximum-margin model is a difference of convex functions (DC) program. It is solved using a DC algorithm, which is a k-means-like algorithm, i.e., the members and positions of prototypes are alternately optimized. Through a numerical study, we analyze the effects of hyperparameters of the maximum-margin model, especially considering the classification performance.
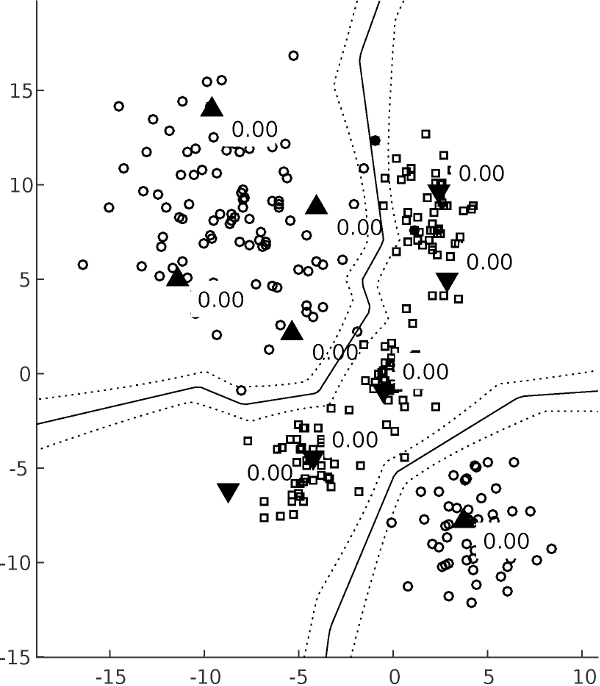
Separation by prototypes
- [1] S.-W. Kim and B. J. Oommen, “A brief taxonomy and ranking of creative prototype reduction schemes,” Pattern Analysis & Applications, Vol.6, No.3, pp. 232-244, 2003.
- [2] I. Triguero, J. Derrac, S. Garcia, and F. Herrera, “A Taxonomy and Experimental Study on Prototype Generation for Nearest Neighbor Classification,” IEEE Trans. on Systems, Man, and Cybernetics, Vol.42, No.1, pp. 86-100, 2012.
- [3] N. Lavrač, B. Kavšek, P. Flach, and L. Todorovski, “Subgroup Discovery with CN2-SD,” J. Mach. Learn. Res., Vol.5, pp. 153-188, 2004.
- [4] V. N. Vapnik, “Statistical Learning Theory,” A Wiley-Interscience Publication, 1998.
- [5] S. Abe, ”Support Vector Machines for Pattern Classification,” 2nd edition, Springer-Verlag London, 2010.
- [6] P. D. Tao and H. A. L. Thi, “Convex analysis approach to d.c. programming: Theory, Algorithm and Applications,” Vol.22, pp. 289-355, 1997.
- [7] L. T. H. An and P. D. Tao, “The DC (Difference of Convex Functions) Programming and DCA Revisited with DC Models of Real World Nonconvex Optimization Problems,” Annals of Operations Research, Vol.133, No.1, pp. 23-46, 2005.
- [8] J. C. Bezdek and L. I. Kuncheva, “Nearest prototype classifier designs: An experimental study,” Int. J. of Intelligent Systems, Vol.16, No.12, pp. 1445-1473, 2001.
- [9] C.-L. Chang, “Finding Prototypes For Nearest Neighbor Classifiers,” IEEE Trans. on Computers, Vol.C-23, Issue 11, pp. 1179-1184, 1974.
- [10] J. C. Bezdek, T. R. Reichherzer, G. S. Lim, and Y. Attikiouzel, “Multiple-prototype classifier design,” IEEE Trans. on Systems, Man, and Cybernetics, Part C (Applications and Reviews), Vol.28, No.1, pp. 67-79, 1998.
- [11] T. Kohonen, “The self-organizing map,” Proc. of the IEEE, Vol.78, No.9, pp. 1464-1480, 1990.
- [12] R. Odorico, “Learning Vector Quantization with Training Count (LVQTC),” Neural Networks, Vol.10, No.6, pp. 1083-1088, 1997.
- [13] A. Cervantes, I. M. Galvan, and P. Isasi, “AMPSO: A New Particle Swarm Method for Nearest Neighborhood Classification,” IEEE Trans. on Systems, Man, and Cybernetics, Part B (Cybernetics), Vol.39, No.5, pp. 1082-1091, 2009.
- [14] I. Triguero, S. Garca, and F. Herrera, “Differential evolution for optimizing the positioning of prototypes in nearest neighbor classification,” Pattern Recognition, Vol.44, No.4, pp. 901-916, 2011.
- [15] H. Ichihashi, K. Nagaura, A. Notsu, and K. Honda, “Benchmarking Parameterized Fuzzy c-Means Classifier,” J. of Japan Society for Fuzzy Theory and Intelligent Informatics, Vol.22, No.5, pp. 609-620, 2010 (in Japanese).
- [16] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering: Methods in c-Means Clustering with Applications,” Springer, 2008.
- [17] M. Lozano et al., “Experimental study on prototype optimisation algorithms for prototype-based classification in vector spaces,” Pattern Recognition, Vol.39, No.10, pp. 1827-1838, 2006.
- [18] M. Mohri, A. Rostamizadeh, and A. Talwalkar, “Foundations of Machine Learning,” The MIT Press, 2012.
- [19] H. Tuy, “Convex Analysis and Global Optimization,” Springer International Publishing, 2016.
- [20] L. T. H. An, M. T. Belghiti, and P. D. Tao, “A new efficient algorithm based on DC programming and DCA for clustering,” J. Glob. Optim., Vol.38, pp. 593-608, 2007.
- [21] M. ApS, “The MOSEK optimization toolbox for MATLAB manual. Version 8.1.,” 2015.
- [22] V. Jeyakumar and D. T. Luc, “Nonsmooth Vector Functions and Continuous Optimization,” Springer US, 2008.
- [23] D. Arthur and S. Vassilvitskii, “K-means++: The Advantages of Careful Seeding,” Proc. of the Eighteenth Annual ACM-SIAM Symp. on Discrete Algorithms, SODA ’07, pp. 1027-1035, 2007.
- [24] W. Lam, C.-K. Keung, and D. Liu, “Discovering useful concept prototypes for classification based on filtering and abstraction,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.24, No.8, pp. 1075-1090, 2002.
- [25] R. H. Tütüncü, K. C. Toh, and M. J. Todd, “Solving semidefinite-quadratic-linear programs using SDPT3,” Mathematical Programming, Vol.95, No.2, pp. 189-217, 2003.
- [26] I. Pólik and T. Terlaky, “Interior Point Methods for Nonlinear Optimization,” Nonlinear Optimization, pp. 215-276, Springer Berlin Heidelberg, 2010.
- [27] D. Dheeru and E. Karra Taniskidou, “UCI Machine Learning Repository,” 2017.
- [28] J. Weston and C. Watkins, “Support vector machines for multi-class pattern recognition,” In ESANN, pp. 219-224, 1999.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.