Paper:
Cluster Validity Measures for Network Data
Yukihiro Hamasuna*1, Daiki Kobayashi*2, Ryo Ozaki*3, and Yasunori Endo*4
*1Department of Informatics, School of Science and Engineering, Kindai University
3-4-1 Kowakae, Higashiosaka, Osaka 577-8502, Japan
*2Graduate School of Science and Engineering, Kindai University
3-4-1 Kowakae, Higashiosaka, Osaka 577-8502, Japan
*3ALBERT Inc.
1-26-2 Nishishinjuku, Shinjuku-ku, Tokyo 163-0515, Japan
*4Faculty of Engineering, Information and Systems, University of Tsukuba
1-1-1 Tennodai, Tsukuba, Ibaraki 305-8573, Japan
Modularity is one of the evaluation measures for network partitions and is used as the merging criterion in the Louvain method. To construct useful cluster validity measures and clustering methods for network data, network cluster validity measures are proposed based on the traditional indices. The effectiveness of the proposed measures are compared and applied to determine the optimal number of clusters. The network cluster partitions of various network data which are generated from the Polaris dataset are obtained by k-medoids with Dijkstra’s algorithm and evaluated by the proposed measures as well as the modularity. Our numerical experiments show that the Dunn’s index and the Xie-Beni’s index-based measures are effective for network partitions compared to other indices.
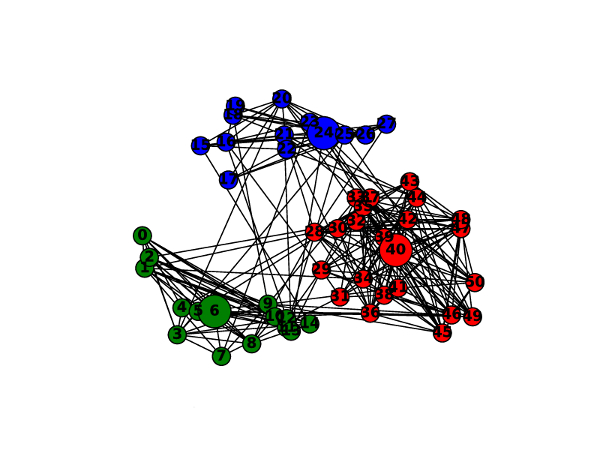
An illustrative example of the network data used in experiments.
- [1] M. Newman, “Networks: An Introduction,” Oxford University Press, 2010.
- [2] M. E. J. Newman, “Modularity and community structure in networks,” PNAS, Vol.103, No.23, pp. 8577-8582, 2006.
- [3] V. D. Blondel et al., “Fast unfolding of communities in large networks,” J. of Statistical Mechanics: Theory and Experiment, p. P10008, 2008.
- [4] J. C. Dunn, “Well separated clusters and optimal fuzzy partitions,” J. of Cybernetics, Vol.4, pp. 95-104, 1974.
- [5] I. Gath and A. B. Geva, “Unsupervised optimal fuzzy clustering,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.11, No.7, pp. 773-780, 1989.
- [6] X. L. Xie and G. Beni, “A validity measure for fuzzy clustering,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.13, No.8, pp. 841-847, 1991.
- [7] W. Wang and Y. Zhang, “On fuzzy cluster validity indices,” Fuzzy Sets and Systems, Vol.158, No.19, pp. 2095-2117, 2007.
- [8] S. Miyamoto, H. Ichihashi, and K. Honda, “Algorithms for Fuzzy Clustering,” Springer, 2008.
- [9] W. Hashimoto, T. Nakamura, and S. Miyamoto, “Comparison and evaluation of different cluster validity measures including their kernelization,” J. Adv. Comput. Intell. Intell. Inform., Vol.13, No.3, pp. 204-209, 2009.
- [10] I. J. Sledge et al., “Relational Generalizations of Cluster Validity Indices,” IEEE Trans. on Fuzzy Systems, Vol.18, No.4, pp. 771-786, 2010.
- [11] Y. Hamasuna, R. Ozaki, and Y. Endo, “A study on cluster validity measures for clustering network data,” Joint 17th World Congress of lnt. Fuzzy Systems Association and 9th Int. Conf. on Soft Computing and Intelligent Systems (IFSA-SCIS2017), #89, 2017.
- [12] L. Kaufman and P. J. Rousseeuw, “Finding Groups in Data: An Introduction to Cluster Analysis,” Wiley, 1990.
- [13] A. K. Jain, “Data clustering: 50 years beyond K-means,” Pattern Recognition Letters, Vol.31, No.8, pp. 651-666, 2010.
- [14] J. C. Bezdek, “Pattern Recognition with Fuzzy Objective Function Algorithms,” Plenum Press, 1981.
- [15] R. I. Kondor and J. Lafferty, “Diffusion kernels on graphs and other discrete structures,” Proc. of the 19th Int. Conf. on Machine Learning (ICML’02), pp. 315-322, 2002.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.