Paper:
CFD Analysis of Takeoff from a Water Surface for an Insect-Scale Aerial/Aquatic Robot
Noa Hashimoto, Rui Suzuki, and Koki Kikuchi

Department of Advanced Robotics, Faculty of Advanced Engineering, Chiba Institute of Technology
2-17-1 Tsudanuma, Narashino, Chiba 275-0016, Japan
To develop an insect-scale aerial/aquatic robot, we analyzed takeoff mechanisms to counteract surface tension, such as paddling, slapping, and clap-and-fling. Because a diving beetle, Eretes griseus, takes off directly from the water surface, a flapping-wing robot is promising as an alternative to a drone with multiple rotary wings. In this study, we first investigated diving beetle flight with a three-dimensional high-speed camera system and analyzed the motion characteristics. Subsequently, we developed a computational fluid dynamics method that tracked the water surface using a volume of fluid method, reproduced the motion with a multibody model, treated the deformation of the elastic membrane wing with the phase delay of the joint angle functions, and simulated takeoff, that is, the transition from water to air, and hovering near the water surface. The simulation result showed that during the transition, the slapping motion exerted the maximum and average lift per unit of body weight of 18 and 9.2, respectively, while those of paddling produced 0.46 and 0.23, respectively. The water surface effect improved the lift by 25% at the normalized height of less than 0.44 and disappeared at a height greater than 0.7. During hovering, while the clap-and-fling motion improved lift by 2.6% and the water surface effect was 9.8%, the synergy effect was 22%. In addition, the former enhanced it significantly after the fling, while the latter was remarkable during the wing acceleration phase. In contrast to ground effects, flapping reduced the water level and caused the ripples, dynamically changing the water surface effect.
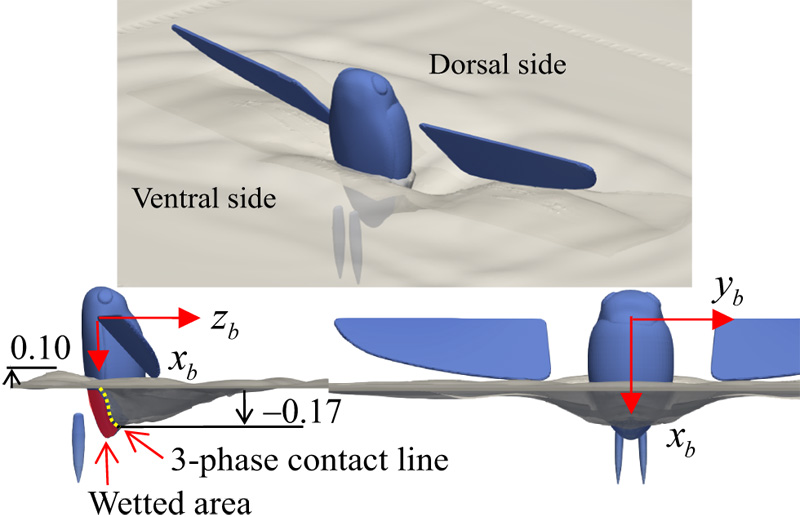
Water surface state at 33 ms
- [1] H. Tanaka, T. Nakata, and T. Yamasaki, “Biomimetic soft wings for soft robot science,” J. Robot. Mechatron., Vol.34, No.2, pp. 223-226, 2022. https://doi.org/10.20965/jrm.2022.p0223
- [2] M. M. Maia, P. Soni, and F. J. Diez, “Demonstration of an aerial and submersible vehicle of flight and underwater navigation with seamless air-water transition,” arXiv:1507.01932, 2015. https://doi.org/10.48550/arXiv.1507.01932
- [3] Y. Chen et al., “A biologically inspired, flapping-wing, hybrid aerial-aquatic microrobot,” Science Robotics, Vol.2, No.11, Article No.eaao5619, 2017. https://doi.org/10.1126/scirobotics.aao5619
- [4] J. A. Nirody et al., “Geckos race across the water’s surface using multiple mechanisms,” Current Biology, Vol.28, No.24, pp. 4046-4051, 2018. https://doi.org/10.1016/j.cub.2018.10.064
- [5] T. Weis-Fogh, “Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production,” J. of Experimental Biology, Vol.59, No.1, pp. 169-230, 1973. https://doi.org/10.1242/jeb.59.1.169
- [6] H. V. Phan, T. K. L. Au, and H. C. Park, “Clap-and-fling mechanism in a hovering insect-like two-winged flapping-wing micro air vehicle,” Royal Society Open Science, Vol.3, No.12, Article No.160746, 2016. https://doi.org/10.1098/rsos.160746
- [7] R. Siddall and M. Kovac, “Fast aquatic escape with a jet thruster,” IEEE/ASME Trans. on Mechatronics, Vol.22, No.1, pp. 217-226, 2017. https://doi.org/10.1109/TMECH.2016.2623278
- [8] Y. Tanabe, H. Sugawara, S. Sunada, K. Yonezawa, and H. Tokutake, “Quadrotor drone hovering in ground effect,” J. Robot. Mechatron., Vol.33, No.2, pp. 339-347, 2021. https://doi.org/10.20965/jrm.2021.p0339
- [9] T. V. Truong, D. Byun, M. J. Kim, K. J. Yoon, and H. C. Park, “Aerodynamic forces and flow structures of the leading edge vortex on a flapping wing considering ground effect,” Bioinspiration & Biomimetics, Vol.8, No.3, Article No.036007, 2013. https://doi.org/10.1088/1748-3182/8/3/036007
- [10] H. Mukundarajan, T. C. Bardon, D. H. Kim, and M. Prakash, “Surface tension dominates insect flight on fluid interfaces,” J. of Experimental Biology, Vol.219, No.5, pp. 752-766, 2016. https://doi.org/10.1242/jeb.127829
- [11] P. E. Sitorus, H. C. Park, D. Byun, N. S. Goo, and C. H. Han, “The role of elytra in beetle flight: I. Generation of quasi-static aerodynamic forces,” J. of Bionic Engineering Vol.7, No.4, pp. 354-363, 2010. https://doi.org/10.1016/S1672-6529(10)60267-3
- [12] M. Shindo, T. Fujikawa, and K. Kikuchi, “Analysis of roll rotation mechanism of a butterfly for development of a small flapping robot,” American Trans. on Engineering & Applied Sciences, Vol.3, No.4, pp. 233-250, 2014.
- [13] Y. Ozawa, T. Fujikawa, and K. Kikuchi, “Analysis of turning motion for developing a butterfly-style flapping robot,” MM Science J., Vol.2018, No.3, pp. 2198-2204, 2018. https://doi.org/10.17973/MMSJ.2018_03_201765
- [14] K. Sanuki and T. Fujikawa, “Motion analysis of butterfly-style flapping robot using CFD based on 3D-CAD model and experimental flight data,” J. Robot. Mechatron., Vol.33, No.2, pp. 216-222, 2021. https://doi.org/10.20965/jrm.2021.p0216
- [15] L. A. Miller and C. S. Peskin, “Flexible clap and fling in tiny insect flight,” J. of Experimental Biology, Vol.212, No.19, pp. 3076-3090, 2009. https://doi.org/10.1242/jeb.028662
- [16] A. Santhanakrishnan et al., “Clap and fling mechanism with interacting porous wings in tiny insect flight,” J. of Experimental Biology, Vol.217, No.21, pp. 3898-3909, 2014. https://doi.org/10.1242/jeb.084897
- [17] H. K. Versteeg and W. Malalasekera, “An Introduction to Computational Fluid Dynamics: The Finite Volume Method,” 2nd Edition, Prentice Hall, 2007.
- [18] C. W. Hirt and B. D. Nichols, “Volume of fluid (VOF) method for the dynamics of free boundaries,” J. of Computational Physics, Vol.39, No.1, pp. 201-225, 1981. https://doi.org/10.1016/0021-9991(81)90145-5
- [19] W. Meng, C. Yu, J. Li, and R. An, “Numerical simulation of gas-liquid two-phase flow impacting fixed structure by CLSVOF/IB method based on OpenFOAM,” J. of Hydrodynamics, Vol.33, No.6, pp. 1176-1189, 2021. https://doi.org/10.1007/s42241-021-0100-2
- [20] A. Q. Raeini, M. J. Blunt, and B. Bijeljic, “Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method,” J. of Computational Physics, Vol.231, No.17, pp. 5653-5668, 2012. https://doi.org/10.1016/j.jcp.2012.04.011
- [21] K. Ahmed, A. A. Hamada, L. Chatellier, and M. Furth, “A modified overset method in OpenFOAM for simultaneous motion and deformation: A case study of a flexible flapping foil,” OpenFOAM® J., Vol.4, pp. 41-61, 2024. https://doi.org/10.51560/ofj.v4.96
- [22] C. Liu, J. Ju, Y. Zheng, and L. Jiang, “Asymmetric ratchet effect for directional transport of fog drops on static and dynamic butterfly wings,” ACS Nano, Vol.8, No.2, pp. 1321-1329, 2014. https://doi.org/10.1021/nn404761q
- [23] D. Qi et al., “Observation and analysis of diving beetle movement while swimming,” Scientific Reports, Vol.11, Article No.16581, 2021. https://doi.org/10.1038/s41598-021-96158-1
- [24] S. Sudo, T. Yano, Y. Kan, Y. Yamada, and K. Tsuyuki, “Swimming behavior of small diving beetles,” J. of Advanced Science, Vol.18, Nos.1+2, pp. 46-49, 2006. https://doi.org/10.2978/jsas.18.46
- [25] J. W. Glasheen and T. A. Mcmahon, “Size-dependence of water-running ability in basilisk lizards (Basiliscus basiliscus),” J. of Experimental Biology, Vol.199, No.12, pp. 2611-2618, 1996. https://doi.org/10.1242/jeb.199.12.2611
- [26] L. T. K. Au, H. C. Park, S. T. Lee, and S. K. Hong, “Clap-and-fling mechanism in non-zero inflow of a tailless two-winged flapping-wing micro air vehicle,” Aerospace, Vol.9, No.2, Article No.108, 2016. https://doi.org/10.3390/aerospace9020108
- [27] M. H. Dickinson, F.-O. Lehmann, and S. P. Sane, “Wing rotation and the aerodynamic basis of insect flight,” Science, Vol.284, No.5422, pp. 1954-1960, 1999. https://doi.org/10.1126/science.284.5422.1954
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.