Paper:
Quad-Rotor Avoidance Trajectory Generation for Convex Polyhedron Obstacles
Yoshihide Arai, Takashi Sago, Yuki Ueyama, and Masanori Harada
National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
This study investigates a method for generating obstacle avoidance trajectories for arbitrary convex polyhedrons. We propose a formulation that converts discrete conditions into continuous equation forms to avoid convex polyhedron obstacles. The condition that the evaluation point be located outside of the convex polyhedron can be transformed into a constraint in the continuous equation form and incorporated into the optimization calculation to generate avoidance trajectories. Avoidance trajectory generation using the Legendre pseudospectral method is performed for convex polyhedral obstacles of various shapes. The results show that the proposed method successfully generates avoidance trajectories for arbitrary convex polyhedral obstacles.
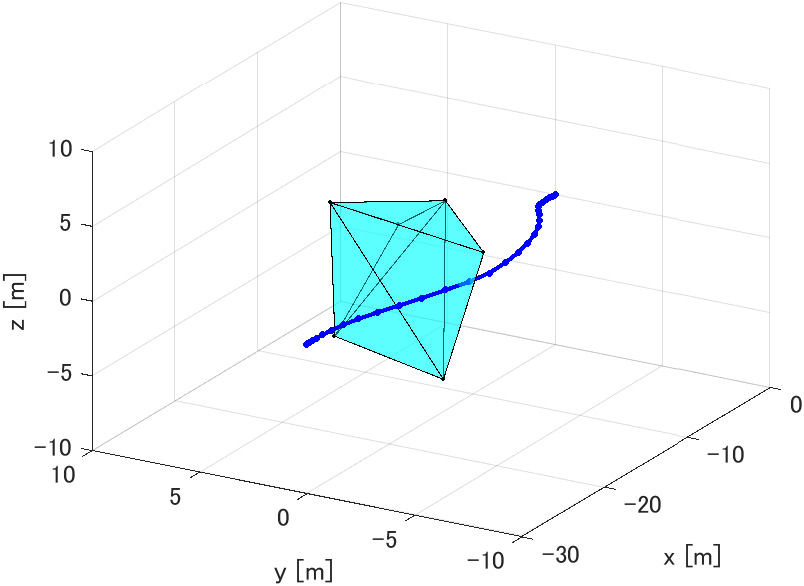
Convex polyhedron obstacle avoidance
- [1] L. R. Lewis, I. M. Ross, and Q. Gong, “Pseudospectral motion planning techniques for autonomous obstacle avoidance,” 46th IEEE Conf. on Decision and Control, pp. 5997-6002, 2007. https://doi.org/10.1109/CDC.2007.4434545
- [2] Q. Gong, L. R. Lewis, and I. M. Ross, “Pseudospectral motion planning for autonomous vehicles,” J. of Guidance, Control, and Dynamics, Vol.32, No.3, pp. 1039-1045, 2009. https://doi.org/10.2514/1.39697
- [3] Y. Suzuki, S. Thompson, and S. Kagami, “Smooth path planning with pedestrian avoidance for wheeled robots,” J. Robot. Mechatron., Vol.22, No.1, pp. 21-27, 2010. https://doi.org/10.20965/jrm.2010.p0021
- [4] R. B. Patel and P. J. Goulart, “Trajectory generation for aircraft avoidance maneuvers using online optimization,” J. of Guidance, Control, and Dynamics, Vol.34, No.1, pp. 218-230, 2011. https://doi.org/10.2514/1.49518
- [5] Y. Kobayashi, M. Kondo, Y. Hiramatsu, H. Fujii, and T. Kamiya, “Mobile robot decision-making based on offline simulation for navigation over uneven terrain,” J. Robot. Mechatron., Vol.30, No.4, pp. 671-682, 2018. https://doi.org/10.20965/jrm.2018.p0671
- [6] R. Bonalli, A. Cauligi, A. Bylard, and M. Pavone, “GuSTO: Guaranteed sequential trajectory optimization via sequential convex programming,” 2019 Int. Conf. on Robotics and Automation (ICRA), pp. 6741-6747, 2019. https://doi.org/10.1109/ICRA.2019.8794205
- [7] M. Szmuk, D. Malyuta, T. P. Reynolds, M. S. Mceowen, and B. Açikmeşe, “Real-time quad-rotor path planning using convex optimization and compound state-triggered constraints,” arXiv:1902.09149, 2019. https://doi.org/10.48550/arXiv.1902.09149
- [8] H. Taghavifar, B. Xu, L. Taghavifar, and Y. Qin, “Optimal path-planning of nonholonomic terrain robots for dynamic obstacle avoidance using single-time velocity estimator and reinforcement learning approach,” IEEE Access, Vol.7, pp. 159347-159356, 2019. https://doi.org/10.1109/ACCESS.2019.2950166
- [9] E. Aldao, L. M. González-deSantos, H. Michinel, and H. González-Jorge, “UAV obstacle avoidance algorithm to navigate in dynamic building environments,” Drones, Vol.6, No.1, Article No.16, 2022. https://doi.org/10.3390/drones6010016
- [10] D. Malyuta et al., “Convex optimization for trajectory generation: A tutorial on generating dynamically feasible trajectories reliably and efficiently,” IEEE Control Systems Magazine, Vol.42, No.5, pp. 40-113, 2022. https://doi.org/10.1109/MCS.2022.3187542
- [11] K. Tracy, T. A. Howell, and Z. Manchester, “Differentiable collision detection for a set of convex primitives,” 2023 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3663-3670, 2023. https://doi.org/10.1109/ICRA48891.2023.10160716
- [12] Y. Arai, T. Sago, Y. Ueyama, and M. Harada, “MGV obstacle avoidance trajectory generation considering vehicle shape,” J. Robot. Mechatron., Vol.35, No.2, pp. 262-270, 2023. https://doi.org/10.20965/jrm.2023.p0262
- [13] Y. Arai, T. Sago, Y. Ueyama, and M. Harada, “Avoidance trajectory generation for quad-rotors by polygonal bounding of congested obstacles,” AIAA SCITECH 2024 Forum, 2024. https://doi.org/10.2514/6.2024-1596
- [14] M. Karpenko, P. Sekhavat, J. Park, and I. Ross, “Closed-loop optimal guidance and control of quadrotor unmanned aerial vehicle,” AIAA Guidance, Navigation, and Control Conf., 2010. https://doi.org/10.2514/6.2010-8051
- [15] H. Kawano, “Three-dimensional obstacle avoidance of blimp-type unmanned aerial vehicle flying in unknown and non-uniform wind disturbance,” J. Robot. Mechatron., Vol.19, No.2, pp. 166-173, 2007. https://doi.org/10.20965/jrm.2007.p0166
- [16] Y. Kobayashi and T. Nomura, “Learning of obstacle avoidance with redundant manipulator by hierarchical SOM,” J. Adv. Comput. Intell. Intell. Inform., Vol.15, No.5, pp. 525-531, 2011. https://doi.org/10.20965/jaciii.2011.p0525
- [17] A. E. Bryson, Jr. and Y.-C. Ho, “Applied Optimal Control,” Taylor & Francis, 1975. https://doi.org/10.1201/9781315137667
- [18] I. M. Ross, “A Primer on Pontryagin’s Principle in Optimal Control,” 2nd Edition, Collegiate Publishers, 2015.
- [19] F. Fahroo and I. M. Ross, “Costate estimation by a Legendre pseudospectral method,” J. of Guidance, Control, and Dynamics, Vol.24, No.2, pp. 270-277, 2001. https://doi.org/10.2514/2.4709
- [20] M. Harada, “Direct trajectory optimization by a Jacobi pseudospectral method with the weights of high-order Gauss-Lobatto formulae,” Trans. of the Japan Society of Mechanical Engineers, Ser. C, Vol.73, No.728, pp. 1075-1080, 2007 (in Japanese). https://doi.org/10.1299/kikaic.73.1075
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.