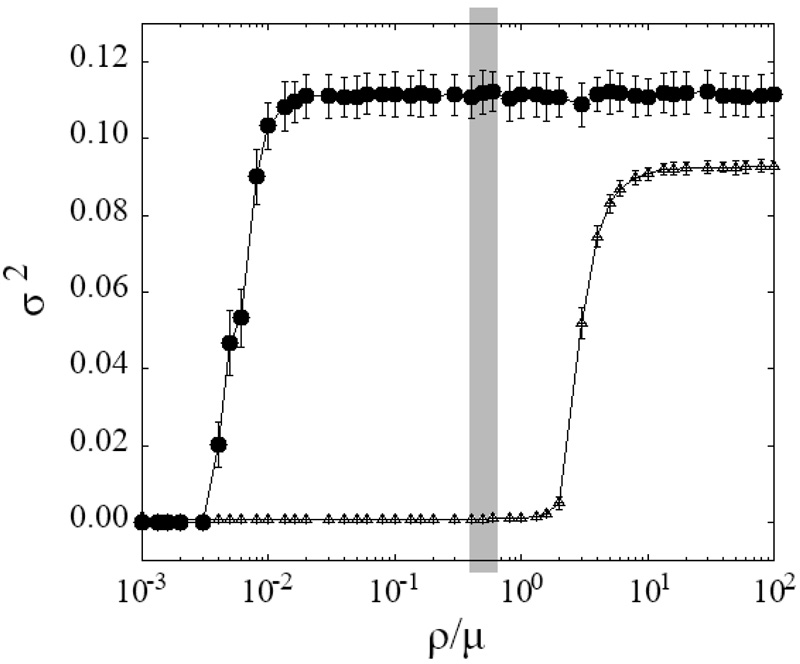
In the Bonabeau model, chemotaxis, which is observed in social insects, such as ants, was introduced into the movement rules of agents to control the collision frequency between agents, and its effect on the mechanism of hierarchical structure formation was investigated. Like an ant, this chemotactic agent makes stochastic decisions regarding its direction of movement depending on the intensity of its released chemicals. Because of this mechanism, the agent depends on its past location history. It can perform different motions from a random walk (RW) and asymmetric attractive or repulsive interactions with other agents via the diffusion of chemotactic substances. When there is an attractive interaction between these agents, they are more likely to aggregate, which increases the effective density; thus, the disparity in the agent winning ratio is more likely to form than in a conventional model with a RW. However, in the case of repulsive interactions, the agents became more distant from each other, the effective density decreased, and a disparity in the winning ratio was less likely to form. This indicates that the disparity in the winning ratio is tunable owing to the interactions between the introduced chemotactic agents.

1. [1] H. Murakami, M. Abe, and Y. Nishiyama, “Toward Comparative Collective Behavior to Discover Fundamental Mechanisms Underlying Behavior in Human Crowds and Nonhuman Animal Groups,” J. Robot. Mechatron., Vol.35, No.4, pp. 922-930, 2023. https://doi.org/10.20965/jrm.2023.p0922
2. [2] M. Hiraga and K. Ohkura, “Effects of Congestion on Swarm Performance and Autonomous Specialization in Robotic Swarms,” J. Robot. Mechatron., Vol.31, No.4, pp. 526-534, 2019. https://doi.org/10.20965/jrm.2019.p0526
3. [3] T. Kitazato, M. Hoshino, M. Ito, and K. Sezaki, “Detection of Pedestrian Flow Using Mobile Devices for Evacuation Guiding in Disaster,” J. Disaster Res., Vol.13, No.2, pp. 303-312, 2018. https://doi.org/10.20965/jdr.2018.p0303
4. [4] M. Jusup, P. Holme, K. Kanazawa, M. Takayasu, I. Romić, Z. Wang, S. Geček, T. Lipić, B. Podobnik, L. Wang, W. Luo, T. Klanjšček, J. Fan, S. Boccaletti, and M. Perc, “Social physics,” Physics Reports, Vol.948, pp. 1-148, 2022. https://doi.org/10.1016/j.physrep.2021.10.005
5. [5] C. Castellano, S. Ortunato, and V. Loreto, “Statistical physics of social dynamics,” Reviews of Modern Physics, Vol.81, Issue 2, Article No.591, 2009. https://doi.org/10.1103/RevModPhys.81.591
6. [6] E. Bonabeau, “Agent-based modeling: Methods and techniques for simulating human systems,” Proc. National Academy of Sciences, Vol.99, No.suppl_3, pp. 7280-7287, 2002. https://doi.org/10.1073/pnas.082080899
7. [7] E. Bonabeau, G. Theraulaz, and J.-L. Deneubourg, “Phase diagram of a model of self-organizing hierarchies,” Physica A, Vol.217, Issues 3-4, pp. 373-392, 1995. https://doi.org/10.1016/0378-4371(95)00064-E
8. [8] B. Hölldobler and E. O. Wilson, “The Ants,” Belknap Press, 1990.
9. [9] H. Zeng, “Functional properties of ant queen pheromones as revealed by behavioral experiments,” Behavioral Ecology and Sociobiology, Vol.77, Article No.113, 2023. https://doi.org/10.1007/s00265-023-03378-8
10. [10] M. F. Ali and E. D. Morgan, “Chemical Communication in Insect Communities: A Guide to Insect Pheromones with Special Emphasis on Social Insects,” Biol. Rev., Vol.65, Issue 3, pp. 227-247, 1990. https://doi.org/10.1111/j.1469-185X.1990.tb01425.x
11. [11] C. Burstedde, K. Klauck, A. Schadschneider, and J. Zittartz, “Simulation of pedestrian dynamics using a two-dimensional cellular automaton,” Physica A, Vol.295, Issues 3-4, pp. 507-525, 2001. https://doi.org/10.1016/S0378-4371(01)00141-8
12. [12] A. Kirchner, K. Nishinari, and A. Schadschneider, “Friction effects and clogging in a cellular automaton model for pedestrian dynamics,” Physical Review E, Vol.67, Issue 5, Article No.056122, 2003. https://doi.org/10.1103/PhysRevE.67.056122
13. [13] A.-L. Barabasi and R. Albert, “Emergence of scaling in random networks,” Science, Vol.286, Issue 5439, pp. 509-512, 1999. https://doi.org/10.1126/science.286.5439.509
14. [14] R. Albert and A.-L. Barabasi, “Statistical mechanics of complex networks,” Reviews of Modern Physics, Vol.74, Issue 1, Article No.47, 2002. https://doi.org/10.1103/RevModPhys.74.47
15. [15] T. Okubo and T. Odagaki, “Mean-field analysis of phase transitions in the emergence of hierarchical society,” Physical Review E, Vol.76, Issue 3, Article No.036105, 2007. https://doi.org/10.1103/PhysRevE.76.036105
16. [16] C. Oosawa, “A model of camphor-type self-driven particle,” Proc. of the 26th Symp. on Traffic Flow and Self-driven Particles, pp. 55-58, 2020.
17. [17] C. Oosawa, “Group Chase and Escape with Chemotaxis,” J. Robot. Mechatron., Vol.35, No.4, pp. 918-921, 2023. https://doi.org/10.20965/jrm.2023.p0918
18. [18] C. Oosawa, “Motility and stability of chemotactic agents that chained linearly,” Papers of the 29th Symp. on Traffic Flow and Self-driven Particles, pp. 17-20, 2023.
19. [19] C. Oosawa, “Dependence of Péclet Number on agent-based chemotactic predator-prey system,” Proc. of the 29th Int. Symp. on Artificial Life and Robotics 2024 (AROB 29th 2024), pp. 857-861, 2024.
20. [20] R. Fujie and T. Odagaki, “Self organization of social hierarchy and clusters in a challenging society with free random walks,” Physica A, Vol.389, Issue 7, pp. 1471-1479, 2010. https://doi.org/10.1016/j.physa.2009.11.042
21. [21] R. Fujie and T. Odagaki, “Self Organization of Social Hierarchy in Competitive Societies,” J. of Physical Society Japan, Vol.80, No.12, Article No.124802, 2011. https://journals.jps.jp/doi/pdf/10.1143/JPSJ.80.124802
22. [22] T. Odagaki and A. Ishifuku, “Self-Organization of Extreme Inequalities in a Competitive Society,” Acta Physica Polonica A, Vol.133, No.6, pp. 1459-1464, 2018. https://doi.org/10.12693/APhysPolA.133.1459
23. [23] G. G. Naumis, M. D. Castillo-Mussot, L. A. Pérez, and G. J. Vázquez, “Social Hierarchies with an Attractive Site Distribution,” Int. J. of Modern Physics C, Vol.17, No.03, pp. 403-408, 2006. https://doi.org/10.1142/S0129183106008546
24. [24] S. N. Dorogovtsev and J. F. F. Mendes, “Evolution of Networks,” Advances in Physics, Vol.51, Issue 4, pp. 1079-1187, 2002. https://doi.org/10.1080/00018730110112519
25. [25] T. Takemoto and C. Oosawa, “Introduction to Complex Networks: Measures, Statistical Properties, and Models,” M. Dehmer and S. C. Basak (Eds.), “Statistical and Machine Learning Approaches for Network Analysis,” pp. 45-75, John Wiley & Sons, Inc. 2012. https://doi.org/10.1002/9781118346990.ch2
26. [26] T. Takemoto and C. Oosawa, “Modeling for Evolving Biological Networks,” M. Dehmer and S. C. Basak (Eds.), “Statistical and Machine Learning Approaches for Network Analysis,” pp. 77-108, John Wiley & Sons, Inc., 2012. https://doi.org/10.1002/9781118346990.ch3
27. [27] K. Malarz, D. Stauffer, and K. Kulakowski, “Bonabeau model on a fully connected graph,” European Physical J. B, Vol.50, pp. 195-198, 2006. https://doi.org/10.1140/epjb/e2006-00059-3
28. [28] L. K. Gallos, “Self-organizing social hierarchies on scale-free networks,” Int. J. of Modern Physics C, Vol.16, No.08, pp. 1329-1336, 2005. https://doi.org/10.1142/S0129183105007935
29. [29] R. Asad, T. Hayakawa, and T. Yasuda, “Evolutionary Design of Cooperative Transport Behavior for a Heterogeneous Robotic Swarm,” J. Robot. Mechatron., Vol.35, No.4, pp. 1007-1015, 2023. https://doi.org/10.20965/jrm.2023.p1007