Paper:
Innovation Sharing Distributed Kalman Filter with Packet Loss
Shuo Huang and Kaoru Yamamoto

Faculty of Information Science and Electrical Engineering, Kyushu University
744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
This study investigates the problem of distributed state estimation. A distributed Kalman filter algorithm is proposed, in which sensors exchange their innovations. A detailed analysis is conducted for the case of two sensor networks, demonstrating that the proposed algorithm outperforms the case where each sensor runs a conventional Kalman filter without communication. The upper bounds of error covariance matrices are also derived in the case of packet loss. Numerical examples verify the effectiveness of the proposed algorithm.
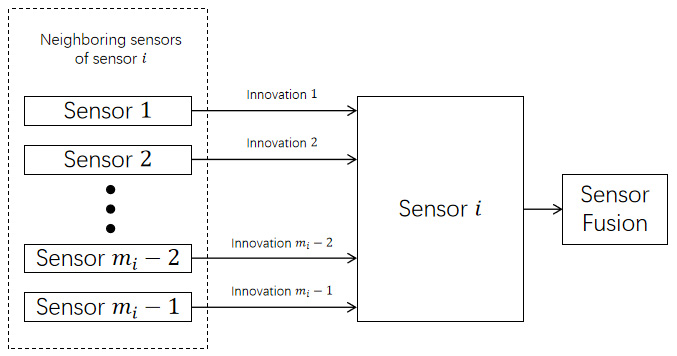
Conceptual diagram of distributed filtering
- [1] R. Olfati-Saber and J. S. Shamma, “Consensus filters for sensor networks and distributed sensor fusion,” Proc. of the 44th IEEE Conf. on Decision and Control, 2005. https://doi.org/10.1109/CDC.2005.1583238
- [2] R. Olfati-Saber, “Distributed Kalman filter with embedded consensus filters,” Proc. of the 44th IEEE Conf. on Decision and Control, 2005. https://doi.org/10.1109/CDC.2005.1583486
- [3] R. Olfati-Saber, “Distributed Kalman filtering for sensor network,” 2007 46th IEEE Conf. on Decision and Control, 2007.
- [4] S. Park and N. C. Martins, “Design of distributed LTI observers for state omniscience,” IEEE Trans. on Automatic Control, Vol.62, No.2, pp. 561-576, 2016. https://doi.org/10.1109/TAC.2016.2560766
- [5] A. Mitra and S. Shreyas, “Distributed observers for LTI systems,” IEEE Trans. on Automatic Control, Vol.63, No.11, pp. 3689-3704, 2018.
- [6] W. Han et al., “A simple approach to distributed observer design for linear systems,” IEEE Trans. on Automatic Control, Vol.64, No.1, pp. 329-336, 2018. https://doi.org/10.1109/TAC.2018.2828103
- [7] L. Wang and A. S. Morse, “A distributed observer for a time-invariant linear system,” IEEE Trans. on Automatic Control, Vol.63, No.7, pp. 2123-2130, 2017. https://doi.org/10.1109/TAC.2017.2768668
- [8] C. Yang et al., “Multi-sensor Kalman filtering with intermittent measurements,” IEEE Trans. on Automatic Control, Vol.63, No.3, pp. 797-804, 2018. https://doi.org/10.1109/TAC.2017.2734643
- [9] W. Li, Y. Jia, and J. Du, “Distributed Kalman consensus filter with intermittent observations,” J. of the Franklin Institute, Vol.352, No.9, pp. 3764-3781, 2015. https://doi.org/10.1016/j.jfranklin.2015.01.002
- [10] A. Tanwani, “Suboptimal filtering over sensor networks with random communication,” IEEE Trans. on Automatic Control, Vol.67, No.10, pp. 5456-5463, 2021. https://doi.org/10.1109/TAC.2021.3116180
- [11] H. Jin and S. Sun, “Distributed filtering for multi-sensor systems with missing data,” Information Fusion, Vols.86-87, pp. 116-135, 2022. https://doi.org/10.1016/j.inffus.2022.06.007
- [12] I. Matei and J. S. Baras, “Consensus-based linear distributed filtering,” Automatica, Vol.48, No.8, pp. 1776-1782, 2012. https://doi.org/10.1016/j.automatica.2012.05.042
- [13] R. Deshmukh, C. Kwon, and I. Hwang, “Optimal discrete-time Kalman consensus filter,” 2017 American Control Conf. (ACC), 2017. https://doi.org/10.23919/ACC.2017.7963859
- [14] Y. Shen and S. Sun, “Distributed recursive filtering for multi-rate uniform sampling systems with packet losses in sensor networks,” Int. J. of Systems Science, Vol.54, No.8, pp. 1729-1745, 2023. https://doi.org/10.1080/00207721.2023.2209887
- [15] D. Simon, “Optimal state estimation: Kalman, H infinity, and nonlinear approaches,” John Wiley & Sons, 2006.
- [16] R. E. Kalman, “A new approach to linear filtering and prediction problems,” J. Basic Eng., Vol.82, No.1, pp. 35-45, 1960. https://doi.org/10.1115/1.3662552
- [17] B. Sinopoli et al., “Kalman filtering with intermittent observations,” IEEE Trans. on Automatic Control, Vol.49, No.9, pp. 1453-1464, 2004. https://doi.org/10.1109/TAC.2004.834121
- [18] F. Zhang (Ed.), “The Schur complement and its applications,” Vol.4, Springer Science & Business Media, 2006. https://doi.org/10.1007/b105056
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.