Paper:
Noncooperative Population-Based Search Relying on Spatial and/or Temporal Scale-Free Behaviors of Individuals
Kei Ohnishi

Kyushu Institute of Technology
680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan
Although individuals of species engaging in cooperative foraging behaviors are often modeled as swarm intelligence optimization algorithms, there are also several species whose individuals take noncooperative foraging behaviors. Some such species exhibit common behaviors, which we call scale-free behaviors in this study. A type of scale-free behavior is spatial scale-free behavior, in which the moving distance of an individual from the present food source follows a power-law distribution. Second, the staying duration of an individual at the current food source follows a power-law distribution, and this behavior is called temporal scale-free behavior. We propose two types of noncooperative population-based search methods, based on the two types of scale-free behaviors. We also conducted simulations to compare the two methods, assuming static and dynamic environments in which the position of the food source did not change and changed, respectively. The simulation results showed that temporal scale-free behavior is suitable for specific problems in which individuals around the global optimum can be eliminated probabilistically, and spatial scale-free behavior is suitable for problems in which such elimination never occurs. In other words, the two types of scale-free behaviors are complementary. Next, we first assume problems for which we cannot know if the probabilistic elimination of individuals occurs in advance, and then propose a search method that selects an appropriate type of scale-free behavior for individuals during the search. The simulation results showed that this method demonstrates a good search performance, on average, for such problems.
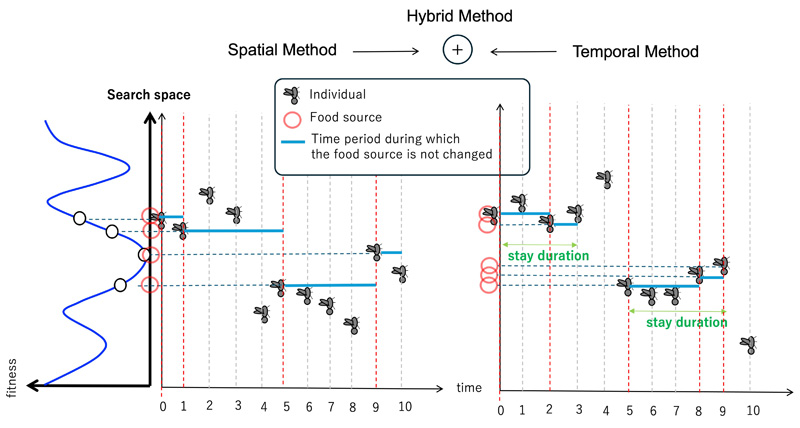
Three proposed methods
- [1] M. Dorigo, V. Maniezzo, and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Trans. on Systems, Man, and Cybernetics, Part B, Vol.26, No.1, pp. 29-41, 1996. https://doi.org/10.1109/3477.484436
- [2] D. Karaboga, “An idea based on honey bee swarm for numerical optimization,” Technical Report, TR06, Erciyes University, 2005.
- [3] K. Ohnishi, A. Fujiwara, and M. Koeppen, “Non-swarm intelligence search algorithm based on the foraging behaviors of fruit flies,” 2016 IEEE Congress on Evolutionary Computation (CEC), pp. 1509-1516, 2016. https://doi.org/10.1109/CEC.2016.7743968
- [4] I. Shimada, Y. Kawazoe, and H. Hara, “A temporal model of animal behavior based on a fractality in the feeding of Drosophila melanogaster,” Biological Cybernetics, Vol.68, No.6, pp. 477-481, 1993. https://doi.org/10.1007/BF00200806
- [5] M. Koganezawa, H. Hara, Y. Hayakawa, and I. Shimada, “Memory effects on scale-free dynamics in foraging Drosophila,” J. of Theoretical Biology, Vol.260, No.3, pp. 353-358, 2009. https://doi.org/10.1016/j.jtbi.2009.06.018
- [6] G. M. Viswanathan et al., “Lévy flight search patterns of wandering albatrosses,” Nature, Vol.381, No.6581, pp. 413-415, 1996. https://doi.org/10.1038/381413a0
- [7] G. M. Viswanathan et al., “Optimizing the success of random searches,” Nature, Vol.401, No.6756, pp. 911-914, 1999. https://doi.org/10.1038/44831
- [8] A. M. Reynolds, A. D. Smith, D. R. Reynolds, N. L. Carreck, and J. L. Osborne, “Honeybees perform optimal scale-free searching flights when attempting to locate a food source,” J. of Experimental Biology, Vol.210, Vol.21, pp. 3763-3770, 2007. https://doi.org/10.1242/jeb.009563
- [9] M. F. Shlesinger and J. Klafter, “Lévy walks versus Lévy flights,” H. E. Stanley and N. Ostrowsky (Eds.), “On Growth and Form: Fractal and Non-Fractal Patterns in Physics,” pp. 279-283, Kluwer Academic Publishers, 1985.
- [10] X.-S. Yang and S. Deb, “Cuckoo Search via Lévy flights,” 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), pp. 210-214, 2009. https://doi.org/10.1109/NABIC.2009.5393690
- [11] X.-S. Yang, “Firefly algorithm, Lévy flights and global optimization,” M. Bramer, R. Ellis, and M. Petridis (Eds.), “Research and Development in Intelligent Systems XXVI,” pp. 209-218, Springer, 2010. https://doi.org/10.1007/978-1-84882-983-1_15
- [12] H. Sharma, J. C. Bansal, and K. V. Arya, “Opposition based Lévy flight artificial bee colony,” Memetic Computing, Vol.5, No.3, pp. 213-227, 2013. https://doi.org/10.1007/s12293-012-0104-0
- [13] A. Aswale, A. López, A. Ammartayakun, and C. Pinciroli, “Hacking the colony: On the disruptive effect of misleading pheromone and how to defend against it,” Proc. of the 21st Int. Conf. on Autonomous Agents and Multiagent Systems (AAMAS’22), pp. 27-34, 2022.
- [14] F. Uwano, Y. Tajima, A. Murata, and K. Takadama, “Recovery system based on exploration-biased genetic algorithm for stuck rover in planetary exploration,” J. Robot. Mechatron., Vol.29, No.5, pp. 877-886, 2017. https://doi.org/10.20965/jrm.2017.p0877
- [15] V. Verma et al., “Autonomous robotics is driving Perseverance rover’s progress on Mars,” Science Robotics, Vol.8, No.80, Article No.eadi3099, 2023. https://doi.org/10.1126/scirobotics.adi3099
- [16] J. V. Hook et al., “Multirobot onsite shared analytics information and computing,” IEEE Trans. on Control of Network Systems, Vol.10, No.1, pp. 169-181, 2023. https://doi.org/10.1109/TCNS.2022.3198789
- [17] A. Akemoto and F. Zhu, “Cooperative lunar surface exploration using transfer learning with multi-agent visual teach and repeat,” 2023 IEEE Aerospace Conf., 2023. https://doi.org/10.1109/AERO55745.2023.10115696
- [18] V. S. Chirala, K. Sundar, S. Venkatachalam, J. M. Smereka, and S. Kassoumeh, “Heuristics for multi-vehicle routing problem considering human-robot interactions,” IEEE Trans. on Intelligent Vehicles, Vol.8, No.5, pp. 3228-3238, 2023. https://doi.org/10.1109/TIV.2023.3261274
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.