Top > JRM > An Admittance Controller with a Jerk Limiter for Position-Cont ...

single-rb.php

JRM Vol.36 No.2 pp. 483-493
doi: 10.20965/jrm.2024.p0483
(2024)

Paper:

Views over last 60 days: 78

An Admittance Controller with a Jerk Limiter for Position-Controlled Robots

Ryusei Mae ORCID Icon and Ryo Kikuuwe ORCID Icon

Machinery Dynamics Laboratory, Hiroshima University
1-4-1 Kagamiyama, Higashi-hiroshima, Hiroshima 739-8527, Japan

Received:
July 3, 2023
Accepted:
January 31, 2024
Published:
April 20, 2024
Creative Commons License
Keywords:
admittance control, jerk limiter, vibration suppression, normal cone, differential inclusion
Abstract

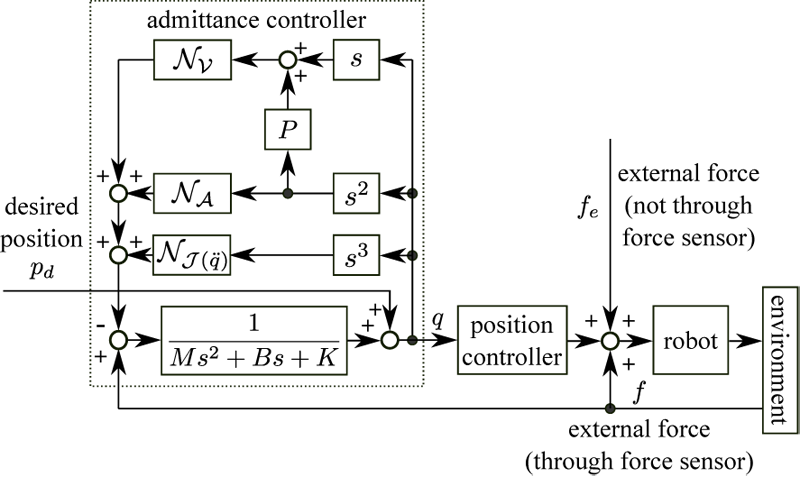
This paper proposes an admittance control scheme for robots equipped with joint-level position controllers involving deadtime. Its main feature is an elaborate discrete-time jerk limiter, which limits the third derivative of the position command sent to the controller. The jerk limiter is designed to suppress undesirable oscillation especially when the robot is in contact with a stiff environment. The controller is designed as a differential inclusion involving normal cones in the continuous-time domain, and its discrete-time algorithm is derived by the implicit Euler discretization. The presented controller was validated with experiments using a collaborative robot UR3e of Universal Robots, which has a deadtime of 6 ms in the velocity-command mode.

A robot controlled with the proposed admittance controller

A robot controlled with the proposed admittance controller

Cite this article as:
R. Mae and R. Kikuuwe, “An Admittance Controller with a Jerk Limiter for Position-Controlled Robots,” J. Robot. Mechatron., Vol.36 No.2, pp. 483-493, 2024.
Data files:
References
  1. [1] D. A. Lawrence, “Impedance control stability properties in common implementations,” Proc. of 1988 IEEE Int. Conf. on Robotics and Automation, Vol.2, pp. 1185-1190, 1988. https://doi.org/10.1109/ROBOT.1988.12222
  2. [2] C. T. Landi et al., “Variable admittance control preventing undesired oscillating behaviors in physical human-robot interaction,” 2017 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 3611-3616, 2017. https://doi.org/10.1109/IROS.2017.8206207
  3. [3] Y. Sun et al., “Adaptive admittance control for safety-critical physical human robot collaboration,” IFAC-PapersOnLine, Vol.56, No.2, pp. 1313-1318, 2023. https://doi.org/10.1016/j.ifacol.2023.10.1772
  4. [4] T. Sun, Z. Wang, C. He, and L. Yang, “Adaptive robust admittance control of robots using duality principle-based impedance selection,” Applied Sciences, Vol.12, No.23, Article No.12222, 2022. https://doi.org/10.3390/app122312222
  5. [5] C. T. Landi, F. Ferraguti, L. Sabattini, C. Secchi, and C. Fantuzzi, “Admittance control parameter adaptation for physical human-robot interaction,” 2017 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 2911-2916, 2017. https://doi.org/10.1109/ICRA.2017.7989338
  6. [6] F. Dimeas and N. Aspragathos, “Online stability in human-robot cooperation with admittance control,” IEEE Trans. on Haptics, Vol.9, No.2, pp. 267-278, 2016. https://doi.org/10.1109/TOH.2016.2518670
  7. [7] B. Yao et al., “Sensorless and adaptive admittance control of industrial robot in physical human-robot interaction,” Robotics and Computer-Integrated Manufacturing, Vol.51, pp. 158-168, 2018. https://doi.org/10.1016/j.rcim.2017.12.004
  8. [8] G. Kang, H. S. Oh, J. K. Seo, U. Kim, and H. R. Choi, “Variable admittance control of robot manipulators based on human intention,” IEEE/ASME Trans. on Mechatronics, Vol.24, No.3, pp. 1023-1032, 2019. https://doi.org/10.1109/TMECH.2019.2910237
  9. [9] F. Ferraguti et al., “A variable admittance control strategy for stable physical human–robot interaction,” The Int. J. of Robotics Research, Vol.38, No.6, pp. 747-765, 2019. https://doi.org/10.1177/0278364919840415
  10. [10] Z. Chen, Q. Guo, T. Li, Y. Yan, and D. Jiang, “Gait prediction and variable admittance control for lower limb exoskeleton with measurement delay and extended-state-observer,” IEEE Trans. on Neural Networks and Learning Systems, Vol.34, No.11, pp. 8693-8706, 2023. https://doi.org/10.1109/TNNLS.2022.3152255
  11. [11] C. Liu, Y. He, X. Chen, and H. Cao, “Adaptive enhanced admittance force-tracking controller design for highly dynamic interactive tasks,” Industrial Robot, Vol.49, No.5, pp. 903-912, 2022. https://doi.org/10.1108/IR-10-2021-0222
  12. [12] K. Haninger, M. Radke, A. Vick, and J. Krüger, “Towards high-payload admittance control for manual guidance with environmental contact,” IEEE Robotics and Automation Letters, Vol.7, No.2, pp. 4275-4282, 2022. https://doi.org/10.1109/LRA.2022.3150051
  13. [13] R. Kikuuwe, “A sliding-mode-like position controller for admittance control with bounded actuator force,” IEEE/ASME Trans. on Mechatronics, Vol.19, No.5, pp. 1489-1500, 2014. https://doi.org/10.1109/TMECH.2013.2286411
  14. [14] R. Kikuuwe, “Torque-bounded admittance control realized by a set-valued algebraic feedback,” IEEE Trans. on Robotics, Vol.35, No.5, pp. 1136-1149, 2019. https://doi.org/10.1109/TRO.2019.2920069
  15. [15] M. T. S. Aung and R. Kikuuwe, “Stability enhancement of admittance control with acceleration feedback and friction compensation,” Mechatronics, Vol.45, pp. 110-118, 2017. https://doi.org/10.1016/j.mechatronics.2017.06.011
  16. [16] Y. Aydin, O. Tokatli, V. Patoglu, and C. Basdogan, “Stable physical human-robot interaction using fractional order admittance control,” IEEE Trans. on Haptics, Vol.11, No.3, pp. 464-475, 2018. https://doi.org/10.1109/TOH.2018.2810871
  17. [17] Y. Aydin, O. Tokatli, V. Patoglu, and C. Basdogan, “Fractional order admittance control for physical human-robot interaction,” 2017 IEEE World Haptics Conf. (WHC), pp. 257-262, 2017. https://doi.org/10.1109/WHC.2017.7989911
  18. [18] K. Li, Y. He, K. Li, and C. Liu, “Adaptive fractional-order admittance control for force tracking in highly dynamic unknown environments,” Industrial Robot, Vol.50, No.3, pp. 530-541, 2023. https://doi.org/10.1108/IR-09-2022-0244
  19. [19] A. Morbi and M. Ahmadi, “Safely rendering small impedances in admittance-controlled haptic devices,” IEEE/ASME Trans. on Mechatronics, Vol.21, No.3, pp. 1272-1280, 2016. https://doi.org/10.1109/TMECH.2015.2506994
  20. [20] A. Lecours and C. Gosselin, “Computed-torque control of a four-degree-of-freedom admittance controlled intelligent assist device,” J. P. Desai, G. Dudek, O. Khatib, and V. Kumar (Eds.), “Experimental Robotics: The 13th International Symposium on Experimental Robotics,” pp. 635-649, Springer, 2013. https://doi.org/10.1007/978-3-319-00065-7_43
  21. [21] R. Kikuuwe and B. Brogliato, “A new representation of systems with frictional unilateral constraints and its Baumgarte-like relaxation,” Multibody System Dynamics, Vol.39, No.3, pp. 267-290, 2017. https://doi.org/10.1007/s11044-015-9491-6
  22. [22] B. Brogliato, A. Daniilidis, C. Lemaréchal, and V. Acary, “On the equivalence between complementarity systems, projected systems and differential inclusions,” Systems & Control Letters, Vol.55, No.1, pp. 45-51, 2006. https://doi.org/10.1016/j.sysconle.2005.04.015
  23. [23] V. Acary and B. Brogliato, “Numerical Methods for Nonsmooth Dynamical Systems: Applications in Mechanics and Electronics,” Springer, 2008. https://doi.org/10.1007/978-3-540-75392-6
  24. [24] H. H. Bauschke and P. L. Combettes, “Convex Analysis and Monotone Operator Theory in Hilbert Spaces,” 2nd edition, Springer, 2017. https://doi.org/10.1007/978-3-319-48311-5
  25. [25] H. K. Khalil, “Nonlinear Systems,” 3rd edition, Prentice Hall, 2002.
  26. [26] J.-J. E. Slotine and W. Li, “Applied Nonlinear Control,” Prentice Hall, 1990.

Creative Commons License  This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.

*This site is desgined based on HTML5 and CSS3 for modern browsers, e.g. Chrome, Firefox, Safari, Edge, Opera.

Last updated on May. 01, 2024