Paper:
Quantitative Analysis of the Coordinated Movement of Cells in a Freely Moving Cell Population
Daiki Umetsu*
 , Satoshi Yamaji**,***, Daiki Wakita**
, Satoshi Yamaji**,***, Daiki Wakita**
 , and Takeshi Kano**
, and Takeshi Kano**

*Graduate School of Science, Osaka University
1-1 Machikaneyama, Toyonaka, Osaka 560-0043, Japan
**Research Institute of Electrical Communication, Tohoku University
2-1-1 Katahira, Aoba-ku, Sendai, Miyagi 980-8577, Japan
***Graduate School of Engineering, Tohoku University
6-6-01 Aramaki Aza-Aoba, Aoba-ku, Sendai, Miyagi 980-8579, Japan
Coordinated movement of self-propelled agents has been well studied in collectives or swarms that display directional movement. Self-propelled agents also develop stable spatial patterns in which the agents do not necessarily exhibit directional collective movement. However, quantitative measures that are required to analyze the local and temporal coordinated movements during pattern formation processes have not been well established. Here, we study the coordinated movement of individual pairs of two different types of cells in a freely moving cell population. We introduced three criteria to evaluate coordinated movement in live imaging data obtained from the abdomen of the fruit fly, Drosophila melanogaster, at the pupal stage. All three criteria were able to reasonably identify coordinated movement. Our analysis indicates that the combined usage of these criteria can improve the evaluation of whether a pair of cells exhibits coordinated movement or not by excluding false positives. Quantitative approaches to identifying coordinated movement in a population of freely moving agents constitute a key foundational methodology to study pattern formations by self-propelled agents.
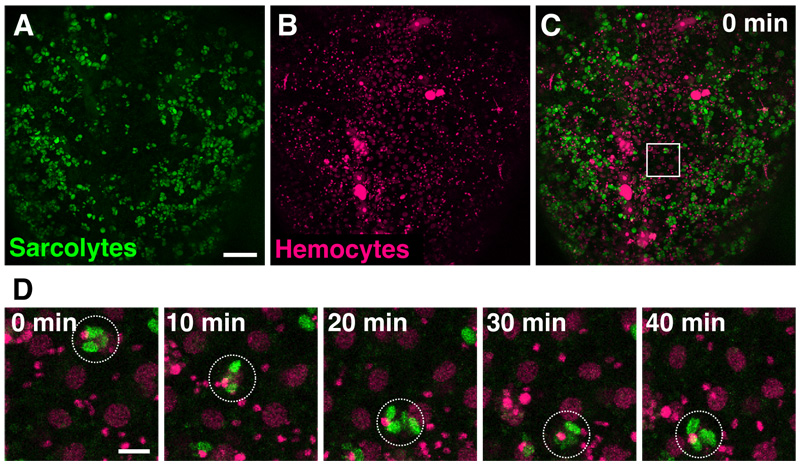
Coordinated movement of migrating cells
- [1] T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, “Novel type of phase transition in a system of self-driven particles,” Phys. Rev. Lett., Vol.75, No.6, pp. 1226-1229, 1995. https://doi.org/10.1103/PhysRevLett.75.1226
- [2] A. Cavagna et al., “Scale-free correlations in starling flocks,” Proc. Natl. Acad. Sci., Vol.107, No.26, pp. 11865-11870, 2010. https://doi.org/10.1073/pnas.1005766107
- [3] K. Tunstrøm et al., “Collective states, multistability and transitional behavior in schooling fish,” PLOS Comput. Biol., Vol.9, No.2, Article No.e1002915, 2013. https://doi.org/10.1371/journal.pcbi.1002915
- [4] S. Tanaka, S. Nakata, and T. Kano, “Dynamic ordering in a swarm of floating droplets driven by solutal Marangoni effect,” J. Phys. Soc. Jpn., Vol.86, No.10, Article No.101004, 2017. https://doi.org/10.7566/JPSJ.86.101004
- [5] A. Nakamasu, G. Takahashi, A. Kanbe, and S. Kondo, “Interactions between zebrafish pigment cells responsible for the generation of Turing patterns,” Proc. Natl. Acad. Sci., Vol.106, No.21, pp. 8429-8434, 2009. https://doi.org/10.1073/pnas.0808622106
- [6] K. H. Palmquist et al., “Reciprocal cell-ECM dynamics generate supracellular fluidity underlying spontaneous follicle patterning,” Cell, Vol.185, No.11, pp. 1960-1973, 2022. https://doi.org/10.1016/j.cell.2022.04.023
- [7] A. E. Shyer et al., “Emergent cellular self-organization and mechanosensation initiate follicle pattern in the avian skin,” Science, Vol.357, No.6353, pp. 811-815, 2017. https://doi.org/10.1126/science.aai7868
- [8] T. Sugi, H. Ito, M. Nishimura, and K. H. Nagai, “C. elegans collectively forms dynamical networks,” Nat. Commun., Vol.10, Article No.683, 2019. https://doi.org/10.1038/s41467-019-08537-y
- [9] H. Haga, C. Irahara, R. Kobayashi, T. Nakagaki, and K. Kawabata, “Collective movement of epithelial cells on a collagen gel substrate,” Biophys. J., Vol.88, No.3, pp. 2250-2256, 2005. https://doi.org/10.1529/biophysj.104.047654
- [10] M. Ballerini et al., “Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study,” Proc. Natl. Acad. Sci., Vol.105, No.4, pp. 1232-1237, 2008. https://doi.org/10.1073/pnas.0711437105
- [11] B. Slater, C. Londono, and A. P. McGuigan, “An algorithm to quantify correlated collective cell migration behavior,” BioTechniques, Vol.54, No.2, pp. 87-92, 2013. https://doi.org/10.2144/000113990
- [12] Y. Kuleesha, W. C. Puah, and M. Wasser, “A model of muscle atrophy based on live microscopy of muscle remodelling in Drosophila metamorphosis,” R. Soc. Open Sci., Vol.3, No.2, Article No.150517, 2016. https://doi.org/10.1098/rsos.150517
- [13] S. Ghosh, S. Ghosh, and L. Mandal, “Drosophila metamorphosis involves hemocyte mediated macroendocytosis and efferocytosis,” Int. J. Dev. Biol., Vol.64, Nos.4-6, pp. 319-329, 2020. https://doi.org/10.1387/ijdb.190215lm
- [14] A. E. B. T. King and M. S. Turner, “Non-local interactions in collective motion,” R. Soc. Open Sci., Vol.8, No.3, Article No.201536, 2021. https://doi.org/10.1098/rsos.201536
- [15] A. J. Kabla, “Collective cell migration: Leadership, invasion and segregation,” J. R. Soc. Interface, Vol.9, No.77, pp. 3268-3278, 2012. https://doi.org/10.1098/rsif.2012.0448
- [16] R. Gorelik and A. Gautreau, “Quantitative and unbiased analysis of directional persistence in cell migration,” Nat. Protoc., Vol.9, No.8, pp. 1931-1943, 2014. https://doi.org/10.1038/nprot.2014.131
- [17] C.-M. Svensson, A. Medyukhina, I. Belyaev, N. Al-Zaben, and M. T. Figge, “Untangling cell tracks: Quantifying cell migration by time lapse image data analysis,” Cytometry Part A, Vol.93, No.3, pp. 357-370, 2018. https://doi.org/10.1002/cyto.a.23249
- [18] W. Wood and P. Martin, “Macrophage functions in tissue patterning and disease: New insights from the fly,” Dev. Cell, Vol.40, No.3, pp. 221-233, 2017. https://doi.org/10.1016/j.devcel.2017.01.001
- [19] M. Coppola, J. Guo, E. Gill, and G. C. H. E. de Croon, “Provable self-organizing pattern formation by a swarm of robots with limited knowledge,” Swarm Intell., Vol.13, No.1, pp. 59-94, 2019. https://doi.org/10.1007/s11721-019-00163-0
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.