Letter:
Identification of Shaft Stiffness and Inertias in Flexible Drive Systems
Rached Dhaouadi and Ishaq Hafez
College of Engineering, American University of Sharjah
P.O. Box 26666, Sharjah, UAE
This letter presents an identification method for motor drive systems with flexible shafts and couplings using frequency response measurement. The drive system can be approximated as a two-mass non-rigid mechanical system to model the lowest resonant frequency with three parameters to be identified: the motor side inertia, the load side inertia, and the shaft stiffness. The proposed method does not require knowledge of the total inertia as many other techniques require. However, additional known inertia is added or removed from the load side assembly. The frequency response measurement is carried out with and without additional inertia to identify the resonant and anti-resonant frequencies. It is shown that this procedure directly identifies the two inertias and shaft stiffness and can be utilized to assist in the commissioning of electrical drives.
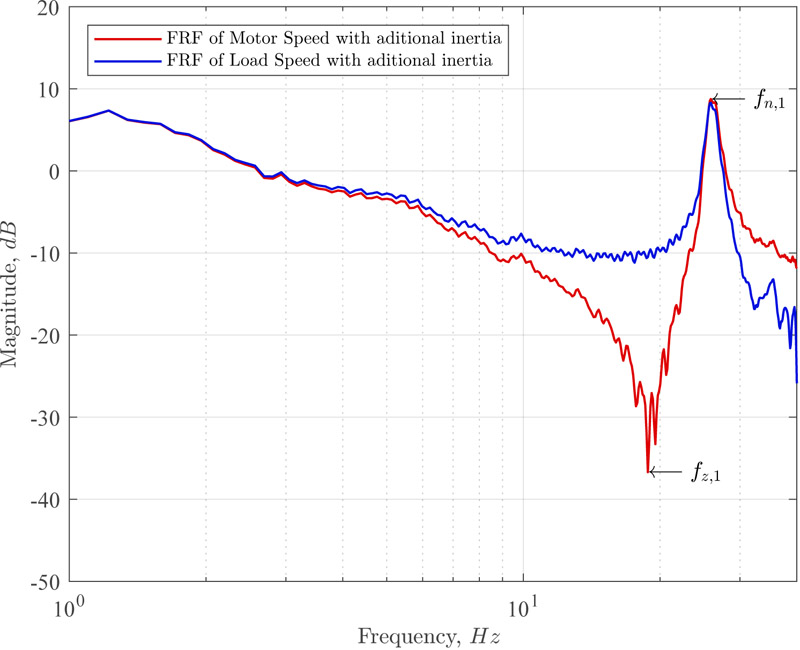
Frequency response of the 2MM system
- [1] A. H. Jafari, R. Dhaouadi, and A. Jhemi, “Nonlinear Friction Estimation in Elastic Drive Systems Using a Dynamic Neural Network-Based Observer,” J. Adv. Comput. Intell. Intell. Inform., Vol.17, No.4, pp. 637-646, 2013.
- [2] C. Shao, J. Togashi, K. Mitobe, and G. Capi, “Utilizing the Nonlinearity of Tendon Elasticity for Compensation of Unknown Gravity of Payload,” J. Robot. Mechatron., Vol.30, No.6, pp. 873-879, 2018.
- [3] H. Muramoto, K. Tomita, and T. Morita, “Compliance Analysis of Construction Machinery Front by Direct Stiffness Method,” J. Robot. Mechatron., Vol.20, No.3, pp. 481-489, 2008.
- [4] K. Sakaguchi, T. Sudo, N. Bushida, Y. Chiba, Y. Asai, and K. Kikuchi, “Wheel-Based Stair Climbing Robot with Hopping Mechanism – Fast Stair Climbing and Soft Landing Using Vibration of 2-DOF System –,” J. Robot. Mechatron., Vol.19, No.3, pp. 258-263, 2007.
- [5] F. Schütte, S. Beineke, H. Grotstollen, N. Fröhleke, U. Witkowski, U. Rückert, and S. Rüping, “Structure-and parameter identification for a two-mass-system with backlash and friction using a self-organizing map,” European Conf. on Power Electronics and Applications, Vol.3, pp. 3358-3363, 1997.
- [6] S. Villwock and M. Pacas, “Application of the Welch-Method for the Identification of Two- and Three-Mass-Systems,” IEEE Trans. on Industrial Electronics, Vol.55, No.1, pp. 457-466, 2008.
- [7] R. Dhaouadi and K. Kubo, “Transfer function and parameters identification of a motor drive system using adaptive filtering,” Proc. of 4th IEEE Int. Workshop on Advanced Motion Control (AMC’96 – MIE), Vol.2, pp. 588-593, 1996.
- [8] H. Loussifi, K. Nouri, and N. B. Braiek, “Assessment of the continuous wavelet transform in the modal parameters estimation of 2MM and 3MM systems,” IEEJ Trans. on Electrical and Electronic Engineering, Vol.7, No.S1, pp. S86-S95, 2012.
- [9] R. Sato, Y. Ito, S. Mizuura, and K. Shirase, “Vibration Mode and Motion Trajectory Simulations of an Articulated Robot by a Dynamic Model Considering Joint Bearing Stiffness,” Int. J. Automation Technol., Vol.15, No.5, pp. 631-640, 2021.
- [10] S. Tsuruhara and K. Ito, “Data-Driven Model-Free Adaptive Displacement Control for Tap-Water-Driven Artificial Muscle and Parameter Design Using Virtual Reference Feedback Tuning,” J. Robot. Mechatron., Vol.34, No.3, pp. 664-676, 2022.
- [11] D. Waleed, H. M. Usman, and R. Dhaouadi, “Dynamic Friction Characterization of a Linear Servo Motor Using an Optimal Sinusoidal Reference Tracking Controller,” J. Robot. Mechatron., Vol.30, No.6, pp. 1014-1018, 2018.
- [12] R. Dhaouadi, “Torque Control in Harmonic Drives with Nonlinear Dynamic Friction Compensation,” J. Robot. Mechatron., Vol.16, No.4, pp. 388-396, 2004.
- [13] I. Hafez and R. Dhaouadi, “Application of Particle Swarm Optimization for the Identification of Two-Mass Electric Drive Systems,” 2022 8th Int. Conf. on Control, Decision and Information Technologies (CoDIT), Vol.1, pp. 758-763, 2022.
- [14] R. Pintelon and J. Schoukens, “Measurement of Frequency Response Functions – Standard Solutions,” Chapter 2, pp. 33-72, John Wiley & Sons, Ltd., 2012.
- [15] E. A. Medina B, “Multi-input, multi-output system identification from frequency response samples with applications to the modeling of large space structures,” Master’s thesis, Ohio University, 1991.
- [16] S. Orlando, B. Peeters, and G. Coppotelli, “Improved FRF estimators for MIMO sine sweep data,” 23rd Int. Conf. on Noise and Vibration Engineering 2008 (ISMA 2008), Vol.2, 2008.
- [17] T. W. Corke, N. F. Betzler, E. S. Wallace, M. Strangwood, and S. R. Otto, “Implications of Rigid Gripping Constraints on Clubhead Dynamics in Steel Golf Shafts,” Applied Sciences, Vol.8, No.3, Article No.422, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.