Paper:
Moving Particle Semi-Implicit and Finite Element Method Coupled Analysis for Brain Shift Estimation
Akito Ema*1, Xiaoshuai Chen*2, Kazuya Sase*3, Teppei Tsujita*4, and Atsushi Konno*1
*1Graduate School of Information Science and Technology, Hokkaido University
Kita 14, Nishi 9, Kita-ku, Sapporo, Hokkaido 060-0814, Japan
*2Graduate School of Science and Technology, Hirosaki University
3 Bunkyo-cho, Hirosaki, Aomori 036-8560, Japan
*3Faculty of Engineering, Tohoku Gakuin University
1-13-1 Chuo, Tagajo, Miyagi 980-8511, Japan
*4Department of Mechanical Engineering, National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
Neuronavigation is a computer-assisted technique for presenting three-dimensional images of a patient’s brain to facilitate immediate and precise lesion localization by surgeons. Neuronavigation systems use preoperative medical images of patients. In neurosurgery, when the dura mater and arachnoid membrane are incised and the cerebrospinal fluid (CSF) drains out, the brain loses the CSF buoyancy and deforms in the direction of gravity, which is referred to as brain shift. This brain shift yields inaccurate neuronavigation. To reduce this inaccuracy, an intraoperative brain shift should be estimated. This paper proposes a dynamic simulation method for brain-shift estimation combining the moving-particle semi-implicit (MPS) method and the finite element method (FEM). The CSF was modeled using fluid particles, whereas the brain parenchyma was modeled using finite elements (FEs). Node particles were attached to the surface nodes of the brain parenchyma in the FE model. The interaction between the CSF and brain parenchyma was simulated using the repulsive force between the fluid particles and node particles. Validation experiments were performed using a gelatin block. The gelatin block was dipped into silicone oil, which was then gradually removed; the block deformation owing to the buoyancy loss was measured. The experimental deformation data were compared with the results of the MPS-FEM coupled analysis. The mean absolute error (MAE) between the simulated deformation and the average across the four experiments was 0.26 mm, while the mean absolute percentage error (MAPE) was 27.7%. Brain-shift simulations were performed using the MPS-FEM coupled analysis, and the computational cost was evaluated.
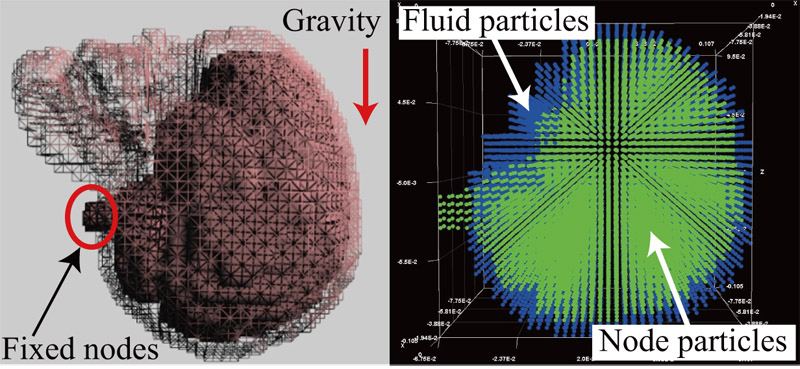
Brain shift simulation using MPS-FEM coupled analysis
- [1] E. Watanabe, T. Watanabe, S. Manaka, Y. Mayanagi, and K. Takakura, “Three-dimensional digitizer (neuronavigator): New equipment for computed tomography-guided stereotaxic surgery,” Surgical Neurology, Vol.27, No.6, pp. 543-547, 1987.
- [2] E. Watanabe, M. Satoh, T. Konno, M. Hirai, and T. Yamaguchi, “The Trans-Visible Navigator: A See-Through Neuronavigation System Using Augmented Reality,” World Neurosurgery, Vol.87, pp. 399-405, 2016.
- [3] A. Nabavi, P. M. Black, D. T. Gering, C.-F. Westin, V. Mehta, J. Richard, S. Pergolizzi, M. Ferrant, S. K. Warfield, N. Hata, R. B. Schwartz, W. M. Wells, R. Kikinis, and F. A. Jolesz, “Serial Intraoperative Magnetic Resonance Imaging of Brain Shift,” Neurosurgery, Vol.48, No.4, pp. 787-798, 2001.
- [4] D. W. Roberts, A. Hartov, F. E. Kennedy, M. I. Miga, and K. D. Paulsen, “Intraoperative brain shift and deformation: a quantitative analysis of cortical displacement in 28 cases,” Neurosurgery, Vol.43, No.4, pp. 749-758, 1998.
- [5] D. L. Hill, C. R. Maurer, R. J. Maciunas, R. J. Maciunas, J. A. Barwise, J. M. Fitzpatrick, and M. Y. Wang, “Measurement of intraoperative brain surface deformation under a craniotomy,” Neurosurgery, Vol.43, No.3, pp. 514-526, 1998.
- [6] M. Bucki, C. Lobos, and Y. Payan, “Framework for a low-cost intra-operative image-guided neuronavigator including brain shift compensation,” Annual Int. Conf. of the IEEE Engineering in Medicine & Biology Society, Vol.11, No.4, pp. 872-875, 2007.
- [7] A. Bilger, E. Bardinet, S. Fernández-Vidal, C. Duriez, P. Jannin, and S. Cotin, “Intra-operative Registration for Deep Brain Stimulation Procedures based on a Full Physics Head Model,” MICCAI 2014 Workshop on Deep Brain Stimulation Methodological Challenges – 2nd edition, Boston, United States, 2014.
- [8] D. X. Zhuang, Y. X. Liu, J. S. Wu, C. J. Yao, Y. Mao, C. X. Zhang, M. N. Wang, W. Wang, and L. F. Zhou, “A sparse intraoperative data-driven biomechanical model to compensate for brain shift during neuronavigation,” American J. of Neuroradiology, Vol.32, No.2, pp. 395-402, 2011.
- [9] A. E. Forte, S. Galvan, and D. Dini, “Models and tissue mimics for brain shift simulations,” Biomechanics and Modeling in Mechanobiology, Vol.17, No.1, pp. 249-261, 2018.
- [10] C. W. Hirt, A. A. Amsden, and J. L. Cook, “An arbitrary Lagrangian-Eulerian computing method for all flow speeds,” J. of Computational Physics, Vol.14, No.3, pp. 227-253, 1974.
- [11] S. Koshizuka and Y. Oka, “Moving-particle semi-implicit method for fragmentation of incompressible fluid,” Nuclear Science and Engineering, Vol.123, No.3, pp. 421-434, 1996.
- [12] L. B. Lucy, “A numerical approach to the testing of the fission hypothesis,” The Astronomical J., Vol.82, No.12, pp. 1013-1024, 1977.
- [13] J. J. Monaghan, “An introduction to SPH,” Computer Physics Communications, Vol.48, pp. 89-96, 1988.
- [14] S. Koshizuka, K. Shibata, M. Kondo, and T. Matsunaga, “Moving Particle Semi-Implicit Method – A Meshfree Particle Method for Fluid Dynamics,” Academic Press, 2018.
- [15] N. Mitsume, S. Yoshimura, K. Murotani, and T. Yamada, “MPS-FEM partitioned coupling approach for fluid-structure interaction with free surface flow,” Int. J. of Computational Methods, Vol.11, No.4, Article No.1350101, 2014.
- [16] M. M. Müller, J. Dorsey, L. McMillan, R. Jagnow, and B. Cutler, “Stable Real-Time Deformations,” Proc. of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, pp. 49-54, 2002.
- [17] A. Shakibaeinia and Y.-C. Jin, “A weakly compressible MPS method for modeling of open-boundary free-surface flow,” Int. J. for Numerical Methods in Fluids, Vol.63, No.10, pp. 1208-1232, 2010.
- [18] X. Chen, K. Sase, A. Konno, T. Tsujita, and S. Komizunai, “A simple damage and fracture model of brain parenchyma for haptic brain surgery simulations,” J. of Biomechanical Science and Engineering, Vol.11, No.4, Article No.16-00323, 2016.
- [19] K. Sase, A. Fukuhara, T. Tsujita, and A. Konno, “GPU-accelerated surgery simulation for opening a brain fissure,” ROBOMECH J., Vol.2, Article No.17, 2015.
- [20] N. M. Newmark, “A method of computation for structural dynamics,” Proc. ASCE, Vol.85, pp. 67-94, 1959.
- [21] X. Chen, R. Shirai, K. Masamune, M. Tamura, Y. Muragaki, K. Sase, T. Tsujita, and A. Konno, “Numerical Calculation Method for Brain Shift Based on Hydrostatics and Dynamic FEM,” IEEE Trans. on Medical Robotics and Bionics, Vol.4, No.2, pp. 368-380, 2022.
- [22] B. Rashid, M. Destrade, and M. Gilchrist, “Mechanical characterization of brain tissue in compression at dynamic strain rates,” J. of the Mechanical Behavior of Biomedical Materials, Vol.10, pp. 23-38, 2012.
- [23] A. C. Lui, T. Z. Polis, and N. J. Cicutti, “Densities of cerebrospinal fluid and spinal anaesthetic solutions in surgical patients at body temperature,” Canadian J. of Anaesthesia, Vol.45, No.4, pp. 297-303, 1998.
- [24] X. Chen, R. Shirai, K. Masamune, M. Tamura, Y. Muragaki, and A. Konno, “Presenting a Simple Method of Brain Shift Estimation for Neuronavigations and Considering its Practicality,” 2019 IEEE/SICE Int. Symposium on System Integration (SII2019), pp. 112-117, 2019.
- [25] M. Nakayama, S. Abiko, X. Jiang, A. Konno, and M. Uchiyama, “Stable Soft-Tissue Fracture Simulation for Surgery Simulator,” J. Robot. Mechatron., Vol.23, No.4, pp. 589-597, 2011.
- [26] X. Chen, K. Sase, T. Tsujita, and A. Konno, “A Nonlinear and Failure Numerical Calculation Method for Vessel Preservation Simulations based on Subarachnoid Space Structure Considerations,” IEEE Trans. on Medical Robotics and Bionics, Vol.2, No.3, pp. 356-363, 2020.
- [27] A. Fukuhara, T. Tsujita, K. Sase, A. Konno, X. Jiang, S. Abiko, and M. Uchiyama, “Proposition and evaluation of a collision detection method for real time surgery simulation of opening a brain fissure,” ROBOMECH J., Vol.1, Article No.6, 2014.
- [28] K. Sase, T. Tsujita, and A. Konno, “Embedding Segmented Volume in Finite Element Mesh with Topology Preservation,” S. Ourselin, L. Joskowicz, M. Sabuncu, G. Unal, and W. Wells (Eds.), Medical Image Computing and Computer-Assisted Intervention (MICCAI), Lecture Notes in Computer Science, Vol.9902, pp. 116-123, 2016.
- [29] K. Sase, T. Tsujita, and A. Konno, “Haptic Interaction with Segmented Medical Image Embedded in Finite Element Mesh,” J. of Japan Society of Computer Aided Surgery, Vol.19, No.2, pp. 89-99, 2017.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.