Paper:
Grid-Based Estimation of Transformation Between Partial Relationships Using a Genetic Algorithm
Sota Nakamura, Yuichi Kobayashi, and Taisei Matsuura
Shizuoka University
3-5-1 Johoku, Naka-ku, Hamamatsu 432-8561, Japan
Human motor learning is characterized by adaptation, wherein information obtained in the past is transferred to a different situation. In this study, we investigate a grid-based computation for explaining the reuse of the information of an existing controller for adaptation to a partial malfunction of a controller. To this end, a motor learning scheme is adopted based on the detection and estimation of partial relationships. The transformation between the partial relationships is estimated based on a grid-based estimation of the two coordinate systems. In this estimation, the coordinate systems are optimized using a genetic algorithm. Two arms in a reflection are considered, and it is confirmed that the transformation of the differential kinematics (Jacobian), as an example of the partial relationships, can be estimated by the proposed method.
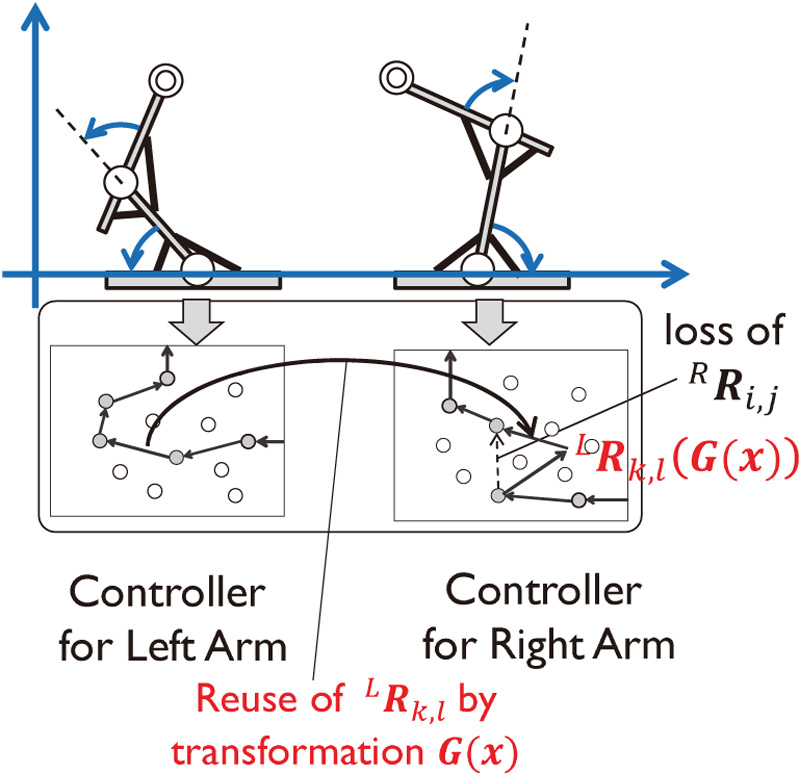
Transformation estimation to discover the reflection relation
- [1] L. P. Fried, C. M. Tangen, J. Walston, A. B. Newman, C. Hirsch, J. Gottdiener, T. Seeman, R. Tracy, W. J. Kop, G. Burke, and M. A. McBurnie, “Frailty in Older Adults: Evidence for a Phenotype,” The J. of Gerontology: Series A, Vol.56, No.3, pp. 146-157, 2001.
- [2] H. Eberle, Y. Hayashi, R. Kurazume, T. Takei, and Q. An, “Modeling of hyper-adaptability: from motor coordination to rehabilitation,” Advanced Robotics, Vol.35, No.13-14, pp. 802-817, 2021.
- [3] M. G. Perich, C. Arlt, S. Soares, M. E. Young, C. P. Mosher, J. Minxha, E. Carter, U. Rutishauser, P. H. Rudebeck, C. D. Harvey, and K. Rajan, “Inferring brain-wide interactions using data-constrained recurrent neural network models,” bioRxiv:2020.12.18.423348, 2020.
- [4] T. Isa, M. Mitsuhashi, and R. Yamaguchi, “Alternative routes for recovery of hand functions after corticospinal tract injury in primates and rodents,” Current Opinion in Neurology, Vol.6, No.5, pp. 836-843, 2019.
- [5] A. Ishida, K. Kobayashi, Y. Ueda, T. Shimizu, N. Tajiri, T. Isa, and H. Hida, “Dynamic Interaction between Cortico-Brainstem Pathways during Training-Induced Recovery in Stroke Model Rats,” The J. of Neuroscience, Vol.39, No.37, pp. 7306-7320, 2019.
- [6] M. Haruno, D. M. Wolpert, and M. Kawato, “MOSAIC model for sensorimotor learning and control,” Neural Computation, Vol.13, No.10, pp. 2201-2220, 2001.
- [7] K. Samejima, K. Doya, and M. Kawato, “MOSAIC Reinforcement Learning Architecture: Symbolization by Predictability and Mimic Learning by Symbol,” J. of the Robotics Society of Japan, Vol.19, No.5, pp. 551-556, 2001.
- [8] Y. Kobayashi, K. Harada, and K. Takagi, “Automatic Controller Generation Based on Dependency Network of Multi-modal Sensor Variables for Musculoskeletal Robotic Arm,” Robotics and Autonomous Systems, Vol.118, pp. 55-65, 2019.
- [9] Y. Kobayashi and S. Hosoe, “Planning-Space Shift Motion Generation: Variable-space Motion Planning Toward Flexible Extension of Body Schema,” J. of Intelligent and Robotic Systems, Vol.62, No.3-4, 2011.
- [10] T. Kohonen, “Self-Organizing Maps,” Springer, 2001.
- [11] Z. W. Luo and M. Ito, “Diffusion-based learning theory for organizing visuo-motor coordination,” Biological Cybernetics, Vol.79, No.4, pp. 279-289, 1998.
- [12] C. G. Atkeson, A. W. Moore, and S. Schaal, “Locally weighted learning for control,” Artificial Intelligence Review, Vol.11, No.1, pp. 75-113, 1997.
- [13] S. Umeyama, “Least-Squares Estimation of Transformation Parameters Between Two Point Patterns,” Trans. on Pattern Analysis and Machine Intelligence, Vol.13, No.4, pp. 376-380, 1991.
- [14] P. J. Besl and N. D. McKay, “A method for registration of 3-D shapes,” IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.14, No.2, pp. 239-256, 1992.
- [15] H. Masaki, S. Yoshihisa, K. Taku, and K. Tosiyasu, “Topology matching for fully automatic similarity estimation of 3D shapes,” The 49th Int. Conf. and Exhibition on Computer Graphics and Interactive Techniques, pp. 203-212, 2001.
- [16] E. K. P. Chong and S. H. Żak, “An Introduction to Optimization,” John Wiley & Sons, pp. 267-295, 2008.
- [17] K. Sims, “Evolving Virtual Creatures,” Proc. of the 21st annual Conf. on Computer Graphics and Interactive Techniques, pp. 15-22, 1994.
- [18] C. M. Fonseca and P. J. Fleming, “Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization,” the Fifth Int. Conf. on Genetic Algorithms, 1993.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.