Paper:
Physical Table Identification for Nominal Hydraulic Cylinders and its Application to Pressure Estimation
Satoru Sakai*, Kazuki Nagai**, and Yasuki Takahashi*
*Shinshu University
4-17-1 Wakasato, Nagano City, Nagano 380-8553, Japan
**Kubota Corporation
64 Ishizukita, Sakai-ku, Osaka 590-0823, Japan
The paper provides the first completed version of our identification approach as an intersection of two existing approaches: the physical model approach and the data table approach, for a set of valve flow blocks in nominal hydraulic cylinder dynamics. As one of the well-known physical models, the standard Bernoulli equation needs more accuracy in some cases owing to the steady flow assumption, whereas many data tables often need an expensive flow measurement. The proposed identification approach gives a new matrix representation that resembles the table representation but does not need any flow measurement as well as the steady flow assumption. In particular, unlike the conventional valve flow blocks, the updated valve flow blocks have no empty components via the projection guaranteeing the optimization. The effectiveness is confirmed experimentally by an application to the pressure estimation. The proposed identification approach will be applicable to other blocks including nonlinear friction blocks.
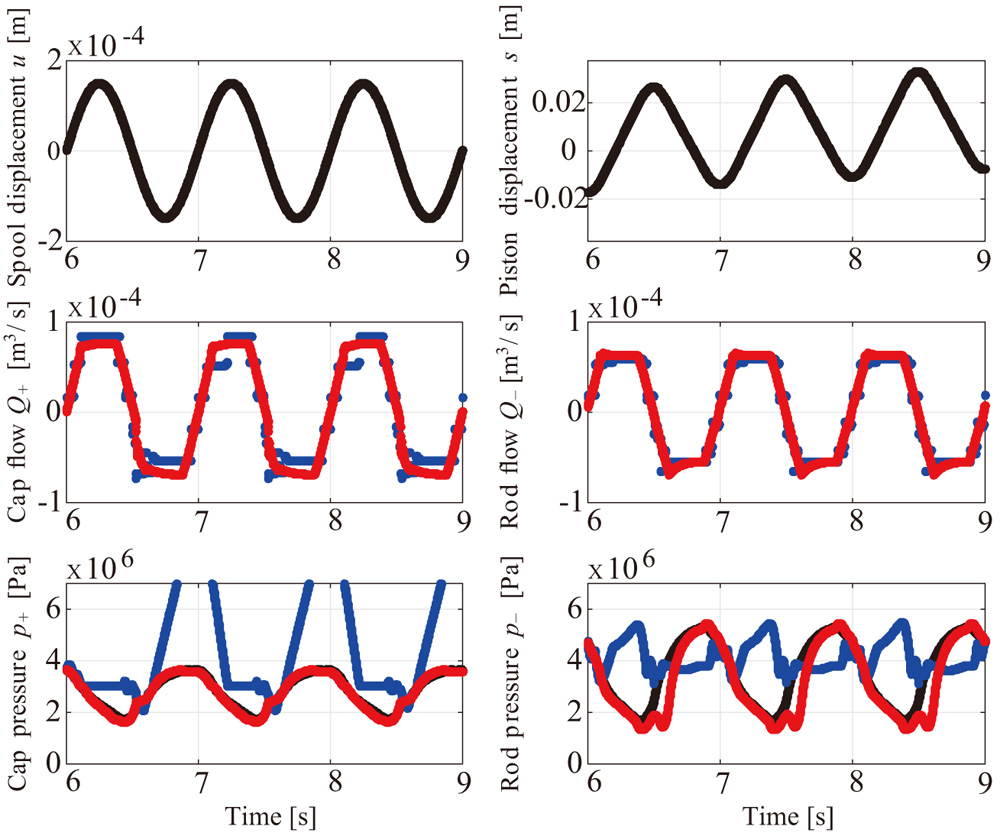
Proposed pressure to estimates the measured pressure against nonlinear dynamics
- [1] J. Mattila, J. Koivumaki, D. G. Caldwell, and C. Semini, “A Survey on Control of Hydraulic Robotic Manipulators with Projection to Future Trends,” IEEE/ASME Trans. on Mechatronics, Vol.22, No.2, pp. 669-680, 2017.
- [2] S. Sakai and S. Stramigioli, “Visualization of Hydraulic Cylinder Dynamics by a Structure Preserving Nondimensionalization,” IEEE/ASME Trans. on Mechatronics, Vol.23, No.5, pp. 2196-2206, 2018.
- [3] B. Heinrichs, N. Sepehri, and A. B. Thornton-Trump, “Position-based Impedance Control of an Industrial Hydraulic Manipulator,” IEEE Control Systems Magazine, Vol.17, No.1, pp. 46-52, 1997.
- [4] J. Watton, “Fluid Power Systems,” Prentice-Hall, 1989.
- [5] H. Merritt, “Hydraulic Control Systems,” John Willey and Sons, 1967.
- [6] M. Jelali and A. Kroll, “Hydraulic Servo Systems,” Springer, 2002.
- [7] A. Kugi and W. Kemmetmuller, “New Energy-based Nonlinear Controller for Hydraulic Piston Actuators,” European J. of Control, Vol.10, No.2, pp. 163-173, 2004.
- [8] T. Boaventura, M. Focchi, M. Frigerio, J. Buchli, C. Semini, G. A. Medrano-Cerda, and D. G. Caldwell, “On the Role of Load Motion Compensation in High-performance Force Control,” Proc. of 2012 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 4066-4071, 2012,
- [9] P. Y. Li and M. R. Wang, “Natural Storage Function for Passivity-Based Trajectory Control of Hydraulic Actuators,” IEEE/ASME Trans. on Mechatronics, Vol.19, No.3, pp. 1057-1068, 2014.
- [10] J. Yao, Z. Jiao, and D. Ma, “A Practical Nonlinear Adaptive Control of Hydraulic Servomechanisms with Periodic-like Disturbances,” IEEE/ASME Trans. on Mechatronics, Vol.20, No.6, pp. 2752-2760, 2015.
- [11] S. Sakai and Y. Maeshima, “A New Method for Parameter Identification for N-DOF Hydraulic Robots,” Proc. of 2014 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 5983-5989, 2014.
- [12] S. Summers, C. N. Jones, J. Lygeros, and M. Morari, “A Multiresolution Approximation Method for Fast Explicit Model Predictive Control,” IEEE Trans. of Automatic Control, Vol.56, No.11, pp. 2530-2541, 2011.
- [13] S. Sakai, K. Osuka, T. Maekawa, and M. Umeda, “Robust Control Systems of a Heavy Material Handling Agricultural Robot: A Case Study for Initial Cost Problem,” IEEE Trans. on Control Systems Technology, Vol.15, No.6, pp. 1038-1048, 2007.
- [14] M. P. Polverini, S. Formentin, L. Merzagora, and P. Rocco, “Mixed Data-Driven and Model-Based Robot Implicit Force Control: A Hierarchical Approach,” IEEE Trans. on Control Systems Technology, Vol.28, No.4, pp. 1258-1271, 2020.
- [15] S. Sakai and Y. Nabana, “Optimal Non-Bernoulli Modeling Method for Experimental Hydraulic Robots,” Proc. of 2016 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), pp. 2954-2959, 2016.
- [16] S. Sakai, Y. Nabana, and K. Nagai, “On-line Validation of the Unsteady Flow Blocks for Hydraulic Arm,” Trans. of JFPS, Vol.50, No.2, pp. 31-37, 2019 (in Japanese).
- [17] K. Zhou, J. C. Doyle, and K. Glover, “Robust and Optimal Control,” Prentice-Hall, 1996.
- [18] A. J. van der Schaft, “L2-Gain and Passivity Techniques in Nonlinear Control,” Springer-Verlag London, 2000.
- [19] T. Tsukiji, E. Noguchi, and F. Yoshida, “Development of oil hydraulic components using a flow visualization technique,” Int. J. Automation Technol., Vol.6, No.4, pp. 410-417, 2012.
- [20] D. G. Luenverger, “Optimization by Vector Space Method,” Wiley-Interscience, 1960.
- [21] S. Sakai, M. Ando, and S. Kobashi, “Visual Feedback without Geometric Features against Occlusion: A Walsh basis,” IEEE Trans. on Control Systems Technology, Vol.15, No.2, pp. 864-871, 2019.
- [22] L. Ljung, “System Identification: Theory for the User,” Prentice-Hall, 2nd edition, 1999.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.