Paper:
Flowrate Measurement in a Pipe Using Kalman-Filtering Laminar Flowmeter
Kazushi Sanada
Faculty of Engineering, Yokohama National University
79-5 Tokiwadai, Hodogaya, Yokohama, Kanagawa 240-8501, Japan
A laminar flowmeter that estimates the unsteady flowrate in a pipe using a Kalman filter is proposed. The laminar flowmeter has 32 narrow pipes. Kalman filtering is applied to one of the narrow pipes to estimate its flowrate. Three pressure sensors are connected to the narrow pipe. Upstream and downstream pressure signals are applied to a model of pipeline dynamics. The midpoint pressure is calculated and compared with the measured value. The error signal is fed back to the model. According to the principle of the Kalman filter, the estimated flowrate converges to the real flowrate. The Kalman-filtering estimation is conducted in a real-time computing system. In this study, the steady flowrate in a pipe is estimated and calibrated with measured data. The proposed Kalman-filtering-based laminar flowmeter demonstrates very promising performance.
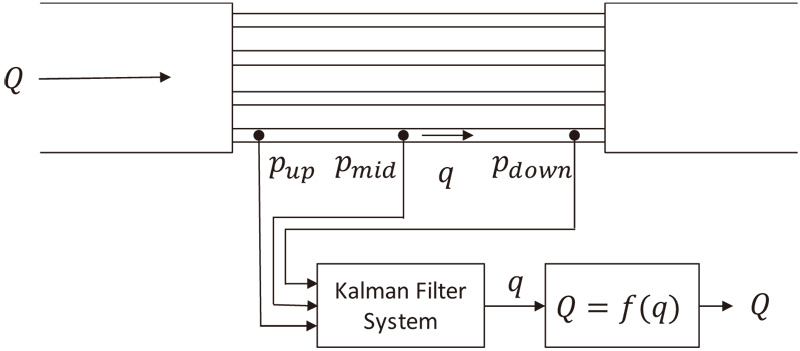
Kalman-filter-based laminar flowmeter
- [1] K. Sugimura and K. Suzuki, “Using Intermittently Operated Oil Hydraulic Pump Unit with Accumulator to Save Energy,” Int. J. Automation Technol., Vol.6, No.4, pp. 426-433, 2012.
- [2] P. Casoli, L. Riccò, F. Campanini, and A. Bedotti, “Hydraulic hybrid excavator–mathematical model validation and energy analysis,” Energies, Vol.9, No.12, 1002, 2016.
- [3] X. Lin, S. Pan, and D. Wang, “Dynamic simulation and optimal control strategy for a parallel hybrid hydraulic excavator,” J. of Zhejiang University SCIENCE A, Vol.9, No.5, pp.624-632, 2008.
- [4] T. Lin, Q. Wang, B. Hu, and W. Gong, “Research on the energy regeneration systems for hybrid hydraulic excavators,” Automation in Construction, Vol.19, No.8, pp. 1016-1026, 2010.
- [5] H. Kima, S. Yoob, S. Chob, and K. Yi, “Hybrid control algorithm for fuel consumption of a compound hybrid excavator,” Automation in Construction, Vol.68, pp. 1-10, 2016.
- [6] Y. Yua and K. Ahn, “Optimization of energy regeneration of hybrid hydraulic excavator boom system,” Energy Conversion and Management, Vol.183, pp. 26-34, 2019.
- [7] Q. Chena, T. Lina, H. Rena, and S. Fua, “Novel potential energy regeneration systems for hybrid hydraulic excavators,” Mathematics and Computers in Simulation, Vol.163, pp. 130-145, 2019.
- [8] N. Johnston, M. Pan, S. Kudzma, and P. Wang, “Use of Pipeline Wave Propagation Model for Measuring Unsteady Flow Rate,” J. of Fluids Engineering, Vol.136, No.3, 031203, 2014.
- [9] T. Zhao, K. Sanada, A. Kitagawa, and T. Takenaka, “Real Time Measurement for High Frequency Pulsating Flow Rate in a Pipe,” Trans. of the ASME, J. of Dynamic Systems, Measurement, and Control, Vol.112, No.4, pp. 762-768, 1990.
- [10] C. Shao, K. Xu, and Z. Shu, “Segmented Kalman filter based antistrong transient impact method for vortex flowmeter,” IEEE Trans. on Instrumentation and Measurement, Vol.66, Issue 1, pp. 93-103, 2017.
- [11] X. Huang, S. Yue, H. Zhang, and B. Sun, “The prediction of energy-saving electromagnetic flowmeter based on Kalman filtering method,” 2015 IEEE Int. Conf. on Applied Superconductivity and Electromagnetic Devices (ASEMD), pp. 262-263, 2015.
- [12] M. Akresh, W. D. Walker, and L. Reindl, “Flow measurement using Kalman filter for smoothing vortex shedding frequency,” Proc. of 2010 IEEE Instrumentation & Measurement Technology Conf., pp. 234-237, 2010.
- [13] A. Venugopal, A. Agrawal, and S. V. Prabhu, “Review on vortex flowmeter–Designer perspective,” Sensors and Actuators A, Vol.170, Issues 1-2, pp. 8-23, 2011.
- [14] A. Dadashnialehi and B. Moshiri, “Online monitoring of transit-time ultrasonic flowmeters based on fusion of optical observation,” Measurement, Vol.44, Issue 6, pp. 1028-1037, 2011.
- [15] X. Huang and S. Yue “The Energy-Saving Strategy of Electromagnetic Flowmeters Based on Various Predicting Methods,” IEEE Trans. on Applied Superconductivity, Vol.26, Issue 7, pp. 1-5, 2016.
- [16] C. Shao, K. Xu, and Z. Shu, “Segmented Kalman filter based antistrong transient impact method for vortex flowmeter,” IEEE Trans. on Instrumentation and Measurement, Vol.66, Issue 1, pp. 93-103, 2017.
- [17] X. Huang, S. Yue, H. Zhang, and B. Sun, “The prediction of energy-saving electromagnetic flowmeter based on Kalman filtering method,” 2015 IEEE Int. Conf. on Applied Superconductivity and Electromagnetic Devices (ASEMD), pp. 262-263, 2015.
- [18] S. Adachi and I. Maruta, “Fundamentals of Kalman Filter,” Tokyo Denki University Press, 2017 (in Japanese).
- [19] A. Ozawa, B. Gao, and K. Sanada, “Estimation of fluid transients in a pipe using Kalman filter based on optimized finite-element model,” SICE Annual Conf. 2010, pp. 1652-1657, 2010.
- [20] A. Ozawa and K. Sanada, “An indirect measurement method of transient pressure and flow rate in a pipe,” Proc. of the 8th Int. Symp. on Fluid Power, Okinawa 2011, pp. 104-109, 2011.
- [21] K. Sanada, “Using a Kalman filter to estimate unsteady flow,” Int. J. Automation Technol., Vol.6, No.4, pp. 440-444, 2012.
- [22] K. Sanada, “Simulation of Pipeline Dynamics Using an Optimized Finite Element Model,” J. Robot. Mechatron., Vol.11, No.4, pp. 283-288, 1999.
- [23] A. Ozawa and K. Sanada, “An indirect measurement method of transient pressure and flow rate in a pipe,” Proc. of the 8th Int. Symp. on Fluid Power, Okinawa 2011, pp. 104-109, 2011.
- [24] K. Sanada, “Using a Kalman filter to estimate unsteady flow,” Int. J. Automation Technol., Vol.6, No.4, pp. 440-444, 2012.
- [25] K. Sanada, C. W. Richards, D. K. Longmore, and D. N. Johnston, “A finite-element model of hydraulic pipelines using an optimized interlacing grid system,” Proc. of Institution of Mech Engineers, Part I: J. of Systems and Control Engineering, Vol.207, No.4, pp. 213-222, 1993.
- [26] W. Zielke, “Frequency-Dependent Friction in Transient Pipe Flow,” J. of Basic Engineering, Vol.90, No.1, pp. 109-115, 1968.
- [27] T. Kagawa, I. Lee, A. Kitagawa, and T. Takenaka, “High Speed and Accurate Computing Method of Frequency-Dependent Friction in Laminar Pipe Flow for Characteristics Method,” Trans. of the Japan Society of Mechanical Engineers (JSME), Series B, Vol.49, No.447, pp. 2638-2644, 1983.
- [28] D. N. Johnston and J. E. Drew, “Measurement of Positive Displacement Pump Flow Ripple and Impedance,” Proc. of Institution for Mechanical Engineers, Part I, Vol.210, No.1, pp. 65-74, 1996.
- [29] D. N. Johnston, “The Transmission Line Method for Modelling Laminar Flow of Liquid in Pipelines,” Proc. of Institution for Mechanical Engineers, Part I, Vol.226, No.5, pp. 586-597, 2012.
- [30] D. N. Johnston and K. A. Edge, “In Situ Measurement of the Wave speed and Bulk Modulus in Hydraulic Lines,” Proc. of Institution for Mechanical Engineers, Part I, Vol.205, No.3, pp. 191-197, 1991.
- [31] K. Sanada, “A study on order reduction of optimized finite-element model of pipeline dynamics,” Int. J. of Fluid Power System (JFPS), Vol.8, No.1, pp. 18-23, 2015.
- [32] K. Sanada, “Real-time implementation of Kalman filter for unsteady flow measurement in a pipe,” Int. J. of Hydromechatronics, Vol.1, No.1, pp. 3-15, 2018.
- [33] K. Sanada, “Condition for real-time measurement of power of unsteady fluid flow in a pipe by Kalman filter,” Proc. of 11th Int. Fluid Power Conf., pp. 178-185, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.