Paper:
Agreement Algorithm Based on a Trial and Error Method for the Best of Proportions Problem
Nhuhai Phung, Masao Kubo, and Hiroshi Sato
Department of Computer Science, National Defense Academy of Japan
1-10-20 Hashirimizu, Yokosuka, Kanagawa 239-8686, Japan
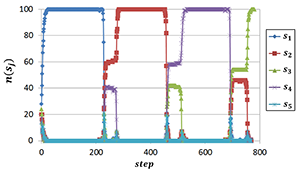
Dynamics of the decision making process
- [1] G. Valentini, E. Ferrante et al., “The Best-of-n Problem in Robot Swarms: Formalization, State of the Art, and Novel Perspectives,” Frontiers in Robotics and AI, Vol.4, pp. 1-18, 2017.
- [2] N. H. Phung, M. Kubo et al., “Agreement Algorithm with Trial and Error Method at Macro Level,” Artificial Life and Robotics, Vol.23, No.4, pp. 564-570, 2018.
- [3] N. H. Phung, M. Kubo et al., “El Farol Bar Problem by Agreement Algorithm based on Trial and Error Behavior at the Macro Lever,” Proc. of The 22nd Asia Pacific Symp. on Intelligent and Evolutionary Systems, 2018.
- [4] C. A. C. Parker and H. Zhang, “Cooperative Decision-Making in Decentralized Multiple-Robot Systems: the Best-of-n Problem,” IEEE/ASME Trans. on Mechatronics, Vol.14, Issue 2, pp. 240-251, 2009.
- [5] S. Iwanaga and A. Namatame, “The Complexity of Collective Decision,” Nonlinear Dynamics, Psychology, and Life Sciences, Vol.6, Issue 2, pp. 137-158, 2002.
- [6] J. Wessnitzer and C. Melhuish, “Collective Decision-Making and Behaviour Transitions in Distributed Ad Hoc Wireless Networks of Mobile Robots: Target-Hunting,” W. Banzhaf, J. Ziegler, T. Christaller, P. Dittrich, and J. T. Kim (Eds.), “Advances in Artificial Life. ECAL 2003. Lecture Notes in Computer Science,” Vol.2801, pp. 893-902, Springer, 2003.
- [7] G. Valentini, H. Hamann et al., “Self-Organized Collective Decision Making: The Weighted Voter Model,” Proc. of the 2014 Int. Conf. on Autonomous Agents and Multi-agent Systems, pp. 45-52, 2014.
- [8] T. D. Seeley, P. K. Visscher et al., “Stop Signals Provide Cross Inhibition in Collective Decision-Making by Honeybee Swarms,” Science, Vol.335, Issue 6064, pp. 108-111, 2012.
- [9] D. Pais, P. M. Hogan et al., “A Mechanism for Value-Sensitive Decision-Making,” PloS One, doi: 10.1371/journal.pone.0073216, 2013.
- [10] A. Reina, G. Valentini et al., “A Design Pattern for Decentralised Decision-Making,” PloS One, doi: 10.1371/journal.pone.0140950, 2015.
- [11] A. Reina, J. A. R. Marshall et al., “Model of the Best-of-N Nest-site Selection Process in Honeybees,” Phys. Rev. E, Vol.95, doi: 10.1103/PhysRevE.95.052411, 2017.
- [12] M. Kubo, N. H. Phung et al., “Efficient Collective Search by Agents that Remember Failures,” J. of Robotics, Networking and Artificial Life, Vol.5, No.1, pp. 67-70, 2018.
- [13] A. Scheidler, A. Brutschy et al., “The k-Unanimity Rule for Self-Organized Decision Making in Swarms of Robots,” IEEE Trans. on Cybernetics, Vol.46, Issue 4, pp. 1175-1188, 2016.
- [14] Y. Yang, C. Zhou et al., “Swarm Robots Task Allocation Based on Response Threshold Model,” Proc. of 4th Int. Conf. on Autonomous Robots and Agents, pp. 171-176, 2009.
- [15] Y. Yongming, C. Xihui et al., “Swarm Robots Task Allocation Based on Local Communication,” Proc. of 2010 Int. Conf. on Computer, Mechatronics, Control and Electronic Engineering, Vol.5, pp. 415-418, 2009.
- [16] E. Bonabeau, G. Theraulaz et al., “Fixed Response Thresholds and the Regulation of Division of Labor in Insect Societies,” Bulletin of Mathematical Biology, Vol.60, No.4 , pp. 753-807, 1998.
- [17] W. B. Arthur, “Inductive Reasoning and Bounded Rationality,” American Economic Review: Papers and Proc., Vol.84, No.2, pp. 404-411, 1994.
- [18] D. Whitehead, “The El Farol Bar Problem Revisited: Reinforcement Learning in a Potential Game,” ESE Discussion Papers 186, Edinburgh School of Economics, University of Edinburgh, 2008.
- [19] T. S. Schelling, “Micromotives and Macrobehavior,” W. W. Norton & Company, 1978.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.