Paper:
Uncertain Interval Data EFCM-ID Clustering Algorithm Based on Machine Learning
Yimin Mao*, Yinping Liu*, Muhammad Asim Khan*, Jiawei Wang*, Dinghui Mao**, and Jian Hu***
*Information Institute, Jiangxi University of Science and Technology
Hakka Avenue No.156, Zhanggong District, Ganzhou, Jiangxi 341000, China
**211 Battalion Co., Ltd., China Shanxi Nuclear Industry Group Company
Xi’an 710024, China
***Applied Science Institute, Jiangxi University of Science and Technology
Hakka Avenue No.156, Zhanggong District, Ganzhou, Jiangxi 341000, China
In clustering problems based on fuzzy c-means (FCM) for uncertain interval data, points within the interval are usually assumed to have uniform distribution, resulting in the difficulty of accurately describing the interval. Furthermore, the clustering results are considerably affected by the initial clustering centers, and the update speed of the membership degree is slow. To address these problems, a new clustering algorithm called uncertain FCM for interval data (EFCM-ID) is presented. On the basis of a quartile, a median quartile-spacing distance measurement for generally distributed interval data based on machine learning is designed to precisely determine these data. Simultaneously, we sample the whole dataset and consider the density centers as the initial clustering centers to increase accuracy. We call this method samplingbased density-center selection (SDCS). To reduce the running time, a new measurement based on competitive-learning theory to update the membership is developed. It accelerates the update speed by different degrees according to value of the membership degree. Experiments conducted on synthetic interval datasets show the feasibility of EFCM-ID.
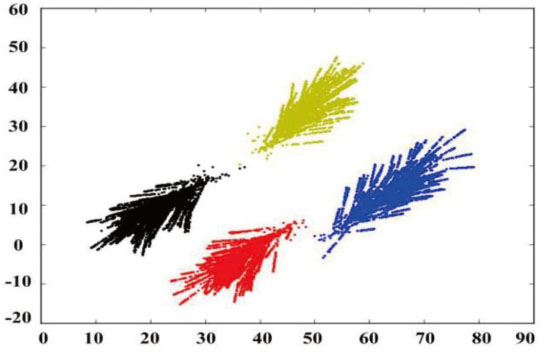
Data points in the skewed distribution
- [1] K. Zhao, S. Yang, S. Ding et al., “On cluster validation,” Systems Engineering – Theory and Practice, No.9, pp. 2417-2431, 2014.
- [2] H. Li, Y. Li, P. Zhao et al., “The subdivision of railway passenger transport market based on rough clustering algorithm,” J. of Transportation Systems Engineering and Information Technology, Vol.18, No.3, pp. 9-14, 2018.
- [3] R. A. Gevorgyan and Y. B. Hakobyan, “A matching based clustering algorithm for categorical data,” Computer Science, Vol.12, No.9, pp. 1-9, 2018.
- [4] K. Peng, V. C. M. Leung, and Q. Huang, “Clustering approach based on mini batch K-means for intrusion detection system over big data,” IEEE Access, Vol.6, No.99, pp. 11897-11906, 2018.
- [5] Y. Lu and C. Xia, “Optimized k-Nearest Neighbors and Local Density-Based Clustering Algorithm for Uncertain Data,” Control and Decision, Vol.31, No.3, pp. 541-546, 2016.
- [6] M. Faes, J. Cerneels, D. Vandepitte, and D. Moens, “Influence of measurement data metrics on the identification of interval fields for the representation of spatial variability in finite element models,” Pamm, Vol.16, No.1, pp. 27-30, 2016.
- [7] Y.-Y. Lee and D. Bhattacharya, “Applied welfare analysis for discrete choice with interval-data on income,” Social Science Electronic Publishing, Vol.23, No.8, pp. 1-14, 2018.
- [8] L. V. Utkin and Y. A. Zhuk, “An one-class classification support vector machine model by interval-valued training data,” Knowledge-based Systems, Vol.120, pp. 43-56, 2017.
- [9] Y. Ui, Y. Akiba, S. Sugano et al., “Excretion Detection System with Gas Sensor – Proposal and Verification of Algorithm Based on Time-Series Clustering –,” J. Robot. Mechatron., Vol.29, No.2, pp. 353-363, 2017.
- [10] C. Yu and Z. Fan, “A FCM clustering algorithm based on interval multiple index information,” Operations and Management, Vol.13, No.4, pp. 387-393, 2004.
- [11] X. Lianfeng and L. Weixiang, “A Extended FCM Clustering Algorithm Based on Interval Number,” Chemical Automation and Instrumentation, Vol.37, No.7, pp. 26-29, 2010.
- [12] P. D’Urso, R. Massari, L. D. Giovanni, and C. Cappelli, “Exponential distance-based fuzzy clustering for interval-valued data,” Fuzzy Optimization and Decision Making, Vol.16, No.1, pp. 51-70, 2017.
- [13] S. Wei, F. D. Salim, A. Song, and A. Bouguettaya, “Clustering big spatiotemporal-interval data,” IEEE Trans. on Big Data, Vol.2, No.3, pp. 190-203, 2016.
- [14] D. Guido, N. Marotta, G. Morsella, and L. Suriano, “A Gromov-Hausdorff distance between von Neumann algebras and an application to free quantum fields,” J. of Functional Analysis, Vol.272, No.8, pp. 3238-3258, 2017.
- [15] G. Junpeng, T. Zhihui, and D. Deng, “Systematic cluster analysis of interval data based on Hausdorff distance,” Mathematical Statistics and Management, Vol.33, No.4, pp. 634-641, 2014.
- [16] L. Xianling, W. Hongbin, and X. Xian, “Human Behavior Recognition Based on Acceleration Signal and Evolutionary RBF Neural Network,” Pattern Recognition and Artificial Intelligence, Vol.28, No.12, pp. 1127-1136, 2015.
- [17] S. Akimoto, T. Takahashi, M. Suzuki et al., “Human detection by Fourier descriptors and fuzzy color histograms with fuzzy c-means Method,” J. Robot Mechatron, Vol.28, No.4, pp. 491-499, 2016.
- [18] T. Lei, X. Jia, Y. Zhang, et al., “Significantly fast and robust fuzzy c-means clustering algorithm based on morphological reconstruction and membership filtering,” IEEE Trans. on Fuzzy Systems, Vol.26, No.5, pp. 3027-3041, 2018.
- [19] L. Chunsheng and W. Yaonang, “New Method of Initialization of Clustering Centers,” Control Theory and Applications, Vol.27, No.9, pp. 1435-1440, 2010.
- [20] G. Junpeng, W. Weili, and L. Minglu, “SOM clustering method for general distribution of interval symbolic data,” Mathematical Statistics and Management, Vol.35, No.6, pp. 1002-1015, 2016.
- [21] F. de A. T. de Carvalho, R. M. C. R. de Souza, M. Chavent et al., “Adaptive Hausdorff distances and dynamic clustering of symbolic interval data,” Pattern Recognition Letters, Vol.27, No.3, pp. 167-179, 2006.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.