Paper:
Design of a Flexibly-Constrained Revolute Pair with Non-Linear Stiffness for Safe Robot Mechanisms
Naoto Kimura, Nobuyuki Iwatsuki, and Ikuma Ikeda
Department of Mechanical Engineering, School of Engineering, Tokyo Institute of Technology
2-12-1 Ookayama Meguro-ku, Tokyo 152-8552, Japan
A revolute pair with a flexible translational constraint on a plane is proposed as simple mechanism for safe robots. The mechanism is composed of two pairing elements, one with a circular and one with a cam profile that are connected by a linear spring. Flexible translational constraint is generated by spring forces and the reaction force between the two pairing elements. Two methods for designing the cam profile are proposed in order to implement the specified non-linear stiffness in the flexible constraint. Design examples with various stiffness characteristics are shown. Some prototypes are fabricated, and it is confirmed that they perform as designed. As an application, a flexible, underactuated link mechanism with the proposed pairs is synthesized, and its flexibility and kinematic performance are investigated.
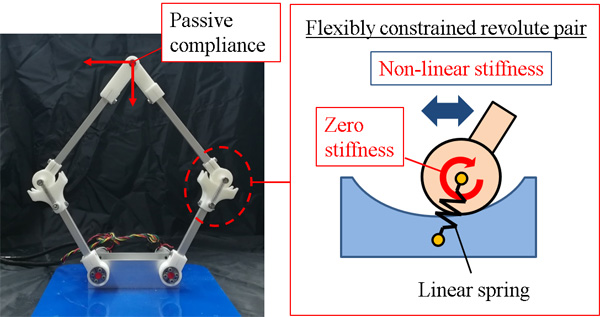
Flexible linkage with the proposed kinematic pairs
- [1] J. K. Salisbury, “Active Stiffness Control of a Manipulator in Cartesian Coordinates,” Proc. of the 19th IEEE Conf. on Decision and Control, Vol.19, pp. 95-100, doi: 10.1109/CDC.1980.272026, 1980.
- [2] N. Hogan, “Impedance Control: An Approach to Manipulation: Part 1-3,” J. of Dynamic Systems, Measurement, and Control, Vol.107, pp. 1-24, doi: 10.1115/1.3140702, 1985.
- [3] K. F. Laurin-Kovitz, E. Colgate, and S. D. R. Carnes, “Design of Components for Programmable Passive Impedance,” Proc. of the 1991 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 1476-1481, doi: 10.1109/ROBOT.1991.131824, 1991.
- [4] G. Tonietti, R. Schiavi, and A. Bicchi, “Design and Control of a Variable Stiffness Actuator for Safe and Fast Physical Human/Robot Interaction,” Proc. of the 2005 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 526-531, doi: 10.1109/ROBOT.2005.1570172, 2005.
- [5] S. A. Migliore, E. A. Brown, and S. P. De Weerth, “Biologically Inspired Joint Stiffness Control,” Proc. of the 2005 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 4508-4513, doi: 10.1109/ROBOT.2005.1570814, 2005.
- [6] G. Palli et al., “Design of a Variable Stiffness Actuator Based on Flexures,” J. of Mechanisms and Robotics, Vol.3, No.3, 034501, doi: 10.1115/1.4004228, 2011.
- [7] Y. Hayashibara, “Study on a Variable Stiffness Mechanism Using Wire Spring,” J. Robot. Mechatron., Vol.20, No.2, pp. 296-301, doi: 10.20965/jrm.2008.p0296, 2008.
- [8] B.-S. Kim and J.-B. Song, “Hybrid Dual Actuator Unit: A Design of a Variable Stiffness Actuator based on an Adjustable Moment Arm Mechanism,” Proc. of the 2010 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 1655-1660, doi: 10.1109/ROBOT.2010.5509264, 2010.
- [9] A. Jafali et al. “A New Actuator With Adjustable Stiffness Based on a Variable Ratio Lever Mechanism,” IEEE/ASME Trans. on Mechatronics, Vol.19, No.1, pp. 55-63, doi: 10.1109/TMECH.2012.2218615, 2014.
- [10] S. Wolf and G. Hirzinger, “A New Variable Stiffness Design: Matching Requirements of the Next Robot Generation,” Proc. of the 2008 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 1741-1746, doi: 10.1109/ROBOT.2008.4543452, 2008.
- [11] S. Wolf, O. Eiberger, and G. Hirzinger, “The DLR FSJ: Energy based design of a variable stiffness joint,” Proc. of the 2011 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 5082-5089, doi: 10.1109/ICRA.2011.5980303, 2011.
- [12] J.-J. Park and J.-B. Song, “A Nonlinear Stiffness Safe Joint Mechanism Design for Human Robot Interaction,” J. of Mechanical Design, Vol.132, No.6, 061005, doi: 10.1115/1.4001666, 2010.
- [13] H. J. Bidgory, M. N. Ahmadabadi, and M. R. Zakerzadeh, “Design and Modeling of a Compact Rotational Nonlinear Spring,” Proc. of the 2016 IEEE Int. Conf. on Intelligent Robots and Systems (IROS), pp. 4356-4361, doi: 10.1109/IROS.2016.7759641, 2016.
- [14] H. O. Lim, K. Maenisi, and M. Sunagawa, “Development of Collision Force Suppression Mechanism,” Proc. of the 2008 IEEE Int. Conf. on Control, Automation and Systems, pp. 2032-2037, doi: 10.1109/ICCAS.2008.4694463, 2008.
- [15] D. Accoto, et al., “pVEJ: a Modular Passive Viscoelastic Joint for Assistive Wearable Robots,” Proc. of the 2012 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3361-3366, doi: 10.1109/ICRA.2012.6225167, 2012.
- [16] S. Lan and Z. Song, “Design of a New Nonlinear Stiffness Compliant Actuator and Its Error Compensation Method,” J. of Robotics, Vol.2016, 7326905, doi: 10.1155/2016/7326905, 2016.
- [17] N. Kashiri, D. G. Caldwell, and N. Tsagarakis, “A Self-adaptive Variable Impedance Actuator Based on Intrinsic Non-linear Compliance and Damping Principles,” Proc. of the 2017 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 1248-1254, doi: 10.1109/ICRA.2017.7989148, 2017.
- [18] S. Nicolas and M. Okada, “Synthesis of a Non-circular Cable Spool to Realize a Non-linear Rotational Spring,” Proc. of the 2011 IEEE Int. Conf. on Intelligent Robots and Systems (IROS), pp. 762-767, doi: 10.1109/IROS.2011.6094545, 2011.
- [19] A. Schepelmann, K. A. Geberth, and H. Geyer, “Compact Nonlinear Springs with User Defined Torque-Deflection Profiles for Series Elastic Actuators,” Proc. of the 2014 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 3411-3416, doi: 10.1109/ICRA.2014.6907350, 2014.
- [20] B. Kim and A. D. Deshpande, “Design of Nonlinear Rotational Stiffness Using a Non-circular Pulley-spring Mechanism,” J. of Mechanisms and Robotics, Vol.6, No.4, 041109, doi: 10.1115/1.4027513, 2014.
- [21] P.-H. Kuo and A. D. Deshpande, “A Novel Joint Design for Robotic Hands With Humanlike Nonlinear Compliance,” J. of Mechanisms and Robotics, Vol.8, No.2, 021004, doi: 10.1115/1.4031300, 2016.
- [22] M. Okada and S. Kino, “Torque Transmission Mechanism with Nonlinear Passive Stiffness using Mechanical Singularity,” Proc. of the 2008 IEEE Int. Conf. on Robotics and Automation (ICRA), pp. 1735-1740, doi: 10.1109/ROBOT.2008.4543451, 2008.
- [23] N. Iwatsuki and N. Terashima, “Flexibility Control of Redundant Closed-loop Mechanisms with Elastic Elements,” Proc. of the 1st IFToMM Asian Conf. on Mechanism and Machine Science, pp. 210-215, 2010.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.