Paper:
Sliding Mode Control for Vibration Comfort Improvement of a 7-DOF Nonlinear Active Vehicle Suspension Model
Zhiyong Yang*1, Shan Liang*2, Yu Zhou*3, and Di Zhao*4
*1Department of Information Engineering, Chongqing Vocational Institute of Engineering
No.1 North-South Avenue, Jiangjin, Chongqing 402260, China
*2College of Automation, Chongqing University
No.174 Shazhengjie, Shapingba, Chongqing 400044, China
*3Department of Finance and Trade, Chongqing Vocational Institute of Engineering
No.1 North-South Avenue, Jiangjin, Chongqing 402260, China
*4School of Electronic Engineering, Beijing University of Posts and Telecommunications
No.10 Xitucheng Road, Haidian District, Beijing 100876, China
Owing to the presence of nonlinear elements of a vehicle, when the vehicle goes through a rough-road-surface, such as consecutive speed control humps (SCHs), unexpected vibrations will exist in vehicle suspension systems, such as chaos, bifurcation, and quasi-periodic so on. In this paper, we first study the possibility of chaotic vibration of the seven degree-of-freedom (7-DOF) full vehicle model under consecutive SCHs on the highway. Then, a non-chattering sliding mode control method is proposed. The effectiveness of the sliding mode control method for the nonlinear vibration control of the vehicle suspension model is verified by numerical simulation. By comparing the changes in the vibration amplitude of the vehicle in the same velocity region before and after the control, we determine whether the ride comfort is improved. The results show that not only is the system’s chaos vibration effectively controlled, but also the ride comfort is significantly improved. The results can be applied in the design of a vehicle and in pavement of road humps.
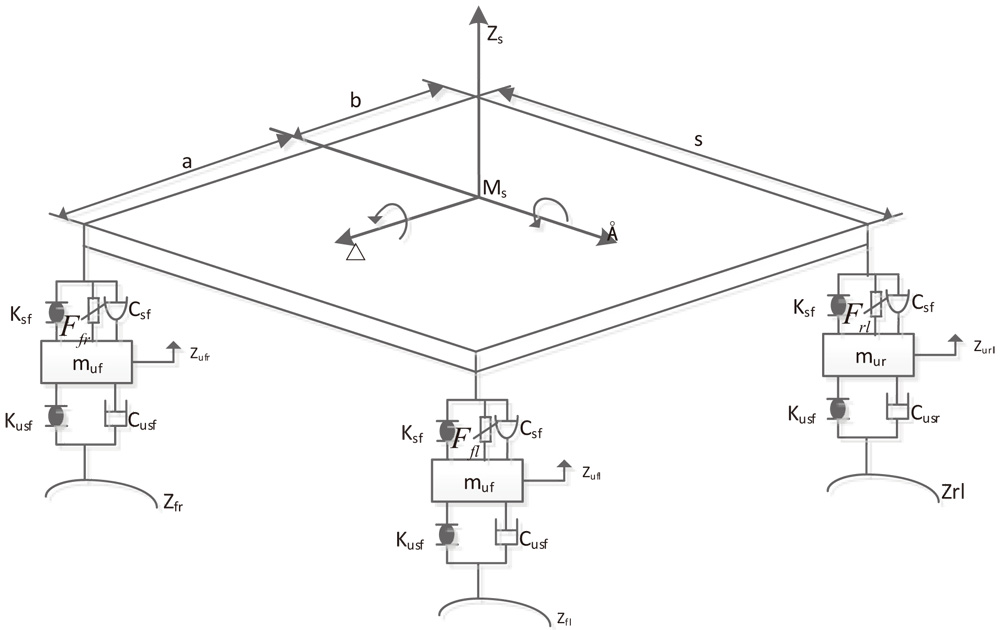
Non-linear 7-DOF full-vehicle model
- [1] S. Zuo and P. S. Zhang, “Energy harvesting, ride comfort, and road handling of regenerative vehicle suspensions,” J. of Vibration and Acoustics, Vol.135, No.1, pp. 1-7, 2013.
- [2] Z. Y. Yang, S. Lang, Y. S. Sun et al., “Vibration suppression of four degree-of-freedom nonlinear vehicle suspension model excited by the consecutive speed humps,” J. of Vibration and Control, Vol.22, No.6, pp. 1560-1567, 2016.
- [3] S. Liang, C. G. Li, and Q. Zhu, “The Influence of the consecutive speed control humps parameters on the chaotic vibration of a 2 DOF nonlinear vehicle,” J. of Vibroengineering, Vol.13, No.3, pp. 406-413, 2011.
- [4] S. Liang, Y. S. Sun, Q. Zhu, and Z. Y. Yang, “Ride comfort analysis of a nonlinear vehicle excited by the consecutive speed-control humps,” J. of Vibroengineering, Vol.15, No.49, pp. 1656-1664, 2013.
- [5] F. Liu, S. Liang, and Q. Zhu, “Effects of the consecutive speed humps on chaotic vibration of a nonlinear vehicle model,” J. of ICIC Express Letters, Vol.4, No.49, pp. 1657-1664, 2010.
- [6] Q. Zhu and S. Liang, “A method for detecting chaotic vibration based on continuous wavelet transform,” Int. J. of Sensing, Computing & Control, Vol.1, No.2, pp. 125-132, 2011.
- [7] Z. Y. Yang, S. Liang, and Q. Zhu, “Chaotic vibration and comfort analysis of nonlinear full-vehicle model excited by consecutive speed control humps,” J. of Mathematical Problems in Engineering, Vol.2014, pp. 1-8, 2014.
- [8] H. Bayrannoglu and H. Komurcugil, “Nonsingular decoupled terminal sliding-mode control for a class of four-order nonlinear system,” J. of Commun. Nonlinear Sci. Numer. Simulat., Vol.18, No.7, pp. 2527-2539, 2013.
- [9] Z. Y. Yang, S. Liang, Q. Zhu et al., “Chaotic vibration and control in nonlinear half-vehicle suspension under consecutive speed-control humps excitation,” J. Robot. Mechatron., Vol.27, No.5, pp. 513-519, 2015.
- [10] A. A. Aldair and W. J. Wang, “A neurofuzzy controller for full vehicle suspension systems,” J. of Vibration and Control, Vol.18, No.12, pp. 1837-1854, 2012.
- [11] J. Zheng, S. Liang, Q. Zhu et al., “Chaotic vibration of vehicle suspension excited by consecutive speed control hump,” J. of Highway and Transportation Research and Development, Vol.28, No.1, pp. 132-137, 2011.
- [12] Z. Y. Yang, S. Liang et al., “Research and chaotic vibration characteristics of nonlinear half vehicle model under quasi-periodic excitation,” J. of Zhengzhou University Engineering Science, Vol.36, No.1, pp. 110-118, 2015.
- [13] Z. Y. Yang, Y. Zhou, and S. Liang, “Sliding mode control of chaos vibrations in 7-DOF nonlinear active vehicle suspension,” IEEE Int. Conf. on Advanced Mechatronic Systems, pp. 467-471, 2017.
- [14] Y. F. Yang, X. M. Ren, and W. Y. Qin, “Description Nonlinear Responses Using Peak-to-peak Values,” J. of China Mechanical Engineering, Vol.16, No.16, pp. 1468-1470, 2005.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.