Paper:
Utilizing the Nonlinearity of Tendon Elasticity for Compensation of Unknown Gravity of Payload
Chao Shao*, Junki Togashi**, Kazuhisa Mitobe*, and Genci Capi***
*Department of Mechanical Systems Engineering, Yamagata University
4-3-16 Yonezawa, Yamagata 992-8510, Japan
**Kumagaigumi Co., Ltd.
1043 Onigakubo, Tsukuba 300-2651, Japan
***Department of Mechanical Engineering, Hosei University
3-7-2 Kajinocho, Koganei, Tokyo 184-8584, Japan
This paper discusses the positioning control of an elastic tendon-driven robot arm under gravity. The robot is driven by rubber string tendons and winding drums attached on the outside frames. Low-cost rubber strings that are available commercially are used as tendons. The goal is to utilize the nonlinear nature of the rubber materials to control a low-cost and soft robot arm. Theoretically, a mathematical model with accurate parameters and accurate measurement of the payload weight is necessary for rigorous gravity compensation. However, the necessity for the information of the robot parameters is hindering easy adaptability, versatility, and cost-efficiency. This paper presents an iterative estimation and compensation method for unknown payloads based on the steady-state position error and the nominal stiffness coefficient. Owing to the nonlinearity of the actual rubber strings, the position error remains after a single operation of the gravity compensation. However, experiments indicate that the error reduces by a simple iteration of the same compensation operation. Considering the nonlinearity in rubber strings, the mechanism of the error reduction is analyzed theoretically. Although the iterative process is time consuming, the method requires less prior information. In addition, it is cost effective because a sophisticated force sensor is not required. As the mechanism of error reduction applies to typical rubber string materials, it is useful for significant cost-reduction and reconfigurable robotics.
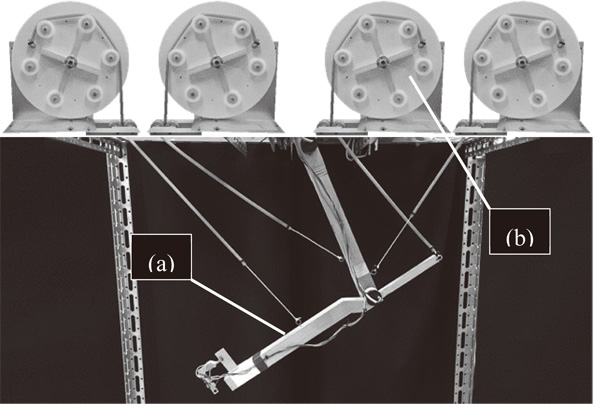
Winding drums for elastic tendon robot
- [1] Y. Xu and R. P. Paul, “A robot compliant wrist system for automated assembly,” IEEE Int. Conf. on Robotics and Automation, Vol.3, pp. 1750-1755, 1990.
- [2] K. Koganezawa, H. Inomata, and T. Nakazawa, “Actuator with non-linear elastic system and its application to 3 DOF wrist joint,” Int. Conf. on Mechatronics and Automation, Vol.3, pp. 1253-1260, 2005.
- [3] N. Saga, J. Nagase, and Y. Kondo, “Development of a Tendon- Driven System Using a Pneumatic Balloon,” J. Robot. Mechatron., Vol.18, No.2, pp. 139-145, 2006.
- [4] M. T. Mason, “Compliance and Force Control for Computer Controlled Manipulators,” IEEE Trans. on Systems, Man and Cybernetics, Vol.11, Issue 6, pp. 418-432, 1981.
- [5] B. J. Waibel and H. Kazerooni, “Theory and Experiments on the Stability of Robot Compliance Control,” IEEE Trans. on Robotics and Automation, Vol.7, No.1, pp. 95-104, 1991.
- [6] M. H. Raibert and J. J. Craig, “Hybrid Position/Force Control of Manipulators,” ASME J. of Dynamic Systems, Measurement, and Control, Vol.103, No.2, pp. 126-133, 1981.
- [7] G. K. Klute, J. M. Czerniecki, and B. Hannaford, “McKibben artificial muscles: pneumatic actuators with biomechanical intelligence,” Proc. Int. Conf. on Advanced Intelligent Mechatronics, pp. 221-226, 1999.
- [8] B. Tondu and P. Lopez, “Modeling and control of McKibben Artificial Muscle Robot Actuators,” IEEE Control Systems Magazine, pp. 15-38, 2000.
- [9] T. Noritsugu, M. Kubota, and S. Yoshimatsu, “Development of Pneumatic Rotary Soft Actuator Made of Silicone Rubber,” J. Robot. Mechatron., Vol.13, No.1, pp. 17-22, 2001.
- [10] G. Tonietti, R. Schiavi, and A. Bicchi, “Design and control of a variable stiffness actuator for safe and fast physical human/robot inter- action,” Int. Conf. on Robotics and Automation (ICRA), pp. 526-531, 2005.
- [11] K. Koganezawa, Y. Watanabe, and N. Shimizu, “Antagonistic muscle-like actuator and its application to multi-d.o.f. forearm pros-thesis,” Advanced Robotics, Vol.12, Nos.7-8, pp. 771-789, 1997.
- [12] G. A. Pratt and M. M. Williamson, “Series elastic actuators,” Int. Conf. on Intelligent Robots and Systems, Vol.1, pp. 399-406, 1995.
- [13] N. Hogan, “Impedance Control: An Approach to Manipulation: Part II – Implementation,” ASME, J. Dyn. Sys. Meas. Control, Vol.107, No.1, pp. 8-16, 1985.
- [14] T. Tsuji, “Human Arm Impedance in Multi-Joint Movements,” P. G. Morasso and V. Sanguineti (Eds.), “Self-Organization, Computational Maps, and Motor Control,” Elsevier, pp. 357-380, 1997.
- [15] J. Togahsi, K. Mitobe, and G. Capi, “Control of Low-Cost Customizable Robot Arm Actuated by Elastic Tendons,” J. Robot. Mechatron., Vol.28, No.4, pp. 509-522, 2016.
- [16] T. Lens and O. von Stryk, “Investigation of Safety in Human-Robot-Interaction for a Series Elastic, Tendon-Driven Robot Arm,” Int. Conf. on Intelligent Robots and Systems (IROS), pp. 4309-4314, 2012.
- [17] T. Lens and O. von Stryk, “Design and Dynamics Model of a Lightweight Series Elastic Tendon-Driven Robot Arm,” IEEE Int. Conf. on Robotics and Automation (ICRA), Karlsruhe, pp. 4512-4518, May 6-10, 2013.
- [18] H. Kobayashi, K. Hyodo, and D. Ogane, “On Tendon-Driven Robotic Mechanisms with Redundant Tendons,” Int. J. of Robotics Research, Vol.17, No.5, pp. 561-571, 1998.
- [19] H. Aschemann and D. Schindele, “Comparison of model-based approaches to the compensation of hysteresis in the force characteristic of pneumatic muscles,” IEEE Trans. Ind. Electron., Vol.61, pp. 3620-3629, 2014.
- [20] C. J. Lin, C. R. Lin, S. K. Yu, and C. T. Chen, “Hysteresis modeling and tracking control for a dual pneumatic artificial muscle system using Prandtl-Ishlinskii model,” Mechatronics, Vol.28, pp. 35-45, 2015.
- [21] S. L. Xie, H. T. Liu, J. P. Mei, and G. Y. Gu, “Modeling and compensation of asymmetric hysteresis for pneumatic artificial muscles with a modified generalized Prandtl-Ishlinskii model,” Mechatronics, Vol.52, pp. 49-57, 2018.
- [22] C. Song, S. Q. Xie, Z. Zhou, and Y. Hu, “Modeling of pneumatic artificial muscle using a hybrid artificial neural network approach,” Mechatronics, Vol.31, pp. 124-131, 2015.
- [23] S. Arimoto, “Control Theory of Nonlinear Mechanical Systems: A Passivity-based and Circuit-theoretic Approach,” Clarendon Press Oxford, pp. 174-176, 1996.
- [24] R. M. Murray, Z. Li, and S. Sastry, “A Mathematical Introduction to Robotic Manipulation,” CRC Press, 1994.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.